Part III: Selecting the final network
Editor's note: Robert Brass is president and co-founder of Development II Inc., a Woodbury, Conn., research firm.
This is the final article in a three-part series describing the use of neural networks for analyzing a survey. The previous two segments were published in the June and July/August issues of Quirk's Marketing Research Review. The focus of this serialized article was to present a "cookbook" approach for using an extremely powerful tool to define the decision process of respondents to a survey. Sprinkled between the various rules of thumb and process descriptions are periodic discussions of the theory.
In order to gain the most from this final article it is important to have read the second installment (the July/August issue). In fact, it is not a bad idea to have it conveniently available for reference. While there will be some review of the highlights of the previous installments, it will not cover all key aspects of the prior discussions.
As previously defined, the goal of this particular analysis was to determine the most effective actions that can be taken to create Totally Satisfied customers from those who weren't Totally Satisfied with the results of a service call to repair their computer. Since there were only a very small group of Dissatisfied customers the focus of the analysis is exclusively on the Somewhat Satisfied customer group.
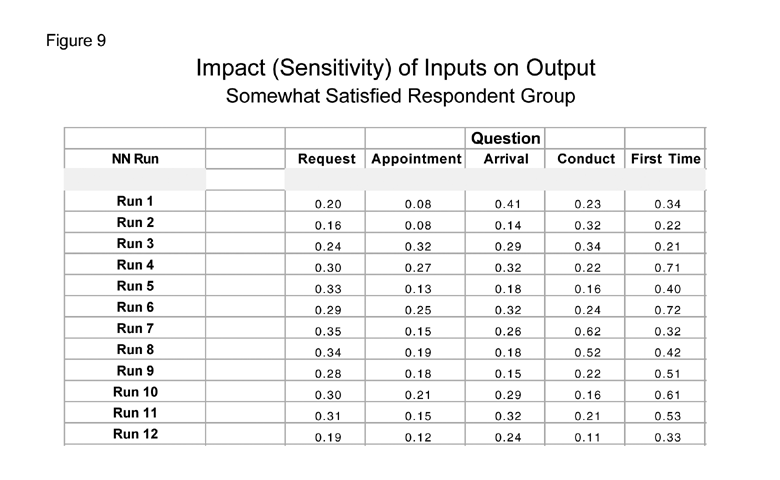
In the previous installment the sensitivity of the five selected inputs was tabulated for each of 12 different neural networks (Figure 9). This table describes the impact that each input has on the output of the neural network for the group of customers who were Somewhat Satisfied with the service call. A table with the same format and associated contents is usually also developed for the Totally Satisfied and for the Dissatisfied customer group. In the example used in this article, the Somewhat Satisfied customer group is the most critical and will be the sole basis of the discussion.
 |
Figure 9 documents the results of 12 different neural networks derived from the same survey data. Each entry in that table describes the change in the output (Overall Satisfaction) to a corresponding change in the input. For example, in Run 1, if the satisfaction level of the input "Arrival" increased by 1 percent and all other inputs remain unchanged, the Overall Satisfaction would increase by .41 percent. By examining the sensitivity of the five inputs in all of the 12 networks, it is apparent that there are very different conclusions that could be drawn, depending upon the choice of the network. The primary goal of this final discussion is to describe the process that can be used to identify the specific network that is most representative of the survey respondents decision process.
The pervasive theme in this series of articles is that when a neural network is used to analyze a survey with a limited number of respondents there will be major variations among neural networks derived from the respondent data. The underlying cause of this problem is twofold:
First, there are usually only several hundred surveys that document the results of a market research program. To effectively develop a neural network, the survey data must be split between two groups, one group to train the network and the other to test it. In many cases, this split is approximately equal. This obviously can create a bias, so to minimize the impact of the small groups, the training/testing process is repeated many times with a new randomization of the split between the training and testing survey data.
Second, the order of the surveys used for training a neural network, the architecture of the neural network (the number of neurons in the hidden layers) and the training strategies all interact to produce different networks. While all of the optimally trained networks may give approximately the same statistical accuracy in developing outputs corresponding to similar input sets, the sensitivities of any single input can vary significantly.
The key then is to have a process by which the neural network that most represents the decision logic of the survey respondents is identified. This is the primary subject of this final installment.
Selecting the "runs" to populate the impact table
Figure 9 contains the results of 12 trained networks. This is used for illustrating the process. In the best of all possible worlds, instead of 12 alternatives to choose from there would be 50 to 100 or more. With an increasing number of choices, the process that will be described for calculating the quantitative relationships becomes potentially more accurate. However, as will become somewhat apparent with further discussion, the identification of the one or two most sensitive inputs can almost always be characterized even with a limited number of choices.
Part II of this article (July/August issue) presented the table in Figure 9 without discussing the method used for selecting the specific runs that were chosen to populate it. The process is quite straightforward. Each of the randomizations of the respondent data, split between training and testing, develops about 700 separate networks. Each individual network is defined when the progress of training is suspended and the current state of the neural network is statistically tested. Each of these tested alternative networks then is examined with the goal of selecting those that could potentially be the "Most Representative" network.
There are three important statistics that are available for each neural network.
1. The average error between the predicted output and the actual output.
2. The RMS (root mean square) between the predicted output and the actual output.
3. R2 (a measure of the amount of change in the output that is predictable by the changes in the input).
In order to be precise in the definition, the R2 calculated using the results of the neural network is an approximation and not exactly equivalent to that terminology as used in formal statistics. It is, however, a reasonable alternative.
The selections of the specific runs (1-12) that populate this table follow a very simple rule of thumb. All selected runs must have been derived with at least 60 cycles of training. That is, the training deck must have been completely examined at least 60 times. Then, three networks are selected from the alternatives derived from each randomization of the survey data.
- First select the run with the highest R2.
- Second, select a different run with the lowest average error. However, the architecture of this network must be different than the one already associated with the highest R2 selection.
- Third and finally, select a third alternative with the lowest RMS error but with the similar restriction that the architecture must be different from the network selected for the optimum average error or R2.
The bottom line is that each of survey data randomizations, which develop 700 tested networks, contributes a maximum of three networks. Therefore, the table in Figure 9 consists of the best three choices from each of four randomizations of the survey data. While it is possible to select more than three networks from each randomization, the similarities that would exist among some of the networks would detract from the value of increasing the number of choices.
How do you select the most representative network?
As a basis for explaining the process, let us abandon reality and slip into the ideal world. Assume that we do have a table with 100 potential "Most Representative" networks. How do you find that needle in the haystack? Just as a survey uses a sample to predict the opinions of the "universe," the same philosophy for identifying central tendencies could be used to formulate the process for the "Most Representative" selection.
Often survey data is segmented to create a small number of groups that share common characteristics. The goal of this type of analysis is to characterize each group separately to identify and classify their uniqueness. Since we are dealing with the world of neural networks, there is a methodology called Kohonen network analysis that will do exactly that. It basically can divide survey information into a small number of segments that share similar characteristics. Usually there is one dominant group and a few smaller alternates. If the central tendencies of the characteristics (in this case the sensitivities of the inputs to the outputs) of the dominant group are identified, this would be a reasonable choice for of the "Most Representative" network.
Reality, on the other hand, presents us with 12 networks and using Kohonen or another sophisticated segmentation program would certainly be overkill. As a substitute, we offer the following simple process.
The process to identify the most representative neural network
The overall strategy is to graphically segment the data by highlighting key factors. The first step is to identify the highest two sensitivities in each of the runs. In Figure 10, the highest is outlined in bold and tinted with gray. The second highest is outlined only. As is obvious, a pattern has now emerged.
 |
The second step is to eliminate those runs that are at odds with the largest group. Figure 11 displays the now reduced table. Runs 2, 3, 7 and 8 were eliminated. There is a reasonable argument to either toss out Run 1 or keep it, so for interest it was retained. The average of the remaining runs was then derived and is listed in the bottom of Figure 11.
 |
This set of averages could be used by itself as the representative sensitivities, however it is more helpful to identify the run that is most similar to those averages. Having a working neural network instead of abstract averages offers the potential of using that network to examine various strategies obtained by selectively changing the inputs to observe the corresponding changes in the output. In this case, Run 11 was chosen as the Most Representative.
What do these numbers mean? Are they good, bad or indifferent? Empirically, we can offer the following experiences based on hundreds of neural networks. If the sensitivities (impact) are .1 or less, for all practical purposes they can be ignored. Inputs with a .1 to .2 sensitivity are relatively low but in some circumstances that still might characterize a potential key driver of the output. The maximum sensitivities in most situations usually lie between .2 and .4. Anything over .4 is relatively high. In this example, .53 raises a red flag. It is very high and points to a potentially important input. The sensitivity, or the impact it has on the output, however, is only half of the story.
The other half
The objective in this particular example was to determine the most effective actions that could be taken to transition the service call customers who were Somewhat Satisfied to Totally Satisfied. The neural network identifies the impact or change that occurs on Overall Satisfaction by changing any specific input. To determine the appropriate actions, however, the current level of satisfaction of each input must also be considered.
The table in Figure 12 shows the percentage of the customers who were Totally Satisfied with each of the five key inputs for the three basic groups: Totally Satisfied Overall, Somewhat Satisfied Overall, and Dissatisfied Overall. A combination of the data from the Somewhat Satisfied Overall group associated with the corresponding sensitivity (Run 11) will be used to clarify the appropriate actions.
 |
A presentation format called the Payoff Profile is used to graphically combine both aspects, plotting the level of satisfaction for each input and the impact that the input has on the output (Overall Satisfaction). Figure 13 illustrates this. The vertical axis measures the percentage of customers who are Totally Satisfied with each specific input. The horizontal axis measures the impact that each input has on the Overall Satisfaction.
 |
The maximum leverage occurs when there is a high impact (sensitivity) and a low satisfaction (the lower right-hand portion of the plot). The least leverage is when there is a relatively high satisfaction and a low impact (upper left-hand portion). The single input plotted as an example illustrates that 37 percent of the respondents were Totally Satisfied with that particular input and that its impact on Overall Satisfaction was relatively small at approximately 12 percent. This would not be a good candidate for action.
It is clear from Figure 14 that fixing the computer problem the first time is the most critical action that can be taken. The second possibility is assuring that the service person arrives at the customer's premises on time. These two actions would be the key strategy to convert the Somewhat Satisfied Overall group to Totally Satisfied.
 |
Normally Payoff Profiles for both the Totally Satisfied group and the Dissatisfied group are also developed and can sometimes impact the choice of the appropriate corrective actions. The Totally Satisfied group rarely has an input with an impact that is greater than .2 and typically all inputs have very high satisfaction ratings. For this reason, the Totally Satisfied Payoff Profile usually does not impact the decision for choosing the most effective actions. The Dissatisfied Overall group, on the other hand, almost always has a very low satisfaction rating with all of the inputs and often has a corresponding high impact for some of those inputs. The impact of the Dissatisfied on the final decision for selecting the appropriate actions will depend upon the percentage of customers in each group. In this example, there were very few Dissatisfied customers; consequently the improvement strategy is based solely on the Somewhat Satisfied Overall group.
The final subtlety
An initial step in the process of creating a neural network was to calculate a correlation matrix to determine if there were any strong relationships between the various inputs. In the example, there were several. If we create a network using inputs that are highly correlated this could lead to a very inaccurate result. Therefore, "proxy" inputs are typically selected to represent the correlated input groups. This process was described in detail in the previous installment of this article.
In the example, there were originally eight questions on the survey that served as inputs to the customer's decision process in determining Overall Satisfaction. Three were eliminated for the final derivation of the neural network because they were highly correlated with several of the five that were finally used. The three were:
- The ease of requesting service (Request)
- Effectiveness of the service representative in informing the user about the repair (Result)
- Communication from the service representative after the repair has been completed (Communication)
It is now necessary to go back to these correlated inputs to see if there are additional elements to consider in the final analysis. A correlation matrix should be developed again with all of the inputs (see the July/August issue), however only the data from the survey respondents who were Somewhat Satisfied Overall should be used in calculating it. In the example, there was only one highly correlated relationship to "First Time" and that was "Result." There were no highly correlated inputs to "Arrival."
Therefore the advice to be given, as a result of the analysis, is that the most critical action that can be taken is to assure that the repair of the computer was correct the first time. In addition, there should be an ongoing discussion during the service call to keep the customer up to date with the progress. A secondary but important element is to make sure that the service personnel arrive on-time.
The test of time
This technology is extremely powerful and it has withstood the test of time. It effectively accommodates the non-linearity and complexity of the human decision process. It has also been our experience that often the results that are obtained by using a neural network to analyze a survey are quite different than those developed by traditional methods. We have gained considerable respect for the value of neural network analysis: The outcomes that our clients have had by following the recommendations developed by this technique have been almost exactly as predicted.
The example used to explore the use of neural networks was based upon a customer satisfaction problem. We had a case study also based on customer satisfaction published in the October 1998 issue of Quirk's Marketing Research Review entitled "A Strong Connection." We have also used it for employee satisfaction, product design, medical analysis, characterizing ideal bank branch locations, defining buying factors, and many other areas.
Neural networks have become an accepted and very useful technology during the last decade. Their use is pervasive in many elements that impact our lives. They run elevators, fly airplanes, identify financial fraud, are used in medical analysis and in thousands of other applications. However, in our discussions over the years, it is apparent that there is very little active use of this technology in market research. It is our hope that this series of articles will stimulate interest and discussions about the value of using neural networks for survey analysis. There is an initial learning curve and a clear complexity that needs to be understood to effectively use this methodology and obviously there are areas that were glossed over in these articles for the sake of brevity. However, we would be glad to share our experiences with any interested individuals.
Author's note
There are two people who were very influential in convincing me to write this article. I would like to thank Chuck Kenney of Research Data Inc., who became a believer many years ago and tried to convince his clients of the value of neural networks. I am also indebted to Renee Rogers of Sulzer Orthopedics, who, in addition to being one of the first clients to use neural networks, had the patience and tenacity to sit through a long explanation of the minute details of the process and to encourage me to document the methodology for others.