Part I: An introduction
Editor's note: Robert Brass is president and co-founder of Development II Inc., a Woodbury, Conn., research firm.
This is the first of three articles aimed at describing a practical "how to" methodology for using neural networks as a technique for analyzing survey results. It is based upon eight years of experience in the development and use of this process. The reason for writing this article is to raise the awareness of the value of neural networks and their exceptional accuracy and hopefully to encourage others to add their ideas in furthering neural networks' evolution for use in market research. The approach of this serialized article is to present a mixture of theory, metaphors, and practical examples that will illuminate the subject in an interesting and comprehensive manner.
This first article will focus primarily on the fundamentals and background of neural networks, specifically as they are used as an analytical tool. The second article (appearing in the July/August issue) will leverage the example introduced in this first section and follow it through the development of multiple neural networks. The final article (October) will focus on the selection process to identify the "representative" neural network, how then to use it as an analytical tool and finally, how to present the results in an understandable and comprehensive fashion.
What is the problem to be solved?
The typical survey accumulates data to describe what people think. Frequently, however, the real value comes from understanding why people think the way they do. This allows answers to questions such as:
- What is the most effective way to improve customer or employee satisfaction?
- Why do customers buy a specific product?
- Why will a particular candidate appeal to a large group of voters?
The specific use of neural network analysis described in this article focuses on the "why" aspect of the analysis.
Costs and other elements of practicality usually limit the number of respondents to most surveys to less than 1,000 - more often less than 500. This means that any process for evaluating surveys should be structured to accommodate that limitation. This definitely influences the methodology for using neural networks, as will become obvious in the ensuing discussion. If, however, the total responses to a survey were in the thousands, some of the steps described could possibly be eliminated. This also will become obvious in the description of the analysis technique.
Why consider neural network analysis?
Human decision processes typically occur with incomplete information, are complex, nonlinear, and highly influenced by subtle circumstances. Each element involved in the decision tends to have a uniquely different relationship with the process and there is usually a high degree of correlation among many of the constituent elements that form a decision. Very seldom are they all independent of each other. These realities unfortunately do not bode well for the traditional methods of analysis.
Multiple linear regression for example, assumes linearity, and inputs that are independent. Nonlinear regression usually starts with the assumption that each variable has the same functional relationship to the output and does not accept input correlation graciously. Regression also requires considerable experience to master. Even then it is quite limited and typically requires interpretation of the results.
Neural network analysis simplifies or eliminates many of the shortcomings of regression. Where traditional statistical models require well-defined or at least partially defined domains to be effective, neural network models can handle highly unstructured data, similar to the mode of the human thought and decision processes.
Some may argue that neural networks are too abstract and not as reliable as regression, yet Kuan and White (1994) demonstrated that multivariate linear regression is a special case of a neural network model.1
In attempting to characterize priorities, another favorite technique is to ask the respondent to quantify importance. This, however, is fraught with issues. Consider the example of an evening at a restaurant. The respondent could be asked to rate the food, the company, the service, the atmosphere, the time to wait for a table, the selection from the menu, the price, etc. In addition he or she could be requested to estimate the importance of each in influencing their overall opinion of the evening. It could have been "excellent," "average," "fair," or "poor" or some other metric of measurement. It seems rational to assume that this is a very complex process. A mediocre meal with an enjoyable companion may be seen as an "exceptional" evening, while a great meal with rude service could be viewed as "poor." In fact if the dining experience was seen as being "excellent," the decision process is probably considerably different than if the evening was a disaster and considered "poor." The decision process is complex, certainly non-linear and very dependent upon the circumstances; consequently personal ratings of importance may be based upon different evaluation criteria.
Finally there is the problem of applying quantification (a number) to a literal description to allow a realistically relative rating to be evaluated. If "exceptional" is a 10, is "average" a 9 or an 8 or even a 5? The reality is that the substitution of a number for a literal can make a fundamental difference in ranking on a numeric scale. Since the choice of a scale is just a guess, this adds another dimension of plausibility in prioritizing elements by rating importance.
Neural networks offer another option. They are part of artificial intelligence technologies and operate as a simplified computerized model of the neural architecture of the human brain. Just as the human brain "learns" from repeated exposure to neural stimuli (or recognition of patterns - factual and behavioral), the neural network is also a pattern recognition system. Existing applications of the technology include models that have learned to speak, fly airplanes, detect fraud, identify galaxies, predict the outcome of horse races, predict future trends in commodity prices, and to diagnose illnesses.
In the application for analyzing surveys, Hornik et al. (1989) noted that the non-parametric nature of neural network models makes them particularly suited for social science data, where the assumptions of normality and linearity cannot be assured.2
The history of neural networks as a method for survey analysis
Let's be perfectly honest: Neural networks have a very poor reputation as a methodology for analyzing surveys. Historically, this impression is quite justified. Some of the problems stem from the difficulty in learning the process or how to interpret the results, but most of the negative reactions occurred as a result of incorrectly applying the technology. There is a basic reason for this inappropriate usage.
The most frequent use of neural networks is to develop a model. Used as a model, the goal is to predict an output given any set of inputs. When, however, it is used as an analytical tool, the objective is to find the effect that any single input has on the output(s). The problem arises since two neural networks developed from the same data and trained in the same way, with similar statistical assessments, can function almost identically as a model; however the impact that any single input has on the output can be significantly different. This is the rule, not the exception and this is also the fundamental reason that most attempts to use a neural network to analyze a survey have been unreliable.
As will become apparent in this and later parts of the article, circumventing this debilitating issue requires a change in the approach for creating neural networks. It also needs a different evaluation technique for identifying the optimum network to represent the decision process captured by surveys. In summary, employing a neural network as an analysis tool demands a totally different set of assumptions and processes than building a model.
Our experience with neural network analysis
In the late '80s, the emergence of a practical method for developing neural networks based on "back propagation" seemed to offer a promising methodology for addressing the shortcomings of the current methods of analyzing surveys. It was apparent that it could accommodate the non-linearity of the human decision process. As many attempted to use it, it became apparent that the results obtained were frequently illogical and clearly incorrect. After the initial enthusiasm it was hastily abandoned.
We began using neural networks to analyze surveys in 1994. The memories of the overstated potential of artificial intelligence in the '80s made our clients understandably skeptical. We tried various strategies including making up different names so we did not have to mention the "n" word. We also had some very interesting discussions with some very competent statisticians who were employed by our clients; their kindest reaction was a mild questioning of our sanity. Relief came from a surprising source: data mining. Since business tends to have love affairs with the latest theories, and neural networks were part of data mining, legitimacy arrived on a silver platter in about 1997.
To progress from the neural network basics to an effective analysis tool took several years and a lot of hard work that included several dead-ends. One event in particular stands out as symptomatic of the effort. To address a particularly difficult problem we rented a half a dozen 386's and let all of them, plus a few office computers, run over a three-day weekend to obtain the analysis we needed. We left the office with fingers crossed, hoping that there would not be a power failure; there wasn't and we obtained the results we needed. Fortunately, contemporary computers allow the same level of calculations to be completed on one machine in less than an hour, but for several years working with neural networks was more of a marathon than a sprint.
We can now attest from our experience that the correct use of a neural network as the basis of an analysis tool for surveys is extremely powerful and accurate. We have employed this technique since 1994 and have successfully used it for clients several hundred times. We have sufficient long-term relationships with many of those clients to be able to track the results of recommendations developed by neural network analysis and can say without qualification that the actual events occurred almost precisely as predicted. It is now our standard process for all of our survey analysis.
Neural networks 101
While the technical details of neural networks tend to be more than most want to know, a basic understanding is very important before attempting to use it as a survey analysis tool. The easiest way to gain a comfort level is to relate its learning strategy to a common occurrence that many of us have had or heard about. Perhaps you or your children learned multiplication tables with flashcards. These had one multiplication "fact" printed on each of 100 cards, but not the answer. Someone would show them to you one at a time. You had to initially guess the answer and if you were wrong, you would be told the correct result. You probably went through them many times before you could respond to every one correctly.
At first, you looked for the shortcuts. The zeroes were easy, so were the ones and the twos. You understood those patterns almost immediately. Probably the next numbers you learned were the fives or the nines. You learned the various tricks. The twos for example were the same as an addition of the number to itself. The nines were a little more difficult, but if you took the number that was to be multiplied by nine and subtracted one from it that was the first digit. The second digit was the difference between nine and first digit.
You generalized. It was certainly easier then memorizing and if the early results inevitably indicated that you had more to learn you would go back to the flashcards again and again until you had finally figured out all 100 facts.
 |
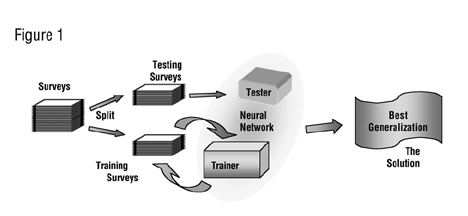
When used to analyze a survey, the neural network does the virtually same thing but with a slight twist. The survey results are randomly divided into two groups (Figure 1). One group is the "training" group while the other is the "testing" group. The input elements that could influence an outcome are presented to the neural network. Initially, it "guesses" the outcome or output (for example the overall impression of the dining experience). If it is wrong, it "nudges" its internal logic so the "guess" is closer to the right answer.
The normal training strategy is to stipulate the degree of error that is tolerable and not modify the network unless the actual error exceeds that limit, thus it will review this training group perhaps 20 times, nudging when necessary. Then, to evaluate the state of its learning, it takes a test. It reviews the testing group one survey at a time and keeps score of the correct answers and maintains the key statistical measurements of all of the answers. It continues to alternate between training and testing while keeping score of the results each cycle.
With continued training, the test scores usually rise for a while. Then it begins to memorize the training group. The result is that the trained neural network begins to make more errors on the testing group as memorization replaces the ability to generalize. The goal is to stop the training when the inherent patterns in the survey results have been maximally generalized and before the neural network shifts to a memorization mode.
 |
The computer program that forms the basis of the neural network is constructed from a number of simulated neurons, similar to the neuron in the human brain (Figure 2). Each of these "artificial neurons" is a processing unit that mathematically calculates the weighted sum of the inputs to create an activation level which is then passed through a transfer function to create an output. These artificial neurons are then combined into fully interconnected networks consisting of three classes of layers, the input, the output, and the hidden layer (Figure 3). During the training process, the strength of an input to a neuron (called the weighting) is nudged positively or negatively depending upon the error in the output. This cumulatively develops the logic of the network.
 |
Its intelligence is related to the number of artificial neurons and to the degree of interconnection. The number of neurons in the input layer is equal to the input elements and thus fixed. The output consists of the dependent variable(s) and is also fixed. There might be one output, which is normal for survey analysis, two outputs as illustrated in Figure 3, or even three or more. The major variability in the network, therefore, lies in the hidden layer(s). This can vary in both the number of neurons and the number of layers. In practical applications, however, two layers tend to be the maximum (Figure 4) and one typically suffices. Also, as a rule of thumb the number of neurons in these hidden layers is usually less than the number of input neurons when it is used for survey analysis.
 |
The important conclusion from this discussion is that there are several parameters that can be altered in combinatorial sets to develop different neural networks from the same data. The intent of creating a multiplicity of networks is to optimize the chance that the "most representative" one is included among those that were trained. The identification of this specific network among others is the critical step in analyzing a survey. It should be noted that the representative network is rarely the "best" network in terms of statistical accuracy. The variables that determine the development and variability of networks are:
1. The architecture of the neural network (the number of hidden layers and the number of neurons in each of the layers).
2. The training strategy (the degree of error that is permissible and the amount of adjustment to be made if the error exceeds the limit).
3. The order of the training group (alternative sequences of the training deck can create significantly different networks).
4. The division of the training and testing surveys (the division of the surveys into two groups).
This last variable, the split of the training and testing decks, is extremely critical. Each time the survey results are divided into those two groups, a bias is most likely interjected into the resulting neural network. This is simply due to the natural statistics of small numbers. Therefore, a relatively large number of separate segmentations and resulting networks are required to increase the likelihood that a representative neural network can be created and then identified. The process for selecting the optimum network will be described in the next installment of this article.
An example
To make the acquisition of knowledge less painful, we will use an example to illuminate each step of the way. Consider the following:
A growing company provides repair service for Internet servers and would like to insure that they maintain a high level of customer satisfaction. A customer satisfaction survey has been designed to be given to each customer after a service call. The goal is to quantify and prioritize the impact that eight specific elements of that service call have on overall satisfaction. The eight elements are:
1. The ease for the user to initiate a request for service.
2. The time for the service representative to call and set up an appointment.
3. The time it takes for the service representative to arrive.
4. The conduct of the service representative during the service call.
5. The service representative's effectiveness in informing the user about the repair.
6. Communication from the service representative after the repair has been completed.
7. The ability to fix the problem on the first try.
8. Responsiveness of the service representative to requests during the service call.
When the survey was tabulated there were 920 viable results, grouped into three segments: 86 percent were Totally Satisfied Overall, 10 percent were Somewhat Satisfied Overall and 4 percent were Dissatisfied Overall. Since the goal is to quantify the sensitivity of the eight elements on their effect on Overall Satisfaction, the first rule of thumb is: You should approximately balance the survey segments to optimize the detection of sensitivities.
It is tempting to use all 920 respondents, however the Totally Satisfied segment would tend to drown out the Somewhat Satisfied segment. The Dissatisfied segment, at only 4 percent, will be overwhelmed by the other two segments and thus any results for this particular group must be viewed with caution.
From a corporate strategy viewpoint, the major opportunity is to encourage the Somewhat Satisfied Customers to become Totally Satisfied. As a result, a random group of 104 Totally Satisfied survey respondents was chosen from the 920 originals and combined with the 92 Somewhat Satisfied and the four Dissatisfied. This total of 200 was selected to observe the second empirically-derived rule of thumb: The minimum rational number of survey respondents for a neural network analysis is 200.
The reasons for this minimum are somewhat involved but relate to the number of interconnections internally between "neurons" in the neural network. This brings up another limitation that is expressed in the third rule of thumb: The maximum number of inputs for a neural network survey analysis is one-half the square root of the number of survey respondents used.
It becomes immediately apparent, given these rules of thumb, that there is a problem with the number of respondents that can be used (200) and the number of elements that need to be evaluated (eight). One half of the square root of 200 (number of surveys to be used in the analysis) rounds to seven, but there are eight elements to be evaluated. A gap is quite typical in that the number of inputs is almost always much greater than the allowable number. The method of working around this issue is the first critical step in using neural networks for evaluating surveys. This will be discussed in the next article.
These "rules of thumb" were developed over several years by evaluating thousands of different alternative cases using neural network for analysis purposes. They are based upon establishing criteria that will assure a robust and relatively accurate result. There are situations where these limitations have been conservative, but on balance these are appropriate.
Valuable method
Neural networks, if used judiciously, can be a very valuable method for analyzing surveys. It is a practical way to accommodate the inherent nonlinear process we all use for decision-making. In addition, the correlation that often exists among many survey questions which impact a decision is not an obstacle for developing a viable network. The current lack of use most likely stems from a basic misunderstanding or problems that have occurred with it in the past.
The second article will develop the details of the process for the preparation of the data for analysis, the building of multiple neural networks, and the method of selecting the most "representative" network for analysis.
References
1 Kuhan, C. and White, H. "Artificial neural networks: an econometric perspective." Econometric Reviews, 13 (1): 1-91 (1994).
2 Hornik, K. Stinchombe, M., and White, H. "Multilayer feed forward networks are universal approximators." Neural Networks, 2:359-66 (1989).