Part II: Building the networks
Editor's note: Robert Brass is president and co-founder of Development II Inc., a Woodbury, Conn., research firm.
Last month, at the conclusion of the first of this series of three articles, we had just introduced an example that would act as your guide through the development of the neural network analysis process for survey results. To maintain consistency, the numbering of the figures and rules of thumb in this segment will continue where we left off.
For those of you who cannot conveniently locate the first article of the series, or who are just now deciding that this one might be interesting, we will restate the example. It proposed a business that sent service technicians to fix faulty Internet servers. Following the completion of the service, a survey was sent to the customer to assess their satisfaction level with the repair and the subsequent outcome. There were eight elements that were evaluated (input questions) plus an overall question (output question) to gauge the totality of the process. They consisted of:
1. The ease for the user to initiate a request for service (initiate).
2. The time for the service representative to call and set up an appointment (appointment).
3. The time it takes for the service representative to arrive (arrival).
4. The conduct of the service representative during the service call (conduct).
5. The service representative's effectiveness in informing the user about the repair (result).
6. Communication from the service representative after the repair has been completed (communication).
7. The ability to fix the problem on the first try (first try).
8. Responsiveness of the service representative to requests during the service call (requests).
9. Their overall satisfaction with the service call that repaired the server (overall).
As discussed in the last article, 200 individual surveys were finally chosen to be used for the analysis. This, as described previously, limits the total number of input questions that can be evaluated (the third rule of thumb) to seven. The next step, then, is to identify the questions that will be chosen as the inputs to develop the neural network and those which will be eliminated.
Correlation, the Achilles heel of survey analysis
The phrase "a rising tide lifts all boats," in an abstract way applies to customer satisfaction, employee satisfaction, product selection, and many other surveys. It relates to the phenomenon that there is a normal correlation that exists between the majority of the respondent's answers in a typical survey. For example, in a customer satisfaction survey, a person who is Totally Satisfied Overall is probably quite satisfied with most of the other surveyed elements that influenced that decision, while a dissatisfied individual is likely to have several associated areas of dissatisfaction.
Correlations in the answers to surveys consist of two types, incidental correlations and topical correlations. Topical correlation occurs when there is a logical link among question topics. In the example, there are several areas of query that exhibit this characteristic. As an illustration, consider:
1. The conduct of the service representative during the service call.
2. Responsiveness of the service representative to requests during the service call.
The correlation between these two queries is topical since the major interaction that a customer has with a service representative is usually a request or a question and the evaluation of their conduct would be how well they responded. This suggests that upon inspection of a large number of respondents' answers that a high correlation can be expected to exist between the answers to these two question topics. On the other hand "the time for the service representative to call and set up an appointment" is not significantly related to the prior two question areas and thus it would not be expected to exhibit a topical correlation with either of them. The level of satisfaction indicated for this question, however, will still probably have a correlation with those previous two, but to a smaller degree. This would be the incidental correlation that occurs simply because of a relative consistency in the answers to most questions.
Incidental correlation is background noise that we do have to live with. Topical correlation on the other hand should be minimized. The reason to eliminate as much topical correlation as possible can be understood by the following "thought experiment."
Hypothetically, when building a model to analyze customer satisfaction (for the example used in this article) instead of using one input for each question, suppose you create 10 separate inputs from the answers to first question (the conduct of the service representative). The remaining seven input questions, on the other hand, would be given only one input each. Clearly then this "conduct question" would dominate the logic of the model. Thus, any attempt to understand the objective impact of the conduct question would be highly distorted. It would also dilute the impact of the other questions on overall customer satisfaction. A similar dilutive situation results when there exist significant topical correlations among questions if they are all used as inputs to a neural network.
The goal, therefore, is to minimize topical correlations. Minimization is accomplished by elimination! The challenge is to determine what should be eliminated and what should be saved.
The incidental correlations, on the other hand, will appear in almost every survey, thus there is a normal level that can usually be anticipated. This leads to the fourth rule of thumb:
Correlations below .4 are acceptable (this is typically the upper range of incidental correlation).
Correlations between .4 and .5 are marginal and should usually be eliminated.
Correlations between .5 and .6 are high and should be eliminated if at all possible.
Correlations above .6 definitely should be eliminated.
Correlations above .7 are highly indicative of questions that deal with virtually the same subject (from the respondent's point of view) and must not be used in developing neural network.
It should be emphasized that this rule of thumb applies to a four- or five-level scale and only to inputs, not the potential outputs of a neural network. A higher or lower number of levels will certainly result in different acceptable/elimination criteria.
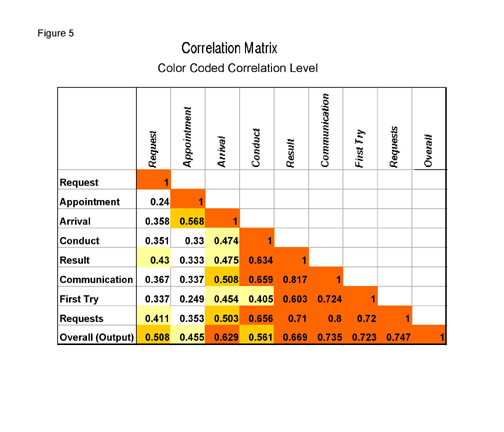
A simple process for identifying correlation among question answers is to use the correlation function in Excel. This is available in the Data Analysis function group listed under Tools. The output is illustrated in Figure 5, which is the result of calculating the correlations for the example.
 |
There are three color overlays to correspond with each of the top ranges of correlation, which visually aid in identifying those groups. This color coding, or one of your choice, is easily obtained by using the Conditional Formatting capability in Excel.
What to keep and what to eliminate
There is nothing automatic about deciding which questions to eliminate as inputs to the neural network. This selection process requires a reasonable understanding of the subject matter and some trial and error. It is important to note, however, that elimination from consideration as an input to the neural network does not mean that those questions are not included in the ultimate analysis.
The goal is to leave questions that include at least one (often more) which is highly correlated to those which are not used and to have a logical understanding of its relationship to the discarded questions. To accomplish this selection, normally we look for inputs that have the highest correlation with other inputs as a first guess for elimination. In this example, Result, Request, and Communication fit that bill. The next step is to determine if among the remaining, there exists a question that can be a proxy for the removed items. A high correlation is the clue for identifying it. In this case, it is Conduct. A further examination of that correlated group suggests that the common denominator is information about the Result of the service call.
The correlation that inputs have with the output, as seen in Figure 5, can also be used as additional information to aid in the selection of the final question set. Those that have a high level of correlation with the output should be given precedence where possible.
The final reduction is illustrated in Figure 6 with shading covering those questions that will not be used as inputs to the neural network. There is one high value of correlation that could not be eliminated. That is the relationship between Arrival and Appointment. This does happen occasionally and fortunately is not fatal.
 |
A reasonable question to ask is: Does this process always work? The answer is that it rarely doesn't. This does not mean that the first guess for selecting the inputs will always be the best. Very occasionally, we will have to redo the entire analysis. The indication that it should be considered is when the proxy question turns out to have the highest impact on the output by a significant margin over the next input. The approach in this case is to initially eliminate those inputs that were shown to have little effect on the output and then, to create the correlation matrix again and reselect a new set of inputs for the neural network.
Segmenting the survey respondents into logical groups
When using a neural network for identifying input sensitivities the non-linearity of the result must be considered. This means that, an "average" sensitivity for each input element over all respondents is probably inappropriate. Different groups of respondents can have very different decision processes, therefore it makes sense to assemble them into logical segments and derive average sensitivities separately for each of those segments. The details of this process will be explained in the third segment of this article.
There is no standard methodology for determining the optimum segmentation of the respondents. The choice will depend upon the analysts' experience with the specific fields addressed by the survey. There is, however, a practical rule of thumb for the number of groups when working with a neural network in most survey situations. This is the fifth rule of thumb:
Usually, the optimum number of groups that can be separately analyzed will be two to five.
Although this number may seem small, the total number of respondents in each segment is what creates the limitation. Ideally there would be about 80-100 respondents, as a minimum, in each group. With 200 survey respondents, for example, two groups is the reasonable maximum.
In the case of this customer satisfaction example, the segments would be:
1. Totally Satisfied Customer
2. Somewhat Satisfied Customers
3. Dissatisfied Customers (a combination of the Somewhat and Totally Dissatisfied Customers)
The final data set selected for this analysis consists of 104 Totally Satisfied respondents, 92 Somewhat Satisfied, and four Dissatisfied. This selection was derived from the total survey responses to balance the first two categories and to have a small but representative group of the Dissatisfied. The inclusion of the Dissatisfied group would normally be questionable, however it is part of this example for illustrative purposes. It is used only in creating the neural network, not in the analysis.
Scaling the inputs and outputs
Although the respondents' choices for selecting a customer satisfaction level are often given as literals, such as in this example, the neural network requires numerical values. The selection of a specific number for each level in the satisfaction scale, therefore, is important. The first step is to identify the key segments of the data. Since the intent in this example is to select the optimum actions to create the maximum number of Totally Satisfied customers, it and the Somewhat Satisfied segments are the most critical. The Dissatisfied group is small to begin with and will probably respond to any corrective actions applied to the Somewhat Satisfied group.
The goal, therefore, is to assign numerical values to maximize the quantitative distance between the key groups, to allow a greater range of discrimination. This results in a somewhat non-intuitive solution, as usually higher numbers are associated with higher levels of satisfaction. Our approach is the reverse, as indicated in the following selection.
Totally Satisfied = 1
Somewhat Satisfied = 3
No Opinion = 4
Somewhat Dissatisfied =5
Totally Dissatisfied = 7
Since the neural network is structured to deal with ratios, the distance (ratio) between Totally Satisfied and Somewhat Satisfied is 3 (3/1) while the distance between Somewhat Dissatisfied and Totally Dissatisfied is 1.4 (7/5). The "No Opinion" answer must be represented as it is a valid answer and therefore it is squeezed between Somewhat Satisfied and Somewhat Dissatisfied in an attempt to minimize its impact. Since it is necessary that every input of every respondent used to train or test a neural network have a numerical value, No Opinion could also be used for a question that the respondent chose not to answer.
Using the substitution of the values 1,3,4,5,7 for the literals allows us to calculate an average for each of the selected inputs for the three key segments. This is illustrated in Figure 7.
 |
The neural network (finally)
The preparation and selection of the inputs constitutes the majority of the work, as clearly indicated in this article. The derivation of neural networks from these inputs, on the other hand, is somewhat automatic.
We have chosen BrainMaker, from California Scientific Software, as our "engine." The advantage that BrainMaker offers for our process is that it has the ability to control network configurations and training strategies. Most important, however, is that it also has an option called GTO (genetic training option) that allows us to predefine a range of alternatives to be iteratively implemented during a series of training sessions. Without this capability, as will become apparent, the development of the thousands of neural networks that are necessary for a proper analysis would be overwhelming.
The fundamental calculation derived from a neural network analysis is a value for the sensitivity of the output (Overall Satisfaction in the example) to each of the separate inputs. This derivation is required for each of the key segments. As could be expected, the sensitivities of each input will usually vary considerably from segment to segment.
While different neural network software programs have a number of strategies for calculating sensitivities, BrainMaker varies each input by 10 percent of its range (maximum value - minimum value) and calculates the fractional change in the associated output. This calculation does not, however, directly provide the sensitivity in a format that we can use.
What is sensitivity? The goal is to determine a dimensionless number that has a consistent calculation for both the input and the output. While there are several options, we use the ratio of:
Sensitivity (or Impact) = Percent Change of the Output/Percent Change of the Input Variable
For each segment there will exist an average value for each input. Since the individual range of these inputs is also known, dividing (in the specific segment) 10 percent of that range by the average input value will calculate the "Percent Change of the Input Variable." In a similar fashion, BrainMaker has a function that will display the change in the output corresponding to each standard input variation (10% of the range), one at a time. This value divided by the average value of the output for each segment defines the "Percent Change of the Output."
The fundamental strategy for developing a neural network for survey analysis
There is a major difference when developing a neural network to analyze a survey, as opposed to deriving a model. When building a model you seek to identify the statistically best network. When used for analysis, the objective will be different, in that your goal is to find the most "representative network." This is usually not the "best" network. The reason for seeking what we refer to as a representative network stems from the limited number of survey respondents that are usually available.
Most suggestions for building neural networks recommend that 10 percent of the data be used to test a network that was trained with the other 90 percent. Unfortunately, this portion of the respondents' answers for testing is not sufficient for a small survey sample, therefore as the sixth rule of thumb we recommend that:
The minimum number of respondents used for testing is 80.
Testing data should consist of a minimum of 40 percent of all of the respondents.
The logic behind this rule of thumb is that the statistics for defining the characteristics of a neural network are derived from the "testing data," thus it should be a "statistically robust" group.
This rule of thumb was derived empirically from hundreds of frustrating experiments. The early conclusions were disheartening, as the recommended 10 percent testing sample most often gave very poor and even incorrect results. It became apparent quite quickly that the size of the testing group had to increase. As this testing sample increases, however, the training sample decreases and the major source of the statistical error begins to shift to the training group.
In solving one problem, as in life, you typically create another, and this was no exception. Since often a network is being built with as few as 200 survey respondents, by providing a viable number for testing you also introduce some interesting statistical biases in training, or vice versa. The rule of thumb then arose as a compromise but unfortunately with a sacrifice in statistical accuracy.
The strategy that was identified to overcome that issue was to initially create a very large number of separate neural networks. This is accomplished by a re-randomization of the survey data; then training, testing and creating additional networks. What was anticipated to emerge from the aggregate of all the networks, assuming the number is sufficient, will be a pattern pointing to a "representative network."
Creating the iterations of the data for training the neural network
To create the multiple networks which are needed to optimize the probability of finding a common central pattern, it is necessary to develop a number of fundamentally different networks from the same data.
The discussion to explain this process will reference the capabilities of BrainMaker's GTO. It will be general enough, however, to be applicable to other neural network software packages. The major options, other than a re-randomization of the respondent data and the subsequent splitting of it into training and testing sets, are the training strategy and the network architecture.
Training is enabled by a property called tolerance. In BrainMaker, tolerance is defined as a specified percentage of the range of the output. In training, a correction is only made to the network if the output for any set of inputs exceeds that tolerance. This tolerance can be set to a constant or a dynamic value that decreases in a predetermined pattern as the network increasingly learns from the training facts.
The network architectural variability comes from the number of layers of hidden neurons in combination with the number of neurons in each of those hidden layers. From a practical point of view, and also a limitation of BrainMaker, two layers of hidden neurons are the maximum that can be used.
Stipulating the iterations for developing multiple networks
As implied in the previous section, the crux of the process for identifying the representative network lies in the ability to generate a sufficient number of different networks from the same data to insure that a rational representative pattern will emerge in the aggregate results. The following is a description of the methodology that BrainMaker allows us to use.
Labeling the criteria as rules of thumb is a stretch, so instead, consider these alternatives as "what works well for us."
1. In training, reviewing all survey respondents in sequence 210 times is usually sufficient. This is called a training cycle.
2. Test after reviewing the complete sequence of survey respondents every 30 times (seven times per training cycle).
3. For the fixed training strategy, a training tolerance of .1 (10 percent) works well.
4. For the variable training strategy, a beginning training tolerance of .2 (20 percent) decreasing in the sequence .16 (16 percent), .13 (13 percent), and .1 (10 percent) is effective. Each successive step is taken when the network is trained such that 90 percent of the training facts are within the current tolerance.
5. For the first hidden layer, start with the number of neurons equal to 25 percent of the inputs and continue by adding two neurons in each new training cycle until it is equal to 120 percent of the inputs.
6. Add a second hidden layer using the same strategy as the first hidden layer.
7. Iterate until you have used all possible permutations of the previous alternatives (1-6).
8. If the total number of training cycles exceeds 100 consider increasing the two-neuron increment to three or four.
With a total number of cycles that could equal 100, there might then be 700 potential tested networks to choose from. This number, however, is only for one split of the survey respondents between testing and training. In fact the respondent base should be reshuffled at least four or five times, as a minimum, and retrained each time using the parameters defined above. This generates a maximum of 2,800-3,500 tested networks. Although the development of all these networks sounds ponderous, it really isn't. The entire process including selecting the appropriate networks (exclusive of computer time and data preparation) takes slightly over an hour.
What is the result of all these calculations?
The selection methodology is a two-step process. The first is a preliminary reduction. From each re-randomizing of the surveys and subsequent training of multiple networks (about 700 networks), three are chosen that exhibit "optimum statistics" (to be discussed in the third article).
For explanation, (using the example) we will assume four re-randomizing sequences. The results, after normalization, are illustrated in Figure 8. Only the table for the Somewhat Satisfied group is shown here. Similar tabular results exist for the Totally Satisfied and Dissatisfied. There are 12 selected "best networks" shown. Each row (of the 12) defines the impact or sensitivity for each input (the satisfaction element) on the output (Overall Satisfaction). The ratio is given as a percentage. By examination of Figure 8 it is important to note the extreme differences in sensitivities of the inputs in some of the 12 selected networks!
 |
Like a good soap opera, we leave this second article with a cliffhanger. Observing the dramatic differences that can occur in the outputs of neural networks developed from the same data raises two "sticky" questions.
1. If you presently use neural networks for analyzing surveys without consideration of the issues raised so far in this article, "Are you feeling lucky?"
2. Given this apparent variety of results, how do you identify the correct representative network?
Although the selection process was originally slated for discussion in this section, it is postponed until the third article. Tune in for the explanation in the October 2002 issue.