Editor’s note: Susie Sangren is president of Clearview Data Strategy, an Ithaca, N.Y., consulting firm.
My January 1999 Data Use article focused on the mechanics of calculating the sample size for a simple random sample survey at a prescribed level of precision, in an ideal state. But the world is not ideal: We rarely have the luxury of doing a true random (equal opportunity) sample survey, and we have to accommodate many conflicting demands. In this article, I address those external demands and their effects on your sample, and offer solutions. I then propose stratified random sampling as an alternative to help you achieve the same level of accuracy as computed on a simple random sample with a reduced sample size.
Compromise between practical constraints and technical elegance
When was the last time you actually knew the entire population before you took the survey, which is a pre-requisite for any random sampling to ensure that everyone in the population has an equal chance of being selected into your sample? In some cases, we might use a convenience sample, a judgement sample, or a quota sample (all of them non-probability sampling) without realizing that it isn’t a random sample.
- A convenience sample is convenient to take for the surveyor. For example, a doctor may select the patients treated at his hospital for a clinical study.
- A judgement sample is one taken by an overeager expert believing that, with his intimate knowledge of the individuals in the sample, the sample must represent characteristics of the population. For example, the leader of a school board may choose four of his allies on the board to represent the opinion of all members.
- A quota sample is one in which the population is subdivided into several sub-populations or, strata; within each stratum the surveyor is free to select individuals in any manner he wishes, usually by way of a convenience sample or a judgement sample, until he reaches the specified number of individuals.
All of these samples share one thing in common: there is no knowledge of their representativeness (of any population) and their reliability because they are not random samples. Does this mean that we should abandon our efforts in calculating probability-based sample size for them, drawing statistical conclusion at the required level of precision and confidence intervals? Absolutely not. If we are doing something wrong, we might as well do it in the most effective way!
Statistics, though not applied optimally, can in so many ways dramatically improve operating efficiencies, cut costs and improve estimation for a survey. We should, however, be mindful that what we calculate are: approximately unbiased sample estimates and their precision, approximately valid confidence intervals; and sample sizes that are based on quantifiable statistics rather than some arbitrary industry standard.
Close substitutes for simple random sampling
- Systematic sampling is a probability-based sample design often used when a listing is available and can be ordered. You would select every kth element in the population, after a random start somewhere within the first k elements. For example, suppose you have a list of 5,000 households in a city, and you want to sample 100 households. Your interval, k, would be 50 (=5,000/100), or every 50th household. You would then select a random number between one and 50, say 13, and survey the houses numbered 13, 63 (=13+50), 113 (=63+50), 163 (=113+50), and so forth.
Systematic sampling is used more often in practice than simple random sampling because it is much easier and cheaper to do. It has two advantages:
1) You do not jump back and forth all over the list wherever your random number leads you, and you do not have to worry about duplication of a sample.
2) You can select a sample without a complete list of all households.
One major disadvantage with systematic sampling is “periodicity,” where you may encounter cyclical patterns. For example, a sample of every, say, 50th business from a list in New York City turns out to be located on or near Fifth Avenue. When this happens, you must reorder the list and redo the sampling.
- Random-digit dialing has become an important probability sampling procedure with the rising popularity of telephone interviewing. In its purest form, this procedure calls for randomizing all seven digits of a telephone number. However, this is too costly and inefficient. What is more common in practice is that numbers are selected from a telephone directory by first using a systematic sampling procedure, and then the last one or two digits of the numbers are replaced with random numbers. This procedure gives a much higher percentage of usable telephone numbers, and also has the flavor of a true probability sample.
Myth and reality about sample size
The general public seems to believe that larger samples are necessarily better than smaller ones. It simply sounds more credible to say: “Based on a study of 3,000 people” than to say: “Based on a study of 250.” This is partially true: What if only 8 percent of the 3,000 people responded, resulting in only 250 completes, whereas 100 percent of the 250 responded? You may only need 250 responses to attain the precision level for your estimate at a preset level of, say, within ±1 percent of error at the 95 percent confidence level. Remember that the sample size you need for computing precision is that of the survey “completes,” not the survey “mail out.” Once you take non-responses into consideration, a very small, well-executed sample may yield an estimate as accurate as that from a huge, sloppy sample.
I should also point out that the statistical precision requirement is only one of many considerations a researcher must face in choosing the sample size, and there is no one correct answer. Whatever his choice may be, the researcher should fully understand the consequence of the precision gain or loss due to his choice. Practical constraints, other than the precision requirement, affecting sample size decisions are:
- Time pressure. Often research results are needed “yesterday.”
- Cost constraint. A limited amount of money is available for the study.
- Study objective. What is the purpose of the study? A decision that does not need great precision can make do with a very small sample size. A company may be happy to measure interest in its new product within 15 to 20 percent of precision. A political pollster can be off by less than 1 percent and fail to predict the election result.
- Data analysis procedures. Data analysis procedures have an impact on the sample-size decision. The sample-size and precision formulae I have proposed so far are premised upon you doing a basic, one-variable analysis of frequencies. When you start doing crosstabulations examining the relationship of two variables at a time, you may run into situations where some cell sizes are so small that the precision of estimates within cells becomes suspicious. A study doing only one-variable analysis may only require 200 completed responses, whereas a similar study doing two-variable analysis may require over 1,000 responses.
Stratified random sample survey
If the population is first grouped (or stratified) according to some criterion, then a simple random sample is selected for every stratum. This type of survey design is a stratified random sample.
Quota sampling, undoubtedly the most popular form of sampling used in the research industry, closely resembles stratified random sampling, and should follow formulae developed for the stratified sample to approximate its sample size and precision. If you use the simple random sample calculations for a quota sample, you would overstate the error of your estimate and the sample-size requirement.
If intelligently used, stratification nearly always results in a smaller sampling error than is given by a comparable-size simple random sample (That’s why stratified sampling is statistically “more efficient.”) It is not always true though -- the key is in the careful selection of the stratification criterion. In constructing strata, you must always ask yourself: “Wat factor contributes most meaningfully to all the outcome variables I want to measure?”
As an example, suppose that you are asked to study personal income in some target population. The most important contributing factor to the differences in income may be education. Better-educated individuals earn more than less-educated ones. If you distinguish four levels of education (eight years or less in school, 12 years, 16 years, 17 or more years), you would have four different strata. In the “17 or more years” stratum, you may find most of the high-income earners. In the “eight years or less” stratum, you may find most of the low-income persons. The within-strata variability is much smaller than that across strata. Because you only need the within-strata variability to calculate the overall sampling error for a stratified sample, the advantages of a stratified design over simple random design become clear:
- For the same level of precision, you would need a smaller sample size in total, thus a lower cost.
- For the same total sample size, you would gain a greater precision for your estimate.
Conversely, if your stratification variable was so poorly chosen that the sample measurements are all over the place within a stratum, you lose all the advantages inherent in a stratified random sample. (You might as well do a simple random sample instead.)
There are two popular ways of assigning the sample size to the different strata, once the total sample size is determined: equal allocation - taking the same sample size from each stratum; proportional allocation - taking the sample size from each stratum in proportion to the stratum population size. Other methods exist to achieve even smaller sampling errors and reliable estimates. But they are complex and beyond the scope of this article. In general, the larger the stratum, the larger the sample size should be; the greater variability within a stratum, the larger the sample size should be.
An example
 |
Let’s suppose a business has the following employee profile:
- 62 percent are skilled or unskilled males;
- 31percent are clerical females; and
- 7 percent are supervisors.
From a total sample of 400 employees (n=400), the firm wishes to estimate the “overall” proportion of employees who use certain on-site fitness facilities. Rough guesses are that the facilities are used by 40 to 50 percent of the males, 20 to 30 percent of the females, and 5 to 10 percent of the supervisors.
A) How would you allocate the sample among the three groups?
B) If the true proportions of users are 48 percent (males), 21 percent (females), and 4 percent (supervisors), respectively, what would be the sampling error of the “overall” estimated proportion (Pstratum) with stratification?
C) What would be the sampling error from a random sample (Psimple) without stratification with the same sample size of 400?
A) Using the proportional allocation, we would assign the three stratum sample sizes as:
nstratum 1 = 400 x 62% = 248 to the male stratum
nstratum 2 = 400 x 31% = 124 to the female stratum
nstratum 3 = 400 x 7% = 28 to the supervisor stratum
B) If I guess Pstratum 1= 45 percent, Pstratum 2 = 25 percent, and Pstratum 3= 7.5 percent, then my overall proportion estimate is:
Pstratum = (45% x 62%) + (25% x 31%) + (7.5% x 7%) = 36.2% (which is a weighted average of the within-strata proportions)
And, my sampling error for the overall proportion estimate is calculated as:
Sampling error (Pstratum) = square root of {∑ WI2 [P stratum I (1- P stratum I) / n stratum I ]}
= square root of [(0.62 x 0.62 x 0.45 x 0.55) / 248) +
(0.31 x 0.31 x 0.25 x 0.75) / 124) +
(0.07 x 0.07 x 0.075 x 0.925) / 28 ]
= 0.02326 = 2.33%
where WI is the weighting factor for a stratum, i.e., the size of the population within a stratum relative to the total population.
The 95-percent confidence interval (= two standard deviations) for a total sample size of 400 is:
36.2% ± [2 x (2.33%)], or 36.2% ± 4.66%, or [31.54%, 40.86%]
Note: The true estimate is 36.6% = (48% x 62%) + (21% x 31%) + (4% x 7%)
C) With a simple random sample, my overall proportion estimate, Psimple, is the same as that from a stratified sample, 36.2 percent. However, the sampling error for this estimate is larger:
Sampling error (Psimple) = square root of { [ P simple (1- P simple) ] / n }
= square root of { [ (36.2% x (1-36.2%) ] / 400 }
= 0.02403 = 2.4%
The 95 percent confidence interval for a total sample size of 400 is:
36.2% ± [2 x (2.4%)], or 36.2% ± 4.8%, or [31.4%, 41%]
In this example, the improvement of sampling error from a simple random sample to a stratified random sample may not seem dramatic, from ±4.8 percent to ±4.66 percent. However, this difference amounts to a reduction of 25 interviews. (To achieve the same level of precision with a simple random sample, we would need 425 samples, an increase of 6.25 percent!)
n simple = square of {square root of [ P simple (1-P simple) ] / (E / Std. deviations) }
= square of {square root of [36.2% x (1-36.2%)] / (4.66% / 2) } = 425
where E = my desired level of precision, Std. deviation = expression equivalent to 95% confidence level
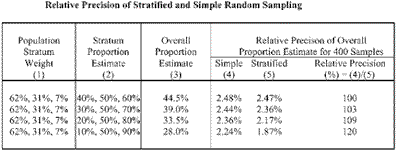
Finally, for a fixed total sample size, the gain in precision from stratified random over simple random sampling is the largest if the stratum proportion estimates vary greatly from stratum to stratum (i.e., great across-strata variability). I conclude with a table comparing the relative precision of stratified and simple random sampling for the above employee survey example with three strata and 400 samples, at various combinations of stratum proportion estimates:
Four cases are presented in the table, the first having Pstratum 1 = 40 percent, Pstratum 2= 50 percent, and Pstratum 3= 60 percent, and the last having Pstratum 1= 10 percent, Pstratum 2= 50 percent, and Pstratum 3= 90 percent. Columns 4 and 5 give the standard errors of the overall estimated proportion. The last column gives the relative precision of stratified to simple random sampling. The gain in precision is large only in the last two cases.