Editor's note: Steven Gittelman is president of Mktg, Inc., East Islip, N.Y. Adam Portner is senior vice president, client development at Research Now, San Francisco.
In the November issue, we laid the groundwork for our investigation into the degree to which a social network population sourced from Peanut Labs respondents could be blended with an established panel, Research Now’s American Valued Opinions Panel (VOP), while maintaining the original panel sample characteristics.
The behavioral differences between the VOP and Peanut Labs samples are significant. As a result, we suggest these sources are not directly substitutable for one another. When consistency of data is critical (wave studies, pre/post, tracking studies), uncontrolled introduction of Peanut Labs respondents into a Valued Opinions Panel sample could be problematic. Such a mixture may create considerable change in the characteristics of the original source.
The practical question of blending, therefore, becomes one not of finding those source respondents who will exactly replicate the panel respondents but of finding the correct amount of respondents who can be added without bringing about significantly different survey results.
While such a blending model could be developed for the sample as a whole, deviations between sources would likely exist within demographic cells. As such, a demographics-based blending is called for. A demographic matrix (by age and gender) was used. The question was, for each cell in the matrix, what fraction of the source could be added to the host sample without materially altering the resulting characteristics?
Two measurement issues
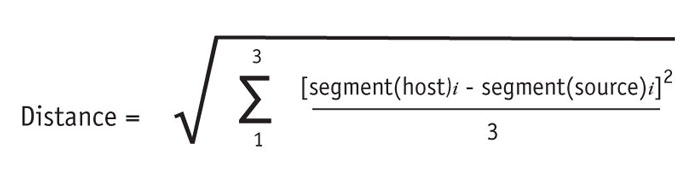
There are two measurement issues. First is how to measure differences between the two panels and second is determining the largest acceptable difference. Since this is a simple (linear) mixture, the acceptable maximum ratio would be equal to the largest acceptable difference divided by the measured difference between the data sources to be blended. The measured difference is taken as the root mean squared difference. That is, the square root of the average of the squared differences of the segments. For the buyer behavior segment, which has three subsegments, this becomes:
The media usage segment has four subsegments and that increases the number of items in the average. Note that these measures are computed for each of the segmentation schemes.
The acceptable distance is related to the expected error around the distribution of segments. This is taken as a root mean squared standard error. The standard error around each segment is given by the binomial formula:
Pi is the fraction of the sample in Segmenti of the host and N is the number of respondents in the targeted sample. Note that the number of respondents in the targeted sample is not necessarily the size of the sample used in the measurement. It represents the size of studies for which the test is being run. The total measure of error is the root mean square of these standard errors:
Finally the acceptable level is taken as some proportion, b, of the total standard error. We can look at this as a Type I error, that is, we seek the minimum acceptable likelihood that the two samples are the same. This is referred to as the a term. In typical statistical comparisons, an a term of 5 percent is generally implied, meaning the chances are less than 5 percent that the two samples are the same. This is a conservative threshold, chosen by scientists to minimize the chances that a given treatment is falsely said to have an effect. However, our intention is the opposite. We wish to establish at what levels our host and blended sample are not statistically different, and thus, a higher a is more conservative and appropriate. As such, we set our threshold at one standard error as the acceptable range which is equal to approximately a = 32 percent, rather than the usual two standard errors. This gives us two adjustable parameters in selecting a policy, the targeted sample size and the minimum acceptable likelihood.
Therefore the acceptable level is:
Acceptable Level = b X
Total Standard Deviation
And the maximum blend ratio:
Minimum Blend Ratio = Acceptable Level/Distance
As mentioned earlier, this is done for each of the three segmentation schemes. The overall maximum blend ratio is taken as the lowest of these. This is done for each of the demographic groups.
The effect of target sample size and acceptable likelihood
A total maximum blend ratio is computed based on the weighted sum of the individual demographic cells. Figure 8 shows the distribution of these total maximum blend ratios as a function of a and N.
Notice that this ratio decreases as a and N increase. As the tolerance, indicated by these factors, decreases, with increasing values of these parameters, the quantity of respondents that can be blended decreases.
We have chosen the targeted sample size to be 1,500 and used an a = 32 percent or one standard error. This corresponds to what we believe to be reasonable conditions for a typical mixed-source application. In the case of VOP and Peanut Labs, this allows an average maximum blending ratio of 18 percent, covering all demographic cells, though in reality the specific percentage will differ between the cells. Increasing the tolerance would result in a larger maximum blending ratio, as well as the reverse, should more conservative estimates be desired.
Variation within demographic cell
Figure 9 shows the distribution of maximum blend ratios across the demographic cells using averaged values. It ranges from 11 percent for the female 55+ to a high of 37 percent for the female 18-24.
Final blending model and maximum effect
Figures 10-12 show the effect of the blending process based on the three main segmentions. It is expected that there should not be any major differences between Valued Opinions Panel, and the blend, even though 18.8 percent of the blend is respondents from Peanut Labs. Figure 10 shows the results for the buyer behavior segments. While there are differences between the host and the blend, they are relatively minor.
Figure 11 shows similar results for the sociographic segments. Clearly, as previously noted, Valued Opinions Panel and Peanut Labs are very different. But the blend is very close to that of the original panel. The blend and Peanut Labs sample sets were significantly different at p<.01.
Figure 12 shows the results for the media usage segments with the same conclusions. The differences between the blend and the host are minor compared to that against the total for Peanut Labs. It is this similarity of characteristics that allows for the blend to be used as an extension of the original panel without major concern regarding consistency. The blend and Peanut Labs samples continued to be significantly different.
The effect of blending on survey-taking behavior
The blending procedure was designed to ensure that the structural segments of the blended sample remain statistically similar to the original panel when controlling for demography. However, the introduction of blended sample may result in differences with regard to survey-taking characteristics of the sample such as panel tenure, survey-taking hyperactivity and quality metrics. The changes that one can expect are detailed in Figures 13-15.
Figure 13 shows the results for performance, a measure of respondents’ susceptibility to “trap” questions, through which respondents’ engagement in the survey is tested. Three such questions were used. First, an instructional question where respondents were asked to enter a certain value. Those who entered an incorrect value received a mark for “failure to follow instructions.” Two other questions asked logically-identical but oppositely-worded questions regarding their quality of life and their preference for brand over price. An attentive respondent should give opposite answers to these questions and those who did not were coded as being “inconsistent.” As shown by the root mean squared error (RMSE) statistic, the blended sample was not significantly different from VOP in any measure of performance but was significantly different from the source sample set in all cases except “standard of living.”
There is evidence that changes in panel members’ tenure can cause shifts in data. In Figure 14, the comparison between the aging of panel participation distributions for blend, VOP and the Peanut Labs reference is shown.
The performance characteristics that were covered previously focused on the errors made by respondents and their tenure on panels. There is a third category of activities that are thought to possibly affect the quality of results. These are the participants who either speed through the survey (speeders) and those who give similar or identical values to blocks of questions in the surveys (straightliners). These respondents can be viewed as potential satisficers. In Figure 15, the distribution of satisficing behavior is shown. Based on the RMSE, the number of straightliners and speeders in the blended sample was not significantly different from VOP or Peanut Labs.
Detectably different
Here we introduce the concept of a minimum measurable difference. It serves as the minimum change in our metrics where we conclude that samples are detectably different: at any lesser change the populations are considered the same. This contrasts with the standard statistical interpretation where we simply determine that two populations differ, without a measure at which point that difference was achieved.
Social media participants represent a large potential opportunity to source respondents for market research purposes. They represent a different population of respondents from those typically found in online panels. By virtue of their difference and abundance, we must find ways to include them in our online research.
However, their difference is both a resource and a potential problem. The existing panels have been providing valuable data for years and a sudden inclusion of new respondents has the potential to create data inconsistencies that should be cautiously avoided. We have proposed a conservative and measured way of including these new sources in a granular fashion. Their inherent difference within each demographic cell dictates the maximum blending percentage we feel can comfortably be added to a host population of online panel respondents.
At this time, it is better to err on the conservative side when merging these respondents into existing panels. Thus we have incorporated worst-case scenarios involving sample size, income and the amount of statistically measured difference that we allow into our sampling populations.
The management of online samples is shifting from quota fulfillment to a concern for total sample frame. This type of approach is sensitive to the overriding philosophy that those who use these samples must be confident that the change they see in their data is real and not an artifact generated by shifts in the constituent elements of the sample source being employed. Sample providers have a responsibility to be transparent about their sample frame. It is only through clarity that research practitioners can understand how to interpret their data and it is only through that clarity that end users will know what reliance to place upon it.
Once methods are employed to assure quality they cannot be one-time credentials. In the best of worlds they are sensitive to changing social, political and economic conditions. As in all other quality metrics we do not consider the blending ratios to be static, therefore comparative analysis must be an ongoing endeavor.
References
Gittelman, Steven and Elaine Trimarchi (2010). “Online Research ... And All That Jazz! The Practical Adaptation of Old Tunes to Make New Music.” ESOMAR Online Research 2010.
Walker, Robert, Raymond Pettit and Joel Rubinson (2009). “A Special Report From The Advertising Research Foundation: The Foundations of Quality Initiative - A Five-Part Immersion into the Quality of Online Research.” Journal of Advertising Research 49: 464-485. 2009.