The risk of missing something important
Editor’s note: Peter DePaulo is an independent marketing research consultant and focus group moderator doing business as DePaulo Research Consulting, Montgomeryville, Pa.
In a qualitative research project, how large should the sample be? How many focus group respondents, individual depth interviews (IDIs), or ethnographic observations are needed?
We do have some informal rules of thumb. For example, Maria Krieger (in her white paper, “The Single Group Caveat,” Brain Tree Research & Consulting, 1991) advises that separate focus groups are needed for major segments such as men, women, and age groups, and that two or more groups are needed per segment because any one group may be idiosyncratic. Another guideline is to continue doing groups or IDIs until we seem to have reached a saturation point and are no longer hearing anything new.
Such rules are intuitive and reasonable, but they are not solidly grounded and do not really tell us what an optimal qualitative sample size may be. The approach proposed here gives specific answers based on a firm foundation.
First, the importance of sample size in qualitative research must be understood.
Size does matter, even for a qualitative sample
One might suppose that “N” (the number in the sample) simply is not very important in a qualitative project. After all, the effect of increasing N, as we learned in statistics class, is to reduce the sampling error (e.g., the +/- 3 percent variation in opinion polls with N = 1,000) in a quantitative estimate. Qualitative research normally is inappropriate for estimating quantities. So, we lack the old familiar reason for increasing sample size.
Nevertheless, in qualitative work, we do try to discover something. We may be seeking to uncover: the reasons why consumers may or may not be satisfied with a product; the product attributes that may be important to users; possible consumer perceptions of celebrity spokespersons; the various problems that consumers may experience with our brand; or other kinds of insights. (For lack of a better term, I will use the word “perception” to refer to a reason, need, attribute, problem, or whatever the qualitative project is intended to uncover.) It would be up to a subsequent quantitative study to estimate, with statistical precision, how important or prevalent each perception actually is.
The key point is this: Our qualitative sample must be big enough to assure that we are likely to hear most or all of the perceptions that might be important. Within a target market, different customers may have diverse perceptions. Therefore, the smaller the sample size, the narrower the range of perceptions we may hear. On the positive side, the larger the sample size, the less likely it is that we would fail to discover a perception that we would have wanted to know. In other words, our objective in designing qualitative research is to reduce the chances of discovery failure, as opposed to reducing (quantitative) estimation error.
Discovery failure can be serious
What might go wrong if a qualitative project fails to uncover an actionable perception (or attribute, opinion, need, experience, etc.)? Here are some possibilities:
- A source of dissatisfaction is not discovered - and not corrected. In highly competitive industries, even a small incidence of dissatisfaction could dent the bottom line.
- In the qualitative testing of an advertisement, a copy point that offends a small but vocal subgroup of the market is not discovered until a public-relations fiasco erupts.
- When qualitative procedures are used to pre-test a quantitative questionnaire, an undiscovered ambiguity in the wording of a question may mean that some of the subsequent quantitative respondents give invalid responses. Thus, qualitative discovery failure eventually can result in quantitative estimation error due to respondent miscomprehension.
Therefore, size does matter in a qualitative sample, though for a different reason that in a quant sample. The following example shows how the risk of discover failure may be easy to overlook even when it is formidable.
Example of the risk being higher than expected
The managers of a medical clinic (name withheld) had heard favorable anecdotal feedback about the clinic’s quality, but wanted an independent evaluation through research. The budget permitted only one focus group with 10 clinic patients. All 10 respondents clearly were satisfied with the clinic, and group discussion did not reverse these views.
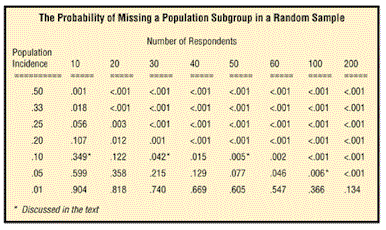
Did we miss anything as a result of interviewing only 10? Suppose, for example that the clinic had a moody staff member who, unbeknownst to management, was aggravating one in 10 clinic patients. Also, suppose that management would have wanted to discover anything that affects the satisfaction at least 10 percent of customers. If there really was an unknown satisfaction problem with a 10 percent incidence, then what was the chance that our sample of 10 happened to miss it? That is, what is the probability that no member of the subgroup defined as those who experienced the staffer in a bad mood happened to get into the sample?
At first thought, the answer might seem to be “not much” chance of missing the problem. The hypothetical incidence is “one in 10,” and we did indeed interview 10 patients. Actually, the probability that our sample failed to include a patient aggravated by the moody staffer turns out to be just over one in three (0.349 to be exact). This probability is simple to calculate: Consider that the chance of any one customer selected at random not being a member of the 10 percent (aggravated) subgroup is 0.9 (i.e., a nine in 10 chance). Next, consider that the chance of failing to reach anyone from the 10 percent subgroup twice in a row (by selecting two customers at random) is 0.9 X 0.9, or 0.9 to the second power, which equals 0.81. Now, it should be clear that the chance of missing the subgroup 10 times in a row (i.e., when drawing a sample of 10) is 0.9 to the tenth power, which is 0.35. Thus, there is a 35 percent chance that our sample of 10 would have “missed” patients who experienced the staffer in a bad mood. Put another way, just over one in three random samples of 10 will miss an experience or characteristic with an incidence of 10 percent.
This seems counter-intuitively high, even to quant researchers to whom I have shown this analysis. Perhaps people implicitly assume the fallacy that if something has an overall frequency of one in N, then it is almost sure to appear in N chances.
Basing the decision on calculated probabilities
So, how can we figure the sample size needed to reduce the risk as much as we want? I am proposing two ways. One would be based on calculated probabilities like those in the table above, which was created by repeating the power calculations described above for various incidences and sample sizes. The client and researcher would peruse the table and select a sample size that is affordable yet reduces the risk of discover failure to a tolerable level.
For example, if the research team would want to discover a perception with an incidence as low as 10 percent of the population, and if the team wanted to reduce the risk of missing that subgroup to less than 5 percent, then a sample of N=30 would suffice, assuming random selection. (To be exact, the risk shown in the table is .042, or 4.2 percent.) This is analogous to having 95 percent confidence in being able to discover a perception with a 10 percent incidence. Remember, however, that we are expressing the confidence in uncovering a qualitative insight - as opposed to the usual quantitative notion of “confidence” in estimating a proportion or mean plus or minus the measurement error.
If the team wants to be more conservative and reduce the risk of missing the one-in-10 subgroup to less than 1 percent (i.e., 99 percent confidence), then a sample of nearly 50 would be needed. This would reduce the risk to nearly 0.005 (see table).
 |
What about non-randomness?
Of course, the table assumes random sampling, and qualitative samples often are not randomly drawn. Typically, focus groups are recruited from facility databases, which are not guaranteed to be strictly representative of the local adult population, and factors such as refusals (also a problem in quantitative surveys, by the way) further compromise the randomness of the sample.
Unfortunately, nothing can be done about subgroups that are impossible to reach, such as people who, for whatever reason, never cooperate when recruiters call. Nevertheless, we can still sample those subgroups who are less likely to be reached as long as the recruiter’s call has some chance of being received favorably, for example, people who are home only half as often as the average target customer but will still answer the call and accept our invitation to participate. We can compensate for their reduced likelihood of being contacted by thinking of their reachable incidence as half of their actual incidence. Specifically, if we wanted to allocate enough budget to reach a 10 percent subgroup even if it is twice as hard to reach, then we would suppose that their reachable incidence is as low as 5 percent, and look at the 5 percent row in the table. If, for instance, we wanted to be very conservative, we would recruit 100 respondents, resulting in less than a 1 percent chance - .006, to be exact - of missing a 5 percent subgroup (or a 10 percent subgroup that behaves like a 5 percent subgroup in likelihood of being reached).
An approach based on actual qualitative findings
The other way of figuring an appropriate sample size would be to consider the findings of a pair of actual qualitative studies reported by Abbie Griffin and John Hauser in an article, “The Voice of the Customer” (Marketing Science, Winter 1993). These researchers looked at the number of customer needs uncovered by various numbers of focus groups and in-depth interviews.
In one of the two studies, two-hour focus groups and one-hour in-depth interviews (IDIs) were conducted with users of a complex piece of office equipment. In the other study, IDIs were conducted with consumers of coolers, knapsacks, and other portable means of storing food. Both studies looked at the number of needs (attributes, broadly defined) uncovered for each product category. Using mathematical extrapolations, the authors hypothesized that 20-30 IDIs are needed to uncover 90-95 percent of all customer needs for the product categories studied.
As with typical learning curves, there were diminishing returns in the sense that fewer new (non-duplicate) needs were uncovered with each additional IDI. It seemed that few additional needs would be uncovered after 30 IDIs. This is consistent with the probability table (shown earlier), which shows that perceptions of all but the smallest market segments are likely to be found in samples of 30 or less.
In the office equipment study, one two-hour focus group was no better than two one-hour IDIs, implying that “group synergies [did] not seem to be present” in the focus groups. The study also suggested that multiple analysts are needed to uncover the broadest range of needs.
These studies were conducted within the context of quality function deployment, where, according to the authors, 200-400 “customer needs” are usually identified. It is not clear how the results might generalize to other qualitative applications.
Nevertheless, if one were to base a sample-size decision on the Griffin and Hauser results, the implication would be to conduct 20-30 IDIs and to arrange for multiple analysts to look for insights in the data. Perhaps backroom observers could, to some extent, serve as additional analysts by taking notes while watching the groups or interviews. The observers’ notes might contain some insights that the moderator overlooks, thus helping to minimize the chances of missing something important.
N=30 as a starting point for planning
Neither the calculation of probabilities in the prior table nor the empirical rationale of Griffin and Hauser is assured of being the last word on qualitative sample size. There might be other ways of figuring the number of IDIs, groups, or ethnographic observations needed to avoid missing something important.
Until the definitive answer is provided, perhaps an N of 30 respondents is a reasonable starting point for deciding the qualitative sample size that can reveal the full range (or nearly the full range) of potentially important customer perceptions. An N of 30 reduces the probability of missing a perception with a 10 percent-incidence to less than 5 percent (assuming random sampling), and it is the upper end of the range found by Griffin and Hauser. If the budget is limited, we might reduce the N below 30, but the client must understand the increased risks of missing perceptions that may be worth knowing. If the stakes and budget are high enough, we might go with a larger sample in order to ensure that smaller (or harder to reach) subgroups are still likely to be represented.
If focus groups are desired, and we want to count each respondent separately toward the N we choose (e.g., getting an N of 30 from three groups with 10 respondents in each), then it is important for every respondent to have sufficient air time on the key issues. Using mini groups instead of traditional-size groups could help achieve this objective. Also, it is critical for the moderator to control dominators and bring out the shy people, lest the distinctive perceptions of less-talkative customers are missed.
Across segments or within each one?
A complication arises when we are separately exploring different customer segments, such as men versus women, different age groups, or consumers in different geographic regions. In the case of gender and a desired N of 30, for example, do we need 30 in total (15 males plus 15 females) or do we really need to interview 60 people (30 males plus 30 females)? This is a judgment call, which would depend on the researchers’ belief in the extent to which customer perceptions may vary from segment to segment. Of course, it may also depend on budget. To play it safe, each segment should have its own N large enough so that appreciable subgroups within the segment are likely to be represented in the sample.
What if we only want the “typical” or “majority” view?
For some purportedly qualitative studies, the stated or implied purpose may be to get a sense of how customers feel overall about the issue under study. For example, the client may want to know whether customers “generally” respond favorably to a new concept. In that case, it might be argued that we need not be concerned about having a sample large enough to make certain that we discover minority viewpoints, because the client is interested only in how “most” customers react.
The problem with this agenda is that the “qualitative” research would have an implicit quantitative purpose: to reveal the attribute or point of view held by more than 50 percent of the population. If, indeed, we observe what “most” qualitative respondents say or do and then infer that we have found the majority reaction, we are doing more than “discovering” that reaction: We are implicitly estimating its incidence at more than 50 percent.
The approach I propose makes no such inferences. If we find that only one respondent in a sample of 30 holds a particular view, we make no assumption that it represents a 10 percent population incidence, although, as discussed later, it might be that high. The actual population incidence is likely to be closer to 3.3 percent (1/30) than to 10 percent. Moreover, to keep the study qualitative, we should not say that we have estimated the incidence at all. We only want to ensure that if there is an attribute or opinion with an incidence as low as 10 percent, we are likely to have at least one respondent to speak for it - and a sample of 30 will probably do the job.
If we do want to draw quantitative inferences from a qualitative procedure (and, normally, this is ill advised), then this paper does not apply. Instead, the researchers should use the usual calculations for setting a quantitative sample size at which the estimation error resulting from random sampling variations would be acceptably low.
Keeping qualitative pure
Whenever I present this sample-size proposal, someone usually objects that I am somehow “quantifying qualitative.” On the contrary, estimating the chances of missing a potentially important perception is completely different from estimating the percent of a target population who hold a particular perception. To put it another way, calculating the odds of missing a perception with a hypothetical incidence does not quantify the incidences of those perceptions that we actually do uncover.
Therefore, qualitative consultants should not be reluctant to talk about the probability of missing something important. In so doing, they will not lose their identity as qualitative researchers, nor will they need any “high math.” Moreover, by distinguishing between discovery failure and estimation error, researchers can help their clients fully understand the difference between qualitative and quantitative purposes. In short, the approach I propose is intended to ensure that qualitative will accomplish what it does best - to discover (not measure) potentially important insights.