Formulating insights
Editor's note: David Burns is principal of San Francisco-based Seal Rock Research.
Have you encountered “gotcha” questions such as, “How can this research mean anything if it’s not statistically significant?” and “How can you conclude anything with so few participants?” Qualitative research has an image among some clients and others as soft, subjective and unscientific. This image is true only to the extent that we as qualitative researchers neglect the scientific underpinnings of our profession.
In this article I will show the statistical basis for qualitative sample selection in issue discovery research. I hope this article will encourage other researchers to give more attention to the scientific foundations of qualitative research.
Did not anticipate
Qualitative research is unequalled in its ability to uncover facts that we or our clients did not anticipate. I am calling these facts issues and the process of uncovering them issue discovery.
An issue could be that a product is too thick or heavy, that a Web interface makes it hard to discover an important feature, that an advertising message has unwanted sexual connotations or that a company is perceived as arrogant. Issues do not have to be negative: Qualitative research can uncover positive attributes, perceptions and associations that marketers weren’t aware of.
We can use mathematical formulas to help select appropriate sample sizes for issue discovery. These formulas can also determine the effectiveness of the sample used for a particular project. Usability researchers developed these formulas but they are applicable to a wide array of qualitative research where issue discovery is an important goal. The formulas are simple and easy to implement in a spreadsheet.
The variables
In a qualitative project, three key facts are connected to issue discovery. These facts form the variables of our equations. They are:
-
How common must an issue be to be of concern? This is the incidence of the issue. I’ll call this variable i.
-
How powerful do we want our study to be in finding those issues? This is the percent of issues with incidence i we want to discover. I’ll call this variable p.
-
How many respondents will participate in our study? This is n. In some cases, we already know what n is and want to know how much issue discovery power our study will have. In other cases, we know how powerful we want our study to be and we select n to satisfy our criteria.
Let’s look at i and p in detail.
The incidence of an issue, i, determines how interested we are in it. If an issue only affects 1 percent of the study population, we may not need to know about it or it may be impractical to discover it in a qualitative project. If half or more are affected, we definitely need to know and it will be easy to discover. For the purposes of most qualitative projects, issues affecting 10 to 20 percent of the population are certainly important enough that we should try to discover most of them.
The power of a study, p, is determined by the number of participants and the incidence of the issues we wish to discover. Power is also affected by the knowledge, skill and effort of the researcher, but we can consider that a constant.
Power can be thought of in two ways. Formally, it is the probability that we will discover an issue of incidence i in a study of size n. In general qualitative research, where there may be many issues to discover, it may be more useful to think of p as the percent of issues of incidence i that we can expect to discover. That does not mean we will discover exactly p percent of issues with incidence i, any more than our expectation that half of our coin tosses will be heads means that five of any 10 tosses will come up heads.
For issues more common than i, we can expect to discover a higher percentage than p. For issues that are less common, we expect to discover a lower percent.
The formulas
The formula for finding the power of a study, given the incidence and cardinality, is:
p = 1 - (1-i)n
(Formula 1)
This formula is best known from its presentation by Jakob Nielsen and Thomas Landauer in 19831.
Let’s look at an example. If a small qualitative project has 10 participants and we are interested in issues affecting 25 percent or more of them, what proportion of those issues are we likely to discover?
Plugging in 10 for n and .25 for i, we get:
p = 1 - (1 - .25)n
or p = 1 - (.75)n = 94%
Since p is 94 percent, a sample size of 10 means we can expect to capture over nine in 10 of all issues that affect 25 percent or more of our study population.
This is interesting, but often what we really want to do is find a sample size that will give us the resolving power we need in discovering issues. That is, given our choice of i and p, what should n be? I have derived the following formula from an example shown by Jeff Sauro2:
n = log (-(p-1)) / log(1-i)
(Formula 2)
Let’s look at an example. Suppose we want at least a nine-in-10 chance of capturing issues that affect as few as 10 percent of our study population. How many people do we need to recruit?
Nine in 10 is 90 percent; that’s our p. The incidence of concern is 10 percent; that is i. So:
n = log(-(.9 - 1)) / log(1-.1)
or n = log(.1)/log(.9)
or n = 21.85
We can’t recruit .85 of a person, so n has to be 22.
More about i
I described the incidence, i, as the percent of the population affected by an issue. In reality, i can only describe the percent of the population who will expose the issue to us in our study. People affected by an issue might fail to expose it in the course of a study for a number of reasons: embarrassment; lack of time; they don’t think it’s important; the moderator’s promptings never brought it up, etc. Conversely, a respondent might expose an issue that she herself is not affected by but thinks someone else might be. For example, a right-handed person might point out defects in a product design that would only affect left-handed people. Thus i should really be thought of as
i - p(miss) + p(unaffected)
where p(miss) is the probability we will miss the opportunity to discover an issue from an affected individual, and p(unaffected) is the probability that we will discover it from an unaffected individual.
This is where knowledge, skill and experience come into play. The design and execution of a study profoundly influence the likelihood of missing an issue or discovering it from unaffected participants.
Example 1
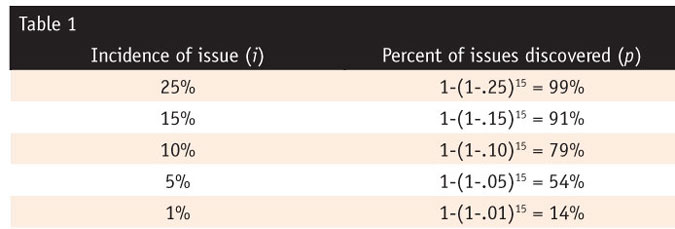
Let’s look at a small qualitative project of 15 in-depth interviews. How much issue-discovery power does this study have?
Using our first formula with 15 for n and plugging in different values for i, I generated Table 1.

Our study has a better than 90 percent chance of detecting any issue affecting 15 percent or more of the study population. It has nearly a four-in-five chance of finding an issue affecting as few as 10 percent. For less-common issues we will need a larger sample size: Our chance of finding any particular issue affecting 1 percent of the population is only 14 percent.
Example 2
Suppose we are working on a project with multiple segments and we want to ensure that at least three-quarters of people in each segment will have no issues with our messaging. How many people should we recruit in each segment?
Using our second formula with i at 25 percent, we can see how many people we need to recruit at each level of confidence we might wish to achieve (Table 2).

There seems to be a sweet spot at 11 recruits with 95 percent confidence, but if the budget allows, we might be tempted to go to 16 recruits and 99 percent confidence.
Make us more confident
Qualitative research consultants may not frequently need to use these formulas. As the examples show, many qualitative projects have ample issue discovery power, assuming appropriate segmentation. But knowing the scientific basis for qualitative sample size selection gives us a framework for thinking and talking about the qualitative sample sizes we choose or recommend. This can help make us and our clients more confident in the qualitative research we conduct.
References
1 Nielsen, J., and Landauer, T.K. (1993). “A mathematical model of the finding of usability problems.” Proceedings of INTERCHI 93, 206-213. New York, NY: ACM.
2 Sauro, Jeff. (March 8, 2004). “Deriving a Problem Discovery Sample Size.” Retrieved fromwww.measuringusability.com/qualitative_
sidebar.htm on June 8, 2011.