Editor’s note: Randy Hanson is a senior research manager with the St. Louis division of Maritz Marketing Research, Inc. He is a Phi Beta Kappa graduate of the University of Missouri where he received an M.A. in statistics.
Factor analysis is a generic term for techniques that analyze interrelationships among variables. Its purpose is to reduce a large set of variables to a smaller set of unifying concepts, or "factors." Factor analysis accomplishes this reduction through a statistical model that attempts to explain the correlation between variables. Many widely available data analysis packages such as SAS® and SPSS® contain programs to conduct factor analysis.
In marketing research studies, ratings are often collected on a large number of products, attributes, attitudes or behaviors. Usually, it's reasonable to assume these ratings are correlated because the items measured are typically different facets of a few common, underlying dimensions.
For example, assume respondents are asked to rate a product or service on 20 attributes. Several of the attributes may actually measure the same dimension, such as quality, cost, or usefulness. While these dimensions are neither well-defined nor easily measured, factor analysis can help determine the factors which underlie the 20 original variables. Factor analysis can both simplify the description and increase the understanding of complex phenomena such as purchase intentions and consumer evaluations.
Four steps
There are usually four steps in a factor analysis: 1. Compute the correlation matrix; 2. Extract the factors; 3. Rotate the factors; and 4. Calculate factor scores.
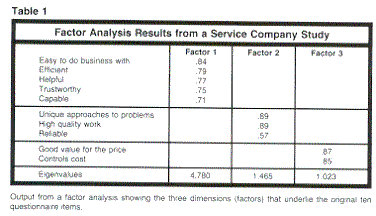
These steps will be discussed in the context of a specific example: A service company wants to know how customers perceive its organization and competitor companies. Customers are asked to rate each company on a list of 10 attributes. Results of this factor analysis are shown in Table 1.
 |
Step one: Once the data are collected, the correlation matrix is computed and examined to determine if a factor analysis is appropriate. If nearly all the correlations are small, there is probably not much point in carrying out the analysis. The correlation matrix can also provide a preview of the factor analysis results by identifying separate groups of highly correlated variables.
Step two: The extraction phase of factor analysis requires several decisions by the analyst. First, a method of factor extraction (principal components, principal axis factoring, maximum likelihood, or a host of others) must be selected. In our example, the widely-used method of principal components analysis is used. Second, the number of factors to be retained must be decided. The most frequently used criterion is to keep all factors with eigenvalues greater than one. (An eigenvalue is simply the portion of total variation explained by each factor). In our example, the first three factors are retained because their eigenvalues are greater than one.
Step three: The factor solution is then rotated to make the factors more interpretable. Choices include varimax, quartimax, equamax and oblique rotation, with varimax being the most frequently used. The rotated factor analysis results for our example, based on varimax rotation, produce the factor loadings and eigenvalues for our 10 original attributes (see Table 1). Factor loadings show the degree of association of each attribute with each underlying factor and range from -1 to + 1 (only loadings with absolute values greater than .5 are shown in the table).
Naming factors
At this point, some time should be spent naming factors. This process will highlight the criteria used by customers to evaluate the companies. Looking at the attributes with higher factor loadings we might call Factor One in our example, "The Basics," or "Comfort Level;" Factor Two, "Quality," or "Status," and Factor Three, "Money's Worth." Thus, the company's future advertising and sales presentations may be more effective if they stress "The Basics," "Quality," or "Money's Worth."
Step four: After naming the rotated factors, scores for each respondent are calculated. The factor scores are simply summary ratings for each underlying factor. We now have three variables per customer for analysis instead of the original 10. This reduced set of data can then be used in a variety of subsequent analyses.
For example: 1. Customers can be segmented (clustered) based on factor scores to reveal subgroups with similar evaluative styles; 2. If a nonoblique rotation is used, the factor scores can serve as independent variables in a subsequent regression analysis, and 3. The factor scores can be used as input for a factor-based perceptual map.
Technique usefulness
There are a growing number of factor analysis practitioners who have doubts about the general usefulness of the technique. While factor analysis is relatively sound from a mathematical perspective, it is criticized for:
- Misapplication: The question here is whether underlying factors exist at all. While a factor analysis can be applied to any database, it may not be appropriate. The evidence suggests the concept of factors may be valid within psychology but is, in other circumstances, open to debate. Separate from this, the researcher may use factor analysis to "group" attributes as they already exist, not to discover underlying factors. In these situations, clustering based on variables is a more appropriate technique.
- Ambiguity: There is a great deal of subjectivity in choosing the number of factors to retain, the extraction method and the rotation method. Because of this, two honest researchers analyzing the same data independently may find different factors and reach divergent conclusions. At worst, this ambiguity can be used by an unscrupulous analyst to try different combinations of methods until a preconceived hypothesis comes up. A defensible solution to this "data snooping" is to set objective standards and procedures before the data are analyzed.
In summary, factor analysis is a tool to be included in every marketing researcher's repertoire. It is not, however, a panacea. Factor analysis is a useful technique when conditions are appropriate, when it is conscientiously applied and most importantly, when it provides a deeper and clearer understanding of the data.