No-shows? No problem
Editor's note: Pete DePaulo is an independent moderator and research consultant based in suburban Philadelphia. He wishes to thank Robert Kahle (Kahle Research Solutions), Anndel Martin (Opinions Unlimited), Barbara Rosenthal (Rosenthal Qualitative Research), and Merrill Shugoll (Shugoll Research) for their feedback when this paper was presented at the 2001 annual conference of the Qualitative Research Consultants Association, and to the QRCA Field Committee.
If you do qualitative research, it happens once in a while: too many no-shows. You may have recruited, for example, 12 qualified people for eight to 10 to show for your focus group, but fewer than eight arrive. Now, if there was a blizzard, unusual traffic jam, or some other "act of God" keeping recruits away, well, those things just happen. Nobody is blamed.
But what if there is no good reason for the shortfall? The weather is okay, the traffic is normal, the local team is not in the playoffs, the recruit is routine (e.g., adult users of a common household product), the incentive is the going rate, and the screening questions are innocuous.
Under these circumstances, you might presume that someone, such as the recruiter, must have screwed up - particularly if the number of show-ups is way off (e.g., if you were supposed to get at least eight respondents but only five arrive). At best, faces are red. At worst, heads roll. The moderator may lose her client, the facility manager may lose the moderator's business, and the recruiter may lose his job.
Can we be sure that someone is at fault?
But are we really sure that someone messed up? Or, could the "under-show" have been simply bad luck - a sheer coincidence? After all, if you are handed a new pair of dice and get "snake eyes" the first time you roll them, you do not immediately conclude that the dice are loaded. There is a one in 36 chance of getting snake eyes with honest dice (1/6 X 1/6 = 1/36). But what if you roll the dice four times and get snake eyes every time? The probability of that happening purely by chance is, literally, less than one in a million (1/36 X 1/36 X 1/36 X 1/36 = 1/1,679,616). Now you have serious doubts about the design of the dice.
By the same logic, we should not consider blaming a low number of show-ups on lax recruiting, unless the possibility of the outcome occurring by coincidence is very small and there was no act of God. But how can we figure the likelihood of an under-show happening purely by chance?
Actually, it's easy. Electronic spreadsheets such as Excel have a binomial distribution function, which can calculate the probabilities we need. Similar probabilities, by the way, are helpful in deciding the sample size needed for qualitative research (see Quirk's, December 2000, page 22, or visit www.quirks.com and enter Article Quick Link number 636).
Even if math is not your cup of tea, please read on. You need not know what "binomial" means or how the calculations work. The only catch is that we must make an assumption about the overall show rate (the percent of recruits who can be expected to show up), which must be plugged into the binomial formula.
So, what are typical show rates? To get some show-rate estimates, I consulted with the Field Committee of the Qualitative Research Consultants Association (QRCA). The committee members include facility owners and other consultants interested in issues such as recruiting. The consensus was that 80 percent is about an average show rate (i.e., eight of 10 recruits typically arrive), 90 percent is a very good rate, and 50 percent (teenagers, perhaps) is a really bad rate. Later, committee chair and facility owner Anndel Martin (of Opinions Unlimited) polled 15 GroupNet facility members, who reported that typical show rates range from 75 percent to 85 percent. Another facility owner, Merrill Shugoll, looked at the records of a random sample of 100 groups conducted at Shugoll Research. Of all the recruits for those groups, 80.2 percent showed up.
This range of 75 percent-85 percent makes sense considering that in a typical job, 12 respondents are recruited for eight to 10 to show. If nine people show up, they are 75 percent of the 12 recruits; if 10 showed, they comprise 83 percent.
Probability of n recruits showing up
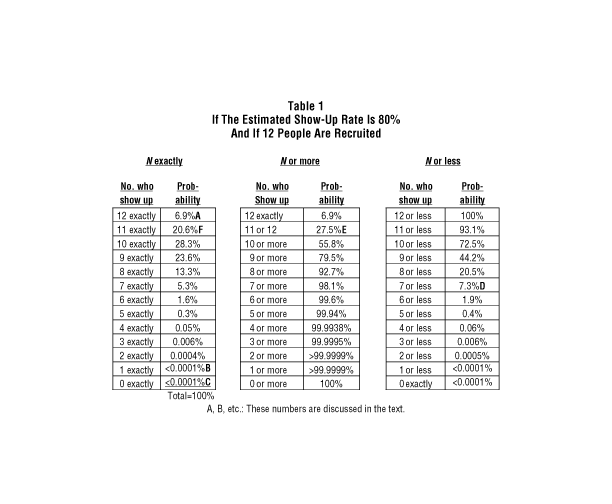
Now we are ready to look at some probabilities. Table 1 reveals the results of Excel's binomial calculations with 80 percent as the presumed overall show rate (i.e., on average, eight in 10 would arrive) and 12 as the presumed number of people recruited.
 |
For example, the probability of all 12 recruits showing up is close to 7 percent. (See "A," 6.9 percent, in the upper left area of Table 1.) Thus, out of every 100 focus groups for which the expected show-up rate is 80 percent and 12 individuals are recruited - and no act of God alters the show rate - attendance would be perfect for approximately seven groups.
At the other extreme, the likelihood of either one person showing up or nobody showing up is less than 0.0001 percent (see "B" and "C" in Table 1) - which is the proverbial "one in a million." If there were no blizzard, unusual traffic jam, or any other act of God, then it would seem extremely likely that someone must have screwed up. Of course, we can't be absolutely certain that if fewer than two recruits show up then something must have gone wrong. After all, someone does win the million-dollar lottery. Still, if there was no act of God, then the most likely explanation obviously would be human error.
The next two columns in the table show what we really need to know: the chances of getting more or less than some meaningful number of show-ups, e.g., fewer than eight if we are recruiting for at least eight to show. As revealed in the last column, the probability of seven or fewer showing up is approximately 7.3 percent ("D" in Table 1). This was calculated by summing the specific probabilities for outcomes below eight in the second column. Let's call it the risk of a disappointment.
Another type of "risk" is that we might have to pay for "over-shows." If we will seat a maximum of 10 respondents (some moderators prefer to set a lower limit), and more than 10 show up, we pay the extras and send them home. The middle section of the table above shows that with an 80 percent show-up rate and 12 recruits, the overpayment risk is 27.5 percent ("E" in Table 1), which is the sum of the probability of getting exactly 12 show-ups (6.9 percent) plus the probability of getting exactly 11 show-ups (20.6 percent, which is "F" in Table 1). Of course, you may regard over-shows as a benefit instead of a risk, because you can pick and choose the most desirable participants out of your pool of show-ups.
The payoff from improving the show rate
Figure 1 reveals the importance of doing whatever can be done to improve the overall show-up rate - such as hiring recruiters with the ability to gain a firm commitment, persuading the recruits that they are likely to enjoy the discussion, paying a sufficient incentive, writing an effective follow-up letter with easy directions, and making confirmation calls.
 |
The main message from Figure 1 is that a small change in the overall show-up rate can make a big difference in how many happy or unhappy clients you have. Consider, for example, the thick solid line revealing the probability of getting seven or fewer show-ups out of 12 people recruited. The probability of that happening with an overall show rate of 80 percent is our now-familiar 7 percent chance of getting fewer than eight show-ups (see point G in the chart). The next point along this line reveals that if you can improve the overall show rate just 5 percentage points (from 80 percent to 85 percent), then the chance of getting seven or fewer show-ups drops to 2 percent (point H). That means that if you do 100 groups with these specs, you probably would suffer only two disappointing outcomes instead of seven. Looking at the positive side of the coin, the upper dotted line shows that the percent of over-shows (more than 10 show-ups) rises from 27 percent (J) to 44 percent (K) as a result of improving the show-up rate from 80 percent to 85 percent.
Think of what these differences could mean for client satisfaction: fewer clients would be upset by under-shows, and more would be delighted by over-shows from which to pick and choose.
Now let's look at the downside risk of letting your overall show rate fall, if, for example, you fail to place confirmation calls or hire less-skilled recruiters. If the overall rate drops from 80 percent to 70 percent, the probability of a disappointment (seven or fewer show up) quadruples from 7 percent to 28 percent (see point L). Moreover, the chance of a "disaster" (five or fewer show up) rises from near zero to 4 percent (M). Meanwhile, the percentage of groups with delightful over-shows drops from 27 percent to 9 percent (N). Imagine the serious consequences for your reputation and business.
The payoff from recruiting one or two more people
Besides increasing your overall show-up rate through better recruiting, another way of avoiding the risk of too few show-ups is simply to recruit more people to begin with - 13 or 14 instead of 12, for example. Table 2 shows the results of recruiting X number of people under three different overall show-up rates.
Let's start by looking at the cell for 12 people recruited under circumstances where the overall show rate of is 80 percent. Again, the table shows our old familiar 7.3 percent risk of fewer than eight persons showing up. One interesting new insight is that recruiting just one more person (13 instead of 12) goes a long way, cutting the risk of fewer than eight shows by more than half (from 7.3 percent to 3.0 percent). Adding yet another recruit (total=14) cuts the risk to nearly one in 100 (1.2 percent).
Reducing the risk to a tolerable level
What if we want to be virtually certain of getting at least eight people in the group (except for acts of God)? Table 2 suggests three ways of reducing the risk of this embarrassment to less than 0.1 percent (i.e., less than one in a thousand):
- Improve your recruiting procedures to the point where your overall show rate is 90 percent, and then recruit 13 people.
- Maintain an average show rate of 80 percent, and recruit 17 individuals.
- Cheapen your recruiting so that your show-up rate drops to 70 percent, but use the savings to recruit 21 people. (I do not recommend this.)

Table 3 uses a more efficient layout to address the question of how to attain a tolerably low level of risk. This table also includes show-up rates as low as 50 percent for those readers with the unenviable task of targeting the most unreliable respondent populations.
Researchers differ in their tolerance of risk, so your first step in using Table 3 is to decide what level of certainty to shoot for. Do you want, for example, to reduce the risk of an embarrassment to less than 1 percent, or are you willing to gamble with risks of 5 percent or more?
 |
Suppose you can tolerate a 5 percent risk of getting fewer than eight show-ups. Table 3 shows that if you believe your recruiting is savvy enough to deliver 90 percent of recruits to the facility, then you need only recruit 11 people to a group. On the other extreme, if you fear that your ornery target consumers have only a 50 percent likelihood of showing up, then you had better recruit 23 of them. If you want to bring your risk of an under-show below 1 percent, you would need 12 recruits, assuming a 90 percent overall show-up rate and 27 recruits, assuming a 50 percent overall rate.
What if you are doing a mini group and you want at least five to show? See Table 4.
Again, the importance of fine-tuned, reliable procedures for gaining commitment from recruits is apparent, even if you only want a mini group. Table 4 shows that with a 90 percent show-up rate, you only need eight recruits to reduce the chance of fewer than five show-ups to less than 1 percent. If your show-up rate is 50 percent, however, then you must more than double the number of recruits (to 19) for the same degree of assurance.
 |
If you need a different set of numbers
Inevitably, the numbers in this article will not meet the needs of all readers interested in no-show probabilities. If, for example, your client would be disappointed with fewer than 10 in the group, then you would need a table with 10 as the magic number rather than eight or five as I have provided here. That's no problem. Just do your own spreadsheet calculations - it's an easy one-liner. In Excel, the formula for calculating the probability of getting N or fewer showing up is =BINOMDIST(N,R,E,TRUE), where R is the number to be recruited and E is the expected show-up rate, which you enter as a proportion (e.g., "0.8" rather than "80 percent"). TRUE tells Excel that the probability you want is for getting "N or less." (Substituting FALSE gives you the less-useful probability of getting exactly N showing up.)
How to use these probabilities
Moderators and clients may use these probabilities in deciding how many people to recruit or in evaluating a recruiter after a disappointing number of show-ups. Of course, other factors ought to be considered besides these probabilities, e.g., the vendor's past track record. You might not let a bad number of shows with a probability of, say, 2 percent stand in the way of doing business with an otherwise reliable facility. However, if the probability was more like one in a thousand, you probably should consider the possibility that the facility's quality is slipping.
At the 2001 QRCA conference there was a session on this topic. Participants offered a number of practical suggestions for avoiding or dealing with the problem of too few recruits showing up. Here are just a few of the many ideas. Barbara Rosenthal described supportive, open communication, e.g., "What can we do to ensure that at least eight show up?" Anndel Martin recommended that the facility and client should agree up front on what the charges would be in case of an under-show. When a serious under-show does happen, Bob Kahle's practice is to call and interview the no-shows, not only to salvage data from them but also to discover why they didn't come. Merrill Shugoll added that if you are using a facility for the first time and get an under-show, call colleagues who have used the facility to see if it has been dependable for them.
Facilities or recruiters may use these probabilities in deciding whether to offer some kind of guarantee. They would want to assure their clients of a certain number of respondents showing up only if the probability of getting fewer than that number by sheer bad luck is sufficiently low. Also, if a client argues for saving budget by reducing the number recruited or the incentive offered, the facility or recruiter could respond by citing the potentially high risk of too few respondents showing up.
Generally, the analyses described here suggest that facilities and recruiters should consider investing to improve their procedures for motivating qualified recruits to show up, because, as illustrated in Figure 1, a small improvement in the show rate can markedly cut down on the incidence of client disappointment. Another implication is for the client: If there is reason to believe that the target respondents may be any less reliable in showing up, then the client should be willing to pay for one or more additional over-recruits.
Of course, a high show rate or large number of over-recruits cannot avoid poor outcomes due to unusual weather, traffic, or events. Nevertheless, increasing your show rate or upping the number of recruits can cut down substantially on the kinds of under-shows that are the most likely to alienate the client: those that happen when there is no apparent act of God to blame.