Editor's note: Lori Cook is a senior research analyst at Blue Cross Blue Shield of Maine, Portland.
This article is the first in a three-part series designed to provide real-world business examples of the effective use and application of research and statistical tools for supporting resourcing and priority-setting decisions. Each of the three articles in the series provides a summary review and example of how marketing research, when approached as a credible discipline and with a clear view of specific decision support needs, can very effectively shape executive decision making.
This article reviews "effect size" statistical testing tools as a means for assessing meaningful research outcomes; it focuses on successes using measures of "effect size" - in lieu of or in addition to statistical significance testing - to effectively demonstrate quality improvement and impact of customer satisfaction-based interventions.
Assessing research outcomes: statistically significant vs. meaningful differences
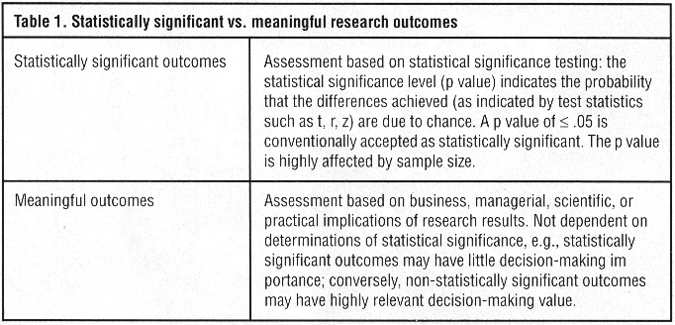
Organizations implementing quality improvement programs often use customer satisfaction survey research to track the effectiveness of improvement activities and interventions. Typically, determinations of program effectiveness (e.g., change from baseline to re-measure, or differences between independent groups) are based on statistical significance testing of research results. For example, z-tests or chi-squares are used to determine the statistical significance of the difference between proportions, whereas t-tests are used to determine statistically significant differences between means. Statistical significance tests such as these indicate the probability that research outcomes can reasonably be attributed to the program interventions, or whether they are simply due to chance. "Statistically significant" results can then be interpreted to mean that the program interventions have been successful, while non-statistically significant results indicate that the program interventions have not been successful. 1
For effective interpretation and application of such research results, it is important to note one of the limitations of traditional statistical significance testing: statistical significance is highly dependent on sample size (that is, the opportunities for achieving statistically significant results increase as sample size increases, and decrease as sample size decreases). Therefore, two studies with similar results may yield very different outcomes when statistical significance testing is applied, if the sample sizes used in the studies are different.
Because of this dependence on sample size, "statistically significant results" cannot always be equated with "meaningful results" (i.e., results that have important business, managerial, or scientific implications). It is possible for a large-sample study to have statistically significant results that do not reflect "meaningful" change or difference; conversely, it is possible for a small sample study to yield "meaningful" results without "statistical significance." D. Kenny (1987), in a discussion of this issue, gives the following example:
"Statistical significance cannot be equated with scientific significance because statistical significance depends on theoretically unimportant factors such as sample size. For example, consider two studies that attempt to reduce cigarette smoking. It is possible for the t statistic for one study to be 8.433, yet the treatment reduces cigarette smoking by two cigarettes. Whereas in second study the t statistic could be only 2.108, yet the program reduces the level of the smoking by 20 cigarettes. This could happen if the first study has 16,000 subjects, the second only 10 subjects....." (p. 211).

For the application of research results to have the greatest impact and value for decision support needs, assessment of research outcomes should therefore not be limited to determinations of statistical significance; consideration should also be given to the "meaningfulness" or practical importance of the outcomes. These two assessment dimensions are summarized in Table 1.
Assessing meaningful outcomes: effect size statistics
To effectively assess meaningful outcomes, a metric other than statistical significance testing is useful, one that measures the magnitude of a result, rather than the probability that the result is due to chance.
The most commonly used metric to evaluate the magnitude of an outcome is "effect size" (Cohen, 1988), or the "strength of an effect as opposed to its p value" (Kenny, 1987). There are several different test statistics for effect size, including:
- d (for measuring the effect size difference between two means)
- h (for measuring the effect size difference between two proportions)
- Fisher's Z (for measuring the association between two continuous variables)
Effect sizes are generally categorized as small (effect size = .2), medium (effect size = .5) and large (effect size = .8), corresponding to correlations of .1, .3, and .5, respectively (Cohen, 1988). Measures of effect size are commonly used in conjunction with significance testing in power analysis (an analytic method of determining how large a sample is needed to detect the effect of an intervention). Effect size is also one of the metrics of meta-analysis (i.e., the statistical integration of results of independent studies).
As noted earlier, an attribute of effect size statistics that distinguishes them from traditional significance tests is that they are not dependent on sample size. That is, the degree of difference or change required to reach a particular effect size remains the same regardless of sample size, while the degree of difference or change required for statistical significance increases as sample size decreases. Consider the following hypothetical example of a customer satisfaction survey result:
Sixty percent of respondents answer "Yes" to the question: "Overall, are you satisfied with the customer service provided by [name of organization]?"
If a quality improvement goal is to increase this percentage at remeasure so that the increase is statistically significant (as measured by a z-test), it would take an increase of 5 percentage points (to 65 percent) for a sample size of 1,000; however, it would take an increase of 19 percentage points (to 79 percent) for a sample size of 50.
In contrast, if a quality improvement goal is to increase this percentage at remeasure so that the increase meets the threshold for a minimum effect size (h = .2), the increase needed is 10 percentage points (to 70 percent), whether the sample size is 50 or 1,000.
Therefore, because effect size statistics are not dependent on sample size, and have a consistent measurement interpretation (i.e., small, medium, and large), they can provide a standardized context for interpreting "meaningful" results above and beyond statistical significance testing.
Effect size calculations
Calculations for d2, h, and Fisher's Z are provided in Table 2. As noted previously, results of each can be interpreted as "small" (.2) medium (.5) or large (.8).

Application
Example 1
Health plans use effect size statistics in quality improvement programs, both for goal-setting and for demonstrating improvement and impact of satisfaction-based interventions. Effect size testing has been found to be particularly useful for providing direction in small-sample studies, used in lieu of or in addition to statistical significance testing; this method has been validated and accepted by external accrediting organizations.
For example, the ACME Health Plan conducts an annual managed care member satisfaction telephone survey among a random sample of managed care members. This survey is used both to establish measurement baselines for new quality improvement initiatives and to track effectiveness of ongoing quality interventions.
One such intervention related to member experiences with claims processing. ACME researchers established an intervention goal to maximize the percent of members (based on survey results) who are "satisfied with getting their claims paid for." However, because this measure could be tracked only among a subset of survey respondents (i.e., those with claims), the small sample size precluded the use of statistical significance testing for feasible goal-setting and tracking. For example, in order to demonstrate "statistically significant improvement," an increase of 9 percentage points in those reporting "satisfaction with getting claims paid for" would have been needed. ACME researchers chose to use effect size testing to set more achievable goals (with the goal set at achieving a reduction that would meet the minimum threshold for a small effect size) and for tracking the impact of interventions.
To illustrate the impact of using effect size for ACME's goal-setting, the table below presents a comparison of the increase needed from baseline (Year 1) to remeasure (Year 2) to achieve: a) statistical significance, and b) small effect size, in ACME's claims processing satisfaction rating.

As the table indicates, the percent of members "satisfied with getting claims paid for" would need to increase from 90 percent to 99 percent (an increase of 9 percentage points) for the increase to be statistically significant (for n = 50), but would only need to increase from 90 percent to 96 percent (an increase of 6 percentage points) for the increase to reach the minimum threshold for a small effect size.
At ACME's survey remeasure point (Year 2), a comparison to the Year 1 baseline results demonstrated an increase in the percentage of members reporting "satisfaction with getting claims paid for" that did meet the criteria of a .2 (i.e., small) effect size. Ongoing trending of the data is used to demonstrate sustained improvement.
Example 2
ACME Health Plan conducts an annual physician-specific member satisfaction survey among a small random sample of patients for physicians who are being credentialed in the upcoming year (n = 24 respondents per physician). Because of the small sample sizes, using statistical significance testing to trend physician scores over time does not yield actionable information (since such testing is only sensitive to very large changes). Therefore, effect size testing has been found to be useful in certain instances (i.e., particularly with physicians who may be scoring below-average) to demonstrate performance improvement over time. As an example, Table 4 presents the patient satisfaction ratings for a hypothetical Physician X in 1997 and 1999:

The 8 percentage point increase in Physician X's satisfaction scores (from 80 percent to 88 percent) is not statistically significant, but does meet the minimum threshold for a small effect size. Due to the small sample size, an increase of 18 percentage points (from 80 percent to 98 percent) is required for the increase to be statistically significant.
Conclusion
This article's review of "effect size" statistical testing tools as a means to demonstrate quality improvement and the impact of customer satisfaction-based interventions illustrates how researchers can effectively leverage these tools for their organizations. However, despite the usefulness of this technique, this article does not mean to suggest that it should replace statistical significance testing in a researcher's arsenal of tools. In addition, you must also consider the challenge of communicating and establishing credibility for this approach among senior management or other organizational end-users who may not be versed in statistical methods.
Likewise, researchers need to continually consider the "real world" business implications regarding whether or not observed differences in the data - even if statistically significant or able to satisfy an effect size threshold - are sufficiently important and actionable for the organization. Relevant and effective decision support always starts with a clear understanding of the likely and possible business scenarios faced by executives. Underlying a researcher's effectiveness and credibility is the ability to understand the environment in which they are introducing technical tools.
References
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences , 2nd Edition. New Jersey: Lawrence Erlbaum Associates.
Judd, C.M., Smith, E.R., & Kidder, L.H. (1991). Research Methods in Social Re lations, 6th Edition. Fort Worth: Holt, Rinehart and Winston, Inc.
Kenny, D.A. (1987). Statistics for the Social and Behavioral Sciences. Boston: Little, Brown and Company.
Notes
1 Although survey research designs typically do not meet all the scientific criteria for inferring a causal relationship between the intervention and the outcome, the probability value of these test statistics (i.e., the statistical significance level or p value) provides protection from Type I errors (i.e., concluding that there is a significant effect when in fact there is not).
2 For more information about statistical software available to calculate d, check www.assess.com.
3 Cohen's textbook (1988) also provides tables with the transformed proportions.
4 Assumes a sample size at remeasure of 50.