Editor's note: Al Fitzgerald is president and founder of Answers Research, Inc., Solana Beach, Calif. Chad Johnson is a statistician with the firm.
In an effort to continually improve a company's product or service offerings while growing a consistent customer base, marketers wisely strive to maximize loyalty and customer satisfaction by deploying loyalty and satisfaction research. Ideally, this type of research will yield the insights needed to achieve a balance between both the amount invested into product development/enhancement and the amount invested in customer maintenance/growth. Unfortunately, while it is imperative to solicit customer feedback to ensure these critical opinions are integrated into product development, it is not as simple a task as merely asking a customer what they like or dislike about a product or service.
Successfully understanding loyalty and satisfaction is a process in which the researcher identifies how overall satisfaction with a company's products and services and loyalty to the brand relate to all specific areas affecting these key issues. Determining this relationship allows researchers to uncover perhaps the most important facet of this kind of study - the drivers of overall loyalty and satisfaction. Gaining a clear understanding of this relationship is most thoroughly achieved using structural equation modeling (SEM). Largely due to its robust modeling capabilities and easy-to-understand graphical output, it is a technique that allows marketers to keep companies informed, and customers contented.
Other methods
Before looking at how SEM approaches the objective of determining the drivers of loyalty and satisfaction, it is a good idea to look at ranking and regression modeling - two of the more common approaches that have been utilized in the past. Ranking modeling is a fairly straightforward and simple method, and regression modeling is a more complicated statistical modeling approach.
- Ranking model
Typically, a customer satisfaction survey includes a series of questions in which respondents rate several attributes of a product or service on a Likert (one-dimensional) scale. This is done twice. First when the respondents rate the attribute's importance in a general context, and then again when respondent rate their satisfaction with attributes in the specific context of the product/service. Because the researcher explicitly asks the respondent for this information, the importance ratings provide what is called "stated importance."
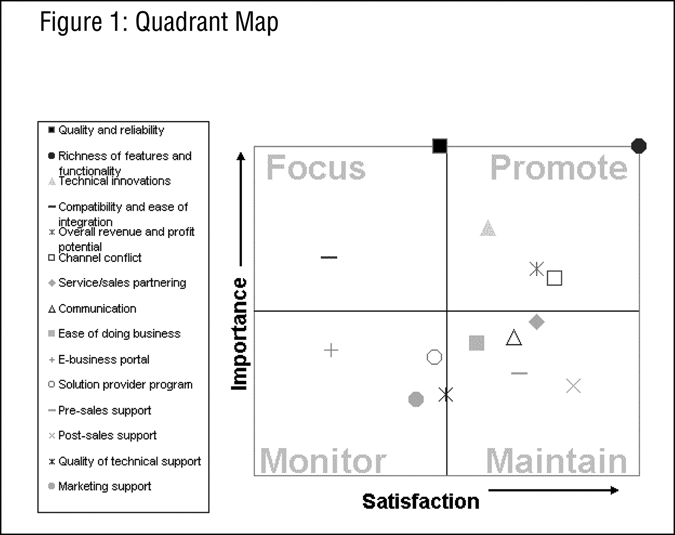
Once the data has been collected, mean scores are calculated for each of the attributes for both importance and satisfaction. The scores are then paired together by attribute and plotted on a scatterplot (Figure 1).
 |
In this way, the key strengths and vulnerabilities are displayed. The x-axis measures importance and the y-axis displays satisfaction. If we divide the plot into quadrants, it provides insight into courses of action that can be taken. Attributes that appear in the upper-right quadrant are items that have both high importance and high satisfaction. These are attributes which should be maintained to hold their current position. Attributes appearing in the upper-left quadrant are items that have high importance but low satisfaction. Customers feel that these are important, but yet they are not being satisfied. These attributes would be considered a high priority to improve customer satisfaction.
Although this approach can provide some useful insight, it has limitations. Ranking models do not take into account the combined effect of all the attributes, but only looks at them individually. Further, they do not incorporate overall loyalty or satisfaction (which is the metric of our focus) into the analysis. Also, this approach utilizes stated importance rather than derived importance, which many researchers prefer.
- Regression analysis
The second approach is to model the relationship between overall loyalty or satisfaction and the causal attributes using multiple regression. The survey questions remain the same as in the ranking model with the exception that the importance rating of the attributes is not needed. In a regression model, overall loyalty or satisfaction is the dependent variable, and the list of causal attributes are the independent variables. The results show how changes in the attributes affect the overall loyalty or satisfaction score. In fact, the model allows us to predict overall loyalty or satisfaction scores using the ratings on the individual attributes. This is a significant improvement on the ranking model.
The regression model addresses many of the limitations of the ranking model. The combined impact of all the attributes is accounted for in the model and all of the attributes are modeled simultaneously. Overall loyalty or satisfaction is incorporated into the analysis. Further, by modeling the data, we have now obtained derived importance scores from the model rather than stated importance. If all of the data is on the same scale, then the coefficients on each attribute can be interpreted as an importance score by dividing each attribute's coefficient by the sum of all the coefficients. The derived importance scores are percentages that add to 100 percent.
Despite these improvements, the regression approach also has criticisms. There are data issues. Regression assumes that the variables in the model are ratio-scale data. Rating data on a Likert scale is close to but not quite at the ratio scale. Regression also assumes the data has a normal distribution. Rarely is that the case with rating data. Also, there can be a problem with the importance scores themselves. If an attribute has a very low true importance, then its estimated importance will be close to zero. Because this is an estimate (and an estimate, no matter how good, has some degree of error) the sign on the attribute may be negative. This is counterintuitive. It implies that as satisfaction with the individual attribute increases, overall satisfaction decreases. This is a very difficult point to sell to management when presenting research results, and often results in distrust of the findings.
Structural equation modeling
Similar to regression, structural equation modeling is a statistical modeling technique that examines the relationships among several variables simultaneously. However, SEM is a much broader analysis that encompasses many specific types of models including regression and factor analysis. SEM models the variance and covariance structure of the data. The data needed for the model is similar to that of a regression.
One of the main advantages that SEM has over regression and other models is that it also includes the ability to handle latent variables in the analysis. Latent variables are intangible concepts such as intelligence, loyalty or satisfaction. Measurement of these types of variables is considered difficult and error-prone because there is no exact measurement scale for these issues. Because these intangible concepts are inherently indefinable, even though we may have collected data on overall satisfaction, this is only an indicator of the true "satisfaction." SEM not only recognizes this, but explicitly measures it as a part of the model in a way that other methods cannot accomplish.
SEM addresses most of the limitations of the other two approaches. Since it is a model, the attributes are analyzed simultaneously, overall loyalty or satisfaction is a component of the model, and derived importance scores like in a regression are estimated. However, SEM is not vulnerable to the data considerations that can affect regression. SEM models the variance-covariance structure of the data which makes it a very robust modeling technique. Having ratio-scale data that is not normally distributed does not adversely impact the results.
We see this all the time. If we print out the rating scores, they tend to be highly skewed toward positive ratings both because respondents are reluctant to give highly negative ratings and because there are typically more satisfied than dissatisfied customers! This is a very significant advantage because it results in more true and valid results. Also, because SEM handles intangible variables such as loyalty and satisfaction and their measurement error into the model, it is a much more thorough analysis of the data and their relationships. In other words, if we really want to understand what is driving brand loyalty or satisfaction with a product or service (Figure 2), we need to a methodology that understands that we are dealing with perceptions and feelings - loyalty and satisfaction. SEM can also handle the fact that many issues that we use to predict satisfaction and loyalty are highly correlated. Further, we are not restricted to a single dependent variable. Multiple variables can be used as indicators of the latent variable "satisfaction" including overall satisfaction and overall loyalty. This allows for the analysis to be extended beyond just satisfaction, but also to loyalty by including variables such as "likelihood to repurchase" and "likelihood to recommend" as indicator variables. Also, the fact that the analysis is graphically oriented is a simple yet powerful advantage. SEM uses path diagrams to graphically depict the relationships of the variables. This makes it very easy to explain the results to clients and management who are often not statistically savvy.
 |
SEM is not a technique without limitations. One disadvantage is that SEM tends to need large sample sizes. Because latent variables and complex relationships among the variables are incorporated into the model, it typically needs more information than other simpler models to calculate estimates. This can add significant cost to a research study. Also, although there are some easy-to-use software packages available, SEM is a complex modeling technique that requires a trained and experienced statistician for deployment.
Understand and identify
Most marketers would agree that understanding what truly drives brand loyalty and customer satisfaction is essential to maintaining a strong customer base. By using structural equation modeling, researchers are able to identify the attributes that predict overall satisfaction or loyalty. By uncovering the key drivers of satisfaction, marketers are in a position to provide products and services addressing the specific needs of their customers.
SEM is able to model the latent variables, key attributes, and satisfaction metrics (e.g., satisfaction, likelihood to repurchase, recommend, and value) simultaneously. Using other modeling techniques, researchers are forced to create many independent models without the capability of seeing how they relate to one another. SEM provides a single comprehensive model of all variables and graphically displays the model in a path diagram that is easy to interpret and communicate to management.