Editor’s note: Gary M. Mullet, an applied statistician, is president of Gary Mullet Associates, Inc., an Atlanta research firm.
As with many other analytical tools, there’s been a recent revival of interest in TURF analysis. While it never completely fell out of use, recent journal articles (see references 1, 3, 4) have demonstrated the benefits of this powerful technique. In what follows, we’ll dredge up the historical roots of TURF, followed by an example on real data. Finally, we’ll discuss some extensions and warnings.
History
The consensus of several colleagues and myself is that total unduplicated reach and frequency (TURF) analysis was introduced to the research community in the early-to-mid-1970s via an article in the Journal of Advertising Research. The exact date and title of the paper are lost in the recesses of our collective failing memories. (If any of y’all could provide the exact citation we’d be grateful.) A major purpose of TURF was to provide purchasers of magazine advertising a more cost-effective method of allocating scarce funds.
As conceived, TURF had both the reach and frequency components built-in. We shall see subsequently that modern research practices generally separate these two pieces of the total picture. In oversimplified form, the early versions of the technique would ask respondents to examine a list of magazines and then place a check mark next to those that they regularly read at least three out of any given four issues, say. This comprised the unvarying frequency portion of TURF - that is, frequency was always three out of four issues.
The value of the originally conceived TURF can perhaps be seen in the following (over)simplified example. Let’s assume that a manufacturer of kitchen sinks and faucets is trying to decide where to place ads for a new line of products. The choices are limited to only three and the costs for a full page in each are about equal. So a data collection agency is contracted to determine which of the three potential vehicles are read (at least three out of four issues) by how many respondents. After 1,000 interviews with members of the target audience are completed, the following data summary is given:
Good Homekeeping (A) 60%
House and Grounds (B) 50%
Kitchen Expressions (C) 30%
A few things are readily apparent. First, placing an ad in each of A and B will not deliver 110 percent of the audience - there must be some overlap or duplication in readership. In fact, depending on the degree of duplication, an ad in A and another in B will deliver between 60 percent and 100 percent of those in the target market (we’re neglecting the issue of sampling error until later). Likewise, ads in both A and C will deliver between 60 percent and 90 percent of the audience and, finally, using both B and C will give us between 50 percent and 80 percent. Without further information about the degree of joint readership we cannot come up with the optimal media plan (those of you who are fortunate or, maybe, unfortunate enough to recall the term “Venn diagram” will know what’s needed here). And that’s what a TURF analysis computer program does - counts the unduplicated audience for all pairs, in our simple case, of magazines. Unduplicated readership is expressed in the number or percentage of our respondents who read A or B or both, and so on for each other pair of magazines.
No big deal for selecting two out of three magazines but what if the task was to select the best four out of 10, say? Then we would have 210 possible sets of four to examine and I promise that if you tried to make a list of all 210 combinations of four letters from the letters A-J you would not have a fun time. And performing an ad hoc tabulation of the combinations would drive you even further up the wall. That’s why back in the dark ages of computing, where the computer was fed information on punched cards (frequently and erroneously called IBM cards), the inception of TURF analysis programs was a major contribution to marketing and advertising research.
Reach
Today everyone has ready access to a desktop or laptop computer with lots of ROM and RAM and a high clockspeed. So within reason - about which more later - it’s quite a simple task to separate the reach component from the frequency component of TURF. I’m sure that a while huge majority of TURF studies conducted by contemporary marketing researchers look at each of the two parts separately, there are certainly more than a handful that do reach and reach only. The following table shows the results of an actual study, although disguised somewhat for proprietary reasons.
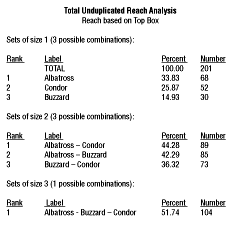
Respondents were asked, on a traditional five-point scale, purchase intent for each of three (we sometimes do only a few concepts in spite of the capability to do many, many more) concepts. The actual printout from a TURF (REACH) computer program follows.
 |
For each set or combination of items, we get an identifying label, the percentage of respondents reached by the combination (based on our total sample size) and the actual number so reached. Notice a couple of things that the program also does. First, it tells you the total possible number of combinations of the given size. No big deal with only three items, but it’s a nice addition for, say, the number of combinations of 13 items out of 25 possible (5,200,300). The program then sorts the combinations from high-to-low in terms of reach. Again, not a big deal for three concepts but a big, big deal for the 5,200,300 noted above. You have the information to calculate that 31 respondents were very favorable to both Albatross and Condor, although I can’t imagine why you’d want to for most projects.
The proprietary reach program that I use gives a couple of other nice options. First, you don’t have to print all of the combinations. You can limit your output to the top 20 or 25 or . . . combinations (plus ties, which are given automatically) - your choice. Again, no biggie, but a good way to save a few trees when you start printing output from a more substantial analysis. Another feature is that you can specify the maximum number of combinations or subsets that you want to consider. If, for instance, you are doing a TURF analysis for a potential line extension and you have, say, 25 possible items that could be added, there’s no sense calculating and printing anything above four items if that’s the most that will ever be added. (These two options also are in operation on the frequency program that I use, and so won’t be mentioned again below.)
Frequency
Step two in the total TURF analysis is to compute the stated purchase frequencies for various combinations of the same concepts. Generally, these are based only on those who gave the criterion answer to the question we use for reach. In our case this is top box on the five-point PI scale. In the case in hand, the item is low-priced and multiple purchases within and between products is possible. The question was originally phrased to reflect purchase behavior within a particular time period, e.g., one month, one week, etc. The frequency portion of the output looks as follows:
 |
The left side of the table gives the same information as we saw in reach: the rank and the combination label. We have some new information as well. “Number” indicates the number of respondents (out of 201) who gave a top box score and a non-zero purchase frequency. This column will always be less than or equal to the corresponding numbers in the reach table for the following reason. As anyone who has been in marketing research for more than a week or so can attest, there are almost always respondents who will tell you that they really like your concept(s) but that they will not ever purchase any. So, too, in our case.
The second column is nothing more than the total number of purchases, summed across all of these respondents who had earlier given a top box answer. The next two numbers are means - the first (“Subset”) comes from dividing the total score by the entry in the number column. The second is based on total sample; here n=201. We use the subset mean to examine the output for products that appeal to a relatively few respondents, but may be purchased relatively often (or in larger quantities) by those very respondents. Buzzard is such a concept. Only 30 respondents gave it a top box score but those 30, on average, say they will buy a lot more of it than those who like either of the other two concepts (note that there is some overlap, as determined by the previous reach analysis).
As with reach, we can now determine which combinations of two or three or . . . will be purchased with the highest frequency, on average. In other words, when we get to combinations of two or above, the total score consists of the sum of all items in a given combination. These will rarely be individually equal. In addition to the options mentioned above for the reach program, the frequency algorithm allows the user to sort the data by either the total mean (as was done above) or the subset mean. Note that we have now separated reach and frequency, which the earliest TURF analyses did not do.
Some variations and caveats
Let’s start with some “be carefuls.” If you give purchasers in a given category, say soft drinks, a series of concept statements to evaluate, chances are pretty good that they will be positive to many, if not most. When we then ask the frequency question, even if we limit it to those which evoke a positive response originally, many will answer with big answers to most concepts. It might be better to constrain their frequency response to their actual behavior. That is, if someone buys, say, a case of soft drinks each week, have them allocate a month’s purchases over both the major existing brands and the concepts. Otherwise, the concepts are probably going to show larger sales in the TURF analysis than will actually occur. Some researchers allow for this by including both existing products and concepts in the entire data collection process and analysis, for both reach and frequency.
Don’t overwhelm either the respondent or your analyst. Having people evaluate, for example, 60 items, especially in a low-to-moderate interest product category, will most likely yield data which aren’t going to be helpful at all. Additionally, 60 items puts a tremendous strain on the analytical program. If, for example, you want to select 15 items from 60 that have the greatest reach, your computer will have to evaluate 5.32 x 1013 possibilities, keep them in memory and sort them. Probably better to keep the task smaller for everyone concerned.
It’s not unusual, especially in reach analysis, to have several sets of combinations of a given size with equal or near equal appeal at the top of the list. For example, Conklin, et al 2, list the reach of all 10 possible combinations of three items from six potential concepts. The top three all reach 119 respondents, the next two appeal to 118, then we see 117, 115, 114, 113 and 111, respectively, for the final five combinations. While we doubt that any analysts would seriously propose that any of the three tied combinations are substantively better to offer the public than either of the next two, this is not an atypical situation and has occurred quite often in studies we’ve been involved with. If possible, the researcher should next perform the frequency analysis to help clarify the issues. In fact, when frequency is considered, it’s not out of the question for the last place combination from reach to move up to first place, especially if the reach number is as close to the top as that above. Another tiebreaker is to consider the profit/cost variable, as noted below.
For the more statistically-minded, it’s a relatively easy task to carefully run significance tests on the results of either reach or frequency. Remember that the tests are to be either on nominal or metric dependent (repeated measures) data and, then, with careful bookkeeping you can decide which of the top reach or frequency numbers are significantly different from which others. You can also determine whether, say, the top combination of three items is significantly different from the best one of four items, in terms of either reach or frequency. Again, this is somewhat painstaking but may yield very positive results.
Now on to some extensions. Since reach and frequency are now analyzed separately, we have added great flexibility to the total package of TURF analysis. For instance, we can easily include selling price, net profit or other financial data when setting up and then running the frequency analysis. We are then going to be looking for combinations that maximize, say, total dollar sales or total profit. We could also look at production time, particular raw materials consumed and so on and so on. It’s an easy matter to weight the stated number of purchase by any relevant quantity.
In summary, successful use of either or both parts of TURF analysis, while not a panacea, is limited only by your own ingenuity.
References and readings
1. Cohen, E. (1993), “TURF Analysis,” Quirk’s Marketing Research Review, VII (June/July), 10-13.
2. Conklin, M. and S. Lipovetsky (1999/2000), “A Winning Tool for CPG,” Marketing Research, (Winter/Spring), 23-29.
3. Miaoulis, G., V. Free & H. Parsons (1990), “TURF: A New Planning Approach For Product Line Extensions,” Marketing Research, II (March), 28-40.
4. Mullet, G. (1997), “TURP: Total Unduplicated Reach and Profit,” Canadian Journal of Marketing Research, 16, 95-100.