Editor's note: Joseph. L. Kreitzer is president and CEO of Loon Valley Software, Inc. and author of ForeProfit, a forecasting and linear programming package. He has a Ph.D. in economics from the University of Iowa and he is currently an associate professor at the College of St. Thomas, St. Paul, Minnesota.
Regression. The very word glazes the eyes of capable researchers. It fills their minds with thoughts of their former selves and conjures dark, Freudian images among those with psychology backgrounds.
The reality of regression analysis, however, is that it provides a tool offering all of the analysis potential of ANOVA (Analysis of Variance), but with the added ability of answering important questions ANOVA is ill-equipped to address.
If regression isn't a Freudian term, then just what is it?
There are many statistical techniques for determining the relevance of one measure, e.g. purchases, to another, e.g. price. The strongest of these techniques are analysis of variance, goodness of fit (GOF) (e.g. cross-tabulations), and regression analysis. Each is capable of answering the same basic question of whether or not variation in one measure can be statistically related to variation in one or more other measures. Only regression analysis, however, can specify just how the two measures are related. That is, only regression can provide quantitative as well as qualitative information about the relationship.
For example, suppose that you need to address the question of whether or not sales (in numbers of units sold) can be related to your price. Suppose further that you use ANOVA and find a statistically significant relationship does exist. That's it. You've gone as far as ANOVA can take you.
Regression analysis offers additional information which neither ANOVA nor GOF can provide. Specifically, regression analysis can tell you how much an additional dollar (i.e. change in price) can be expected to change sales. This information provides an objective basis for the infamous "what if" problems so central to Lotus-type simulations.
A second advantage of regression analysis is its ready application to graphic imagery. Regression is sometimes referred to as "curve" or "line" fitting. The regression output, indeed, yields an equation for a line which can be plotted. The old adage about "a picture is worth a thousand words" holds especially true for regression lines. The image of actual data plotted against predicted values is instantly accessible to even the staunchest statistical cynic. A regression which has been well-specified provides its own pictorial justification.
In the beginning there are numbers
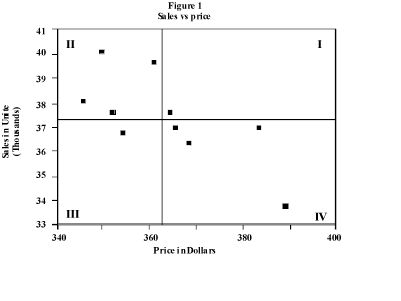
Suppose that you have measured the numbers of units sold in various weeks and kept track of the price you had charged during the same weeks. Table 1 contains some hypothetical pairs of sales and prices. A scatter plot, depicted in Figure 1, provides some immediate sense of the relationship between the two measures.
 |
Table 1
Hypothetical Sales and Prices
| Week | Sales (Units) | Price |
| 1 | 33,800 | 389 |
| 2 | 37,000 | 383 |
| 3 | 36,300 | 368 |
| 4 | 39,700 | 361 |
| 5 | 36,800 | 354 |
| 6 | 37,600 | 352 |
| 7 | 37,600 | 364 |
| 8 | 37,000 | 365 |
| 9 | 38,100 | 346 |
| 10 | 40,100 | 350 |
Both correlation analysis and regression analysis work from the respective average values of the two measures. In effect, they attempt to determine if systematic deviation exists of one measure from its mean to corresponding deviations of the other measure from its mean. The dotted lines which note the location of the respective mean values split the scatter diagram into four quadrants, labeled I, II, III, IV.
In our example, we would like to know if above average sales could be systematically related to less than average prices (and therefore less than average sales could be related to above average prices). If this situation exists, then the preponderance of points in our scatter diagram should lie in quadrants II and IV.
If we demonstrate that this relationship exists, we can evaluate the wisdom of decreasing the price as a tool for increasing sales. This scenario is illustrated in Figure 1. If no systematic deviation can be shown, then one could not count on any predictable response in sales to variations in the price. Essentially, the numbers of sales would be unpredictable (by price). Knowledge of the price in relation to average price would not cause you to change your projected numbers of sales from the average of all past weeks. This case is illustrated in Figure 2.
 |
In the former case, a line drawn through the points would have a negative slope, i.e. an increase in pace would be associated with a decrease in sales. The line forms the basis for projecting likely sales for any price. In the latter case the best fitting line would be a horizontal line, i.e. a line with a slope of zero.
(This case does occur, by the way. In one instance a firm's price had no statistically significant impact on their sales. The reason, as it turned out, is that the firm was a price "follower" who adjusted price in relation to the industry leader. The significant price turned out to be the competitor's, not their own.)
In the middle there is methodology
I remember my introduction to regression. After carefully plotting points on a scatter diagram, we were instructed by the prof to take out a ruler and place it across the diagram in what we considered to be the best location. After sketching in our "fitted" lines we were to come up with the equation of the line we had drawn in, which was simple enough, although altogether subjective.
After everyone reported their variants of the same equation, we learned the unambiguous technique of least squares. Least squares is a mathematical solution to the problem of finding the "best" line. It does so by finding the equation of the line which has the least residual (remaining) variation of actual values from the fitted line. Any other line you draw in will have a larger typical error.
In addition to its unambiguous solutions, the least squares method is able to incorporate more than just one explanatory variable and has known statistical properties. Without the knowledge of statistical properties one could not definitively note dependence of one measure on another measure. The inability to do the former yields an inappropriately naive view of the world.
In the end there will be more numbers
Fortunately, knowledge of the mechanics of the regression algorithms are unnecessary for successful application and interpretation of a regression line. Regress, if you will, to sixth grade math, when you learned the intricacies of graphing lines. A simple line consists of two parts. The intercept of a line gives the value of a dependent measure, sales, when the independent measure, price, has the value zero.
In our example, the intercept would provide the number of sales which are likely to occur when the product was given away free. Notice the apparent silliness of this interpretation. Don't fret about it, however, as this intercept should not be literally interpreted this way. It is necessary for the statistical interpretation to have an intercept. The regression algorithm would tell us that this number is 69,438.
The second part of the line is the interesting one. It shows how to transform one measure into the first by means of a "slope." The slope gives the change in the dependent measure for a one unit change in the independent measure. In our example, it shows the additional sales related to the change in price of one unit, e.g. $ 1 . The regression-supplied estimate of this number is -88. (The package I used reported this number to be -88.2120, but for clarity of illustration we needn't bother with all of the extra digits. The same is true of the intercept reported above.)
The regression would then take on the form:
Q = 69,438 - 88 P
where: Q is sales in units P is price in dollars
If you wanted to know the likely number of sales when the price is set at 300, you would solve the equation:
Q = 69,438 - (88 * 300) = 69,438 - 26,400 = 43,038
Similarly, sales at a price of 350 would likely be:
Q = 69,438 - (88 * 350) = 69,438 - 30,800 = 38,638
How much will a $1 change (which implies a positive change, or increase) in price affect sales? Simply read the slope coefficient. A $1 change in price will decrease sales by 88 units. A $10 change in price will decrease sales by 880 units. A $5 decrease in price will increase sales by 440 units.
Finally, there is reality
It would be a rare day in the real world when variation in a measure could be explained solely by variation in only one other measure. In our example we might well expect, and find, that our advertising and our competitors' prices influence sales of our product. Regression analysis can incorporate these new measures in the same manner as our price.
Each new explanatory measure is equipped with its own, unique slope which transforms the variations of the new measure into variations of the dependent measure. The interpretation and arithmetic for each additional measure are as above.
Suppose that we included information about our advertising when estimating our regression line. The comparable advertising figures, for example, numbers of column inches published per week, are listed in Table 2. It seems only reasonable that the more we advertise, the higher the likely number of sales. The regression algorithm reports this number to be 145. This means that one additional column inch of ad space increases sales by 145 units.
Table 2
Hypothetical Advertising Amounts
| Week | Advertising |
| 1 | 995 |
| 2 | 1010 |
| 3 | 995 |
| 4 | 998 |
| 5 | 982 |
| 6 | 981 |
| 7 | 992 |
| 8 | 992 |
| 9 | 976 |
| 10 | 978 |
Since our advertising now can explain part of the sales variations, the role of price in sales can become clearer. We see this in a different coefficient for the price variable, - 178, as well as a different intercept, -41,794.
The revised regression now looks like:
Q = -41,794 - 178 P + 145 A
where: A is our advertising space in column inches
If we charged a price of $350 and purchased 1000 column inches of advertising then our likely sales could be estimated as:
Q = 41,794 - (178 * 350) + (145 * 1000) = -41,794 - 62,300 + 145,000 = 40,906
The slope coefficients are interpreted in the same way as above, with one important warning. The coefficients yield the expected change in the dependent measure for a one unit change in each respective independent measure, assuming that the other independent measure(s) do not change in value. Specifically, a one dollar change in the price will likely decrease sales by 178 units, assuming no change in advertising. Similarly, a one unit change in advertising will increase sales by 145 units, assuming price remains constant.
If both price and advertising are to be changed then the effects are simply added together. If price is to be reduced by 5 (i.e. changed by -5) and advertising increased by 2, then the net change in sales would be given by:
Change in Q = - (178 * -5) + (145 * 2) = 890 + 290 = 1180
Adding additional information, such as competitors' prices and advertising, causes similar modifications in the equation and its interpretation.
Evaluating a regression's fit
Anyone can draw a line through a set of points. But clearly a (straight) line drawn through a circle does not describe the circle. One must be able to evaluate the reasonableness of a regression to use it wisely. Effective use of regression is clearly an acquired skill, but even a novice should be able to make some preliminary judgments regarding a regression's fit. There are basically three diagnostic processes in evaluating a regression: comparing coefficients' signs, determining significance of each variable, and evaluating the overall fit.
Signs. The first step in evaluating a regression is to consider the signs of the parameters. If you have reason to believe two measures are positively correlated then the regression coefficient should be positive. If a negative coefficient showed up then you basically have two conclusions: you were wrong in expecting the positive correlation or your regression equation is misspecified, i.e. contains redundancies or inadequate information. Misspecification is a serious problem, and is discussed in greater detail below.
If the regression coefficients have the expected sign, as ours do, then you have some assurance that you have chosen the "correct" set of independent measures. The next question to address is whether or not those coefficients are meaningful. The problem is that we have only sampled the relationship between sales, price, and advertising. As is true with any sample, the observed value needn't, and in all probability won't, coincide with the "true" value.
Significance. One coefficient value, in particular, is of great concern. If the true coefficient value is zero then the two measures are not related. (Their correlation coefficient would be zero and the partial F statistics insignificant.) Even if the two are unrelated, unfortunately, a sample coefficient would not likely be zero. In most cases a Student's t test is employed to determine the significance of the coefficient. If sufficient numbers of observations are available then a normal distribution can be used.
In our case, the estimated t values for the price and advertising measures are - 4.06 and 2.48, respectively. The regression has 7 degrees of freedom (10 observations minus three estimated coefficients). Using a .05 level of significance, the critical t value is 2.36. Since both estimated t values exceed the critical value we can conclude that the measures are significant in explaining variation in sales. (If you used ANOVA to test for a relationship you would obtain significant F values for both measures.)
Note that the magnitude of the coefficient isn't sufficient information to determine significance. Large coefficients might not be "large enough" to be significantly different from zero while some very small coefficients might be more than "large enough" for significance.
Fit. One could have a regression for which the signs were correct and the coefficients significantly different from zero, but which has little practical value.
The most intuitive explanation of overall fit is the "coefficient of determination" most commonly called R2, or "R squared." It reports the percentage of the total variation of the dependent measure which is explained by the regression equation. The number ranges from 0 to 1, where one hopes for larger values. A regression with an R2 of .1 is not very complete, casting doubts on the accuracy of the estimated coefficients. An R2 approaching 1 suggests that the regression's independent measures can explain virtually all of the variations of the dependent measure.
A mathematical quirk allows this R2 measure to increase as more independent measures are added. To counteract this inflationary tendency a second R2 called the "adjusted R2" is calculated which handicaps the R2 by the number of independent measures used in the regression. It is interpreted the same way as the R2, and is considered the more accurate of the two statistics.
In our case these numbers are 72.9 and 65.2, respectively. The regression can be said to explain 65.2 percent of the variation in sales. Is 65.2 percent "enough" to justify the technique? Fortunately there is a statistical test, you ANOVA users have been thinking about for several paragraphs, which can answer this question. The R2 statistic is simply a variant of the F statistic. Indeed the F statistics generated by an ANOVA routine and by a regression routine are identical. If the F statistic is significant, then the explained variation is significantly greater than that left unexplained. In our case the F statistic is 9.45, greater than the critical value of 4.74.
One additional statistic generated by a regression is the standard error of the regression. It is a measure of the residual variance. In our example the remaining variance is 1039, representing an average percentage error of only 1.7 percent.
Figure 3 shows the actual and fitted values for each of the 10 weeks, using both price and advertising to explain variations in the sales volume.
 |
If only it were this simple
There are pitfalls in regression analysis that can undermine the veracity of the entire estimated equation. Basically there are two categories of problems, only one of which typically poses major problems for the researcher.
The more benign types of problems generally lead to inflated error terms- therefore decreased accuracy. They do not, fortunately, lead to biased estimates. There are problems in reliably interpreting individual coefficients in these cases but not for using the equation as a whole. These problems are:
Multicollinearity. The independent measures are, themselves, closely correlated. This causes confusion in determining the importance of any single measure. For example, if one firm "followed" the pricing of a competitor then inclusion of both prices would be redundant.
Autocorrelation. The error terms are related sequentially. This type of problem is common in time series data, where sales might fluctuate around some long-term growth path. Much like the concept of a business cycle, you might find the regression consistently over-estimating values for sequential periods, only to begin a pattern of underestimation.
Heteroscedasticity. This problem arises when a regression fits "better" for some values of an independent measure than for other values. An example would be an equation for sales, which seems to compound over time. By virtue of its compounding, the equation will generate smaller absolute errors early in the series rather than later, when the magnitudes of the measure are much larger.
At this point it is worth noting simply that techniques have evolved which neutralize many of the effects these complications generate. Failure to deal with these problems yields greater uncertainty than is necessary, but does not, in general, tend to seriously mislead the analyst.
By contrast, specification. errors are serious. Failure to deal with these problems can cause major difficulties. There are three major types of misspecification.
Failure to include relevant information, omitted variables, forces the regression to allocate explanatory power among too few independent measures. It is much like trying to explain sales only by using price, as we did originally. Notice the difference in coefficients in the two equations. When price was forced to explain "everything," the coefficient was only - 88 compared to -178 when part of the explanatory burden was assumed by the advertising measure.
High R2 statistics suggest the regression does include most of the relevant information. Lower R2 values, 65 % in our example, suggest, but do not conclusively show, there are other relevant measures which have not been included. Were we to include additional relevant measures the regression coefficients would take on still different values.
Failure to include related information, omitted equations, has a similar effect on the coefficients. Suppose that the amount of advertising was at leas/partially determined by the level of sales, e.g. a scheme which set the advertising budget as some base figure plus 10 % of the sales level. This is, in effect, a second equation that is clearly related to our sales equation. Advertising is dependent on, not independent of, sales and therefore our sales regression will give biased estimates of our coefficients.
Incorrect form of the equation is the last misspecification type. Regression only works for "straight" lines, but the real world is rarely linear. In many cases the straight line approximation of regression is entirely satisfactory. In others, e.g. learning curves or product life cycles, a linear relationship is altogether unrealistic.
Without going into detail, suffice it to say, again, that techniques exist to mitigate the effects of these problems. The remedies are generally easy to employ, but the initial detection of the problem is less obvious.
So why would anyone not use regression analysis?
There are basically two reasons why regression analysis might not be the first choice of technique for a researcher.
Regression analysis assumes, indeed requires, the error terms to be normally distributed. The normality requirement is sometimes more than a researcher is willing to take on. Non-parametric techniques, which do not make such a restrictive assumption, are better suited to the temperament of these individuals. In general, however, the normality assumption is not outrageous if a sufficiently large sample can be obtained.
The second reason regression might be avoided is paradoxically related to regression's strong suit-quantification of relationships. In some cases one might wish to determine whether or not two measures are significantly related, yet it doesn't make immediate sense to quantify the relationship between qualitative measures, e.g. gender and location preference. More advanced regression techniques exist (LOGIT, PROBIT, Discriminant Analysis) which can be useful in analyzing qualitative models, but discussion of their characteristics is beyond this article. Basically they convert qualitative problems into one of probability estimation, e.g. finding the probability that a male would choose to locate in area X.
A variant of this concern is that regression equations will be inappropriately interpreted and/or glorified. Given the number of potential pitfalls, any regression should be considered suspect until carefully scrutinized. There is a tendency on the part of some decision makers to give undue credence to any tool which has numbers associated with it. Should your audience consist of individuals with this affliction then you may be well advised to introduce regression analysis slowly and only in conjunction with education about regression's uses and misuses.
Where might you go from here?
There are a number of excellent texts on regression analysis and almost every major statistical package offers a regression routine or two. Economists, who have played a disproportionate role in the development of regression tools, fondly and conceitedly talk of econometrics. You might look for other texts using this term in their titles.
Here are some of my favorites:
"Using Econometrics: A Practical Guide." A.H. Studenmund and H.J. Cassidy. Little Brown and Company (Boston, 1987). One of the more accessible, mildly rigorous works, it includes several "cookbook" features which help beginners evaluate their regressions.
"The Application of Regression Analysis." D.R. Wittink. Allyn and Bacon (Boston, 1988). This is written at a fairly low level of rigor. It doesn't cover many of the remedies alluded to above, but for a complete novice it might be a good introduction. If you go this route, please follow it up with one of the other texts.
"Forecasting: Methods and Applications, 2nd ea." S. Makridakis, S.C. Wheelwright and V.E. McGee. John Wiley and Sons (New York, 1983). The book is written, obviously, with forecasting in mind. It is somewhere between the two previous works in rigor. About 1/4 of the book is devoted to regression analysis. The remainder of the book deals with other forecasting techniques, both quantitative and qualitative. It is a classic worth acquiring.
"Econometric Statistics and Econometrics, 2nd. ea." T.W. Mirer. Macmillian Publishing Co. (New York, 1988). Written at a mildly rigorous level, it is fairly accessible, has many examples and discusses remedies for the problems noted above.
For those with strong hearts and mathematical statistics backgrounds, there are several very good texts. Many are cited in the works noted above, and I would be happy to provide any reader with some suggestions.