Editor's note: Steven J. Fuller is president of InforMedix Marketing Research, Inc., Highland Park, Ill.

Stratified random sampling is a technique used to improve the accuracy of survey results or to lower the cost of a survey without losing accuracy. With a properly designed sample, the total number of survey contacts can sometimes be reduced by more than 50 percent, compared to simpler plans, without losing any accuracy in the results. The technique is often used in preparing random samples for large quantitative surveys.

Stratified random sampling involves dividing the market up into segments that are different from each other, studying each of the segments separately, then putting the separate results back together using a weighted average. This weighted average of several precise measurements can be better than a general measurement of the whole diverse market.

To gain the greatest benefit from this technique, it is important to have some advance information about the market being surveyed. In particular, one must recognize that the total market contains subsets that are different from each other - and be able to say how the subsets differ. It is common to subdivide U.S. markets into groups that differ by geography, volume of purchasing, age, sex and so on.

This report explains the benefits of stratified random sampling, and demonstrates how to construct such a sample, using real data. The example comes from a research investigation of the market for patient monitors in U.S. hospitals, but the techniques can be applied to almost any product or customer group.

The easy way - proportional sampling

To understand the method of preparing a stratified random sample, and the benefits this technique can provide, it is helpful to start by describing an easier and more common method used for selecting a sample. Very often, samples are chosen with a simple technique called "proportional sample allocation," which is no more than picking survey respondents at random from the complete list of available respondents, called the "universe" of respondents.

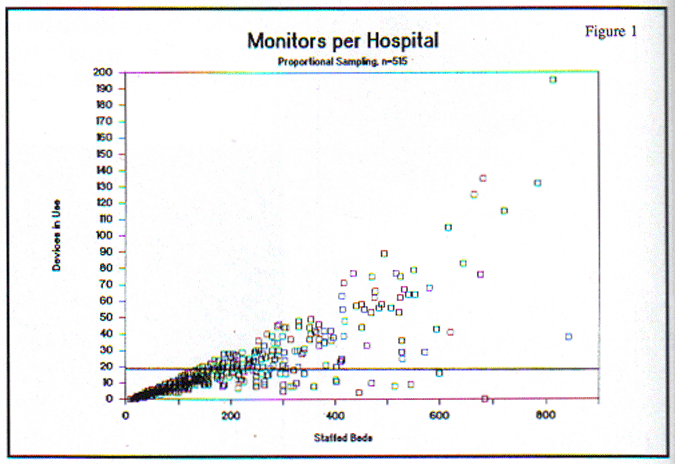
For instance, if we want to know what fraction of the hospitals in the country use a particular type of high-tech patient monitor, we can just survey, say, 10 percent of all the hospitals in the AHA Guide, or another complete list of hospitals. In this case, the sampling proportion is 10 percent, and if the universe contains 5,151 hospitals, we would survey every tenth one in the list, until 515 sites had been interviewed. The results of the survey would give a fairly accurate estimate of the average number of monitors per hospital, and the total number of monitors in the U.S.

The results of such a survey are shown in the graph in Fig. 1, and the horizontal line points out the average number of monitors per hospital, which is about 20.

Wasted telephone calls

While this is a useful result, the question remains whether it was acquired in the most economical way. Many research analysts would look at the graph in Fig. 1, and wonder what they really learned from all the data points forming the dense black cloud in the lower left corner. And they might be uncomfortable with the small amount of solid information they have about larger hospitals, where the data points are few and sparsely distributed.

There are two reasons why this sampling plan wastes the researcher's time and adds unnecessary charges to the telephone bill or the business reply mail account. One is that it may not match a company's marketing priorities; the other is that a good deal of the information collected is statistically useless. These problems, and ways to solve them, are explained below.

The marketing problem

The problem from a marketing perspective is that most manufacturers of medical products are more interested in large hospitals, which drive the majority of their sales and product development initiatives. So any survey that contacts many small hospitals at the expense of sampling the large ones will be questioned by the sales manager, if not the company's statistician. The proportional allocation which gave the data in the graph is presented in Fig. 2.

It is easy to see that small hospitals accounted for a very large part of this survey: 217 respondents, or over 40 percent of the total, were hospitals under 100 beds. This is because 40 percent of the hospitals in the U.S. are under 100 beds, and the proportional allocation scheme required surveying 10 percent of hospitals of all sizes. But unless the company has a particular product strategy aimed at small hospitals, it would be an error to focus so much of the survey on small customers.

Ten percent of the large hospitals were contacted, too. But since there are relatively few large hospitals, only 98 responses were gathered from sites with more than 300 beds. This means that less than 20 percent of the survey provided information about a market segment that is usually of great importance to medical market researchers.

From a marketing standpoint, it may be acceptable to arbitrarily eliminate some parts of the hospital market altogether. Many survey planners do this by excluding hospitals under 100 beds, long-term care hospitals, psychiatric hospitals, Veterans Administration sites and so on. Others decide from the outset to survey only 1 percent of the smallest hospitals, while developing a properly stratified sample for the rest. There is nothing wrong with these solutions, as long as the researcher is willing to settle for less accurate information about the under-sampled parts of the market.

The statistical problem

The second concern is statistical, and should be kept in mind when planning any market research survey: When you have enough information to draw conclusions with confidence, it is time to stop collecting data. In the example, it is clear that small hospitals don't vary widely in their use of monitors. After this became evident (probably after a few dozen interviews), nothing useful was gained by continuing the survey to hundreds of small hospitals.

With survey results such as those in Fig. 1, the researcher can be extremely confident in drawing conclusions about hospitals under 200 beds. Among larger hospitals, though, especially those over 400 beds, it is anyone's guess what the average number of monitors per hospital might be. This is because large hospitals vary greatly in their use of this product, and the survey has not gathered enough information to state any conclusions with confidence. To demonstrate this statistically, the chart in Fig. 3 shows 90 percent confidence intervals for market estimates in each size segment.

It is obvious that a proportional sampling plan has yielded little variation among small hospitals, and quite a lot of variation among large ones. (The smallest bed-size category, hospitals with 1-24 beds, also contains a large statistical variation. This is because all of the hospitals had either no monitors or a single device, giving an average which is not close to either of the data points. However, this finding was considered to be sufficient information about the smallest hospital group, and the segment was eliminated from any further survey work.)

The most important result is that the overall accuracy is no better than plus or minus 5.33 percent (for a 90 percent confidence interval). Narrowing this wide range is a central goal of stratified random sampling.
Incidentally, it is quite common to find results like this within the hospital market - there is nothing unique, statistically, about the market for patient monitors. In many ways, small hospitals are alike, while large hospitals differ in their buying patterns and use of products. Some factors that can cause large hospitals to be so diverse are their efforts to specialize in particular areas of medical care, participation in multiple group purchasing contracts, and widely varying economic conditions encountered by urban hospitals.

Stratification

Optimal Allocation using a stratified random sample solves the statistical problem found with proportional allocation, by ensuring that enough respondents are surveyed in each segment to provide the greatest possible level of accuracy for the overall results.

The key lies in being able to identify subsets of the market where answers vary widely, and others where answers are essentially the same. It is very common to subdivide hospital markets by bed-size, but only a little more effort is required to segment by geography as well. Many surveys of hospitals use two- or three-dimensional stratification schemes, resulting in dozens of market segments. To keep the explanations simple, the example used here segments the hospital market only by bed-size.

Planning the stratified sample

In the example, the number of patient monitors in small hospitals is small, and does not vary greatly from one site to another. Optimal Allocation takes advantage of this observation by specifying a low number of survey contacts within this market segment. On the other hand, large hospitals often use many monitors, but the data points can be "all over the map." Optimal Allocation solves this problem by indicating that more survey responses should be found in this segment.

Statistical textbooks provide formulas to determine just how large the sample should be in each market segment, to maximize accuracy and narrow the confidence intervals. These formulas state that allocation of the sample to each segment should be proportional to the segment's standard deviation multiplied by the number of potential respondents in the segment.

The results of these calculations are shown in Fig. 4. For each bed-size category, the number of hospitals in the U.S. has been multiplied by the standard deviation of the number of monitors measured in the first survey. The seven results show the proper weight to be applied to each segment in selecting a number of respondents. (As mentioned earlier, the smallest category was eliminated after the initial survey.)

To To prepare for a second survey of the monitors market, a new stratified random sample was designed. The total number of respondents was kept at 515, but these were re-allocated according to the fractions given in the column on the right in Fig. 4. The difference between Proportional Allocation and Optimal Allocation can be seen by comparing Fig. 5 and 2.

Improved results Using the new stratified sample, the survey was conducted again, and the results are shown graphically in Figure 6.


The benefits of Optimal Allocation of the sample are seen by comparing Fig. 7 with Fig. 3. Two changes have resulted from stratified random sampling. First, confidence intervals are now tighter in large hospital segments, where the number of monitors is larger and less predictable from one hospital to another. Second, the overall average for the total market can be predicted with much better accuracy: the 90 percent confidence interval has been narrowed from more than +/- 5 percent with Proportional Sample Allocation, to less than +/-3 percent with the Optimal Allocation.

Smaller surveys or better accuracy - you can choose

Armed with information about individual market segments and the variation of responses to this type of survey, a market researcher can design a stratified random sample that meets the particular budget or accuracy objectives required for the next survey.

Obviously, with an unlimited budget, it would be possible to achieve the greatest possible statistical accuracy by surveying the entire available universe of respondents. In the real world, we are usually faced with a fixed budget, which means a limited number of completed interviews.

When budgets are limited, the techniques of stratified random sampling allow the analyst to distribute the sample across various market segments in a way that maximizes the accuracy of the results. For instance, in the patient monitors survey, the researchers found that a stratified sample of only 225 hospitals would have provided about the same overall accuracy as the original 10 percent proportional random sample. In other words, preparing a stratified random sample could save the client company the cost of 290 interviews - more than half of the data collection cost!

Once a researcher is familiar with the methods used, some simple spreadsheets or database calculations can make it easy to calculate the required sample size. And usually, it is well worth the effort, since computerized calculations are not expensive, but unnecessarily large research surveys are.

It is also possible to use these statistics to determine what sample size would be needed to give a desired level of accuracy in the results. If the researcher needs to be able to claim "+/-2 percent accuracy with a confidence level of 90 percent", a large sample size will be dictated. If "+/-7 percent with a 90 percent confidence level" is satisfactory, then a smaller sample will do.
Fig. 8 shows how many responses would be needed in order to arrive at 90 percent confidence intervals of various sizes, for the patient monitor survey used in the example.

What about first-time surveys?

Stratified random sampling techniques can be applied fairly easily, but they do require advance measurements of each segment of the market to be surveyed. In the example presented here, the required Optimal Allocation of the sample could be calculated only after the first survey had measured the standard deviation of the number of monitors within each hospital bed-size segment. If an earlier survey can be used to determine the needed statistics, then setting up a stratified random sample requires little more than some careful database manipulations and spreadsheet calculations.

But for researchers trying for the first time to measure the size of a market, or to determine market shares or other quantitative information, finding the right statistics can be a problem.

At least four solutions are available to the researcher who needs the economical efficiency of a stratified random sample, but who does not have the benefit of an existing database describing the relevant market.

1. Statistics texts usually recommend that a small "pilot survey" be conducted in advance. Even a relatively small survey can provide a rough estimate of the statistics needed, and this can be far better economically than using a simple proportional allocation. Unfortunately, it is sometimes difficult to delay the major investigation by a few weeks to conduct a pilot survey, and allocating a budget for this type of work can pose a special challenge.

2. Sometimes one can calculate the needed statistics from data collected in a survey of a similar market. For instance, if no information were available on the distribution of patient monitors among U.S. hospitals, the researchers might have looked for a database of some other product with some similar market characteristics. For instance, survey data for some types of ultrasound equipment, infusion pumps or advanced operating room devices might have been substituted, at least for the first survey, to find estimates of the required statistics.

3. Begin the survey using a simple proportional allocation plan, and gather the required statistics as the data comes in. This approach requires some very quick handling of survey data, especially if the surveying process is providing many new answers every day. Still, the analyst can perform calculations on the available data every day or two, and make periodic decisions about when to cut off surveying in each market segment. The method described here can only work if there is a great degree of randomness among the early respondents - the analyst would not want to stop telephone surveys to small hospitals if, for example, only the West Coast had been called. (This technique would be difficult to apply to a mail survey, unless one has the luxury of sending out mailings in waves.)

4. Simply use a rough guess about appropriate sample sizes, and plan to improve on the allocation method the next time the survey is conducted. For example, there are probably many medical equipment markets like the patient monitors example, in which sales and usage are more diverse among large hospitals than among small ones. If the researcher thinks that the market to be studied has this characteristic, then there is probably something to be gained by using a sample allocation matching the one shown in Fig. 4. Recognizing this, a market researcher might arbitrarily allocate more of the sample to large hospitals, and less to small ones, and hope for the best. The advantage of this approach is that it is very easy and inexpensive; the disadvantage is that it simply does not take full advantage of the methods of stratified random sampling.

Conclusion

Stratified random sampling is a technique that can give some dramatic benefits, by lowering the cost of surveys such as the patient monitors project described here. As was pointed out in this example, proper stratification of the sample can save hundreds of telephone interviews among surveys of hospital markets.
The techniques used for stratification also help solve some of the questions many researchers have about the accuracy of the results they have worked so hard to gather. Market analysts with a strong quantitative background can master the statistical calculations involved, and finish their research investigations with much greater confidence in the meaning of the results.

The information presented here applies to almost any quantitative survey - not just to hospital markets for medical equipment. Stratifications by geographic region, customer size, purchasing method, age, sex, urban/rural setting, and many other categories are common in market research. In each case, the researcher has decided to use these statistical techniques to gain the benefits of accuracy and economics in conducting market research. Properly applied, stratified random sampling gives the researcher a much higher level of confidence in survey results and conclusions, making market research a more reliable and effective activity in any industry or application.

References

Statistical Concepts and Methods, G. K. Bhattacharyya and R. A. Johnson, John Wiley & Sons, New York, 1977.

Some Theory of Sampling, W. E. Deming, Dover Publications, New York, 1966.