C. Ying Li is a market research analyst with the New York State Electric and Gas Corp.
Home-ownership has always been an important element of the American economy. The housing industry has grown tremendously in the 1980s. Prices for homes in some areas have more than doubled since the last census. The 1980 Census collected housing data for the entire housing stock (including old and new, for-sale and not-for-sale homes) for different geographic areas. However, only the National Association of Realtors regularly collects home-buying data for the post-censal period. Geographic coverage is limited to only selected metropolitan areas. As a result, researchers still rely on the 1980 Census housing data for the full picture. It would be desirable to work with data having the same breadth and depth as in the census, but reflecting more recent changes.
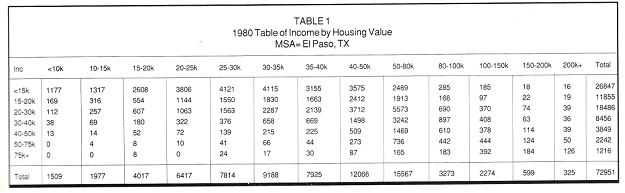
This article describes a way to analyze the table of households cross-classified by housing value and housing income from the 1980 Census by using the logit response model. The estimates so obtained can be used to approximate a more current table. The table for El Paso , Tex. (Table 1) from the 1980 Census serves as an example. In this table, there are seven row categories for household-income and 13 column categories for housing value. The housing units are defined as owner-occupied, single-family homes.

The logit response model is based on least squares regression. First, frequency data must be transformed because the regression method requires continuous and normally distributed data.
The frequency data are transformed into "logits" by a logit function (natural logarithm of the probability ratio). Then the variance of the logits is weighted to achieve asymptomatic normality. The specific regression technique applied to the set of logit data is weighted covariance analysis. Final logit estimates can be converted to cell probabilities for prediction.
A prerequisite for the logit response model is that there be a causal relationship between the two variables being analyzed. In the present case, the income variable is the "cause" (or the explanatory variable) and the housing value the "effect" (or the response variable). The income variable must be ordinal.
If the logits or converted probabilities from the fitted model match the original data closely, researchers can then use them for short-term forecasting, assuming that the short-term relationship between income and housing value remains constant. Long-term projection is not advisable because this relationship may change over time.
Data transformation
Counts are transformed into logits by the logit function. The logit function is the natural logarithm of the odds function. Therefore, logits are equivalent to "log odds." The first thing to do is to take the ratio of any two non-zero probabilities to produce odds. The odds are a positive value between zero and infinity. If I order all the odds derived from a table from the smallest to the largest, then plot them on a straight line, there would be a cloud of random points stretched out at the upper tail toward positive infinity, and bunched in at the lower tail near zero. However, by taking logarithms over these odds, the upper tail of the points can be shortened and the lower tail lengthened, making the data more compact and evenly distributed for modelling.
A small 2x3 table will be used to illustrate the logit function in detail. Suppose that this table is population cross-classified by income and education, as in Table 2:

There are two numbers in each cell: (1) the number of people, and (2) the probability relative to the row total. Each row category is treated as a separate population, and the response probabilities of individual cells are calculated by dividing the cell counts by the corresponding row total. The two populations in Table 2 are: (1) the 10 people with income less than $10,000, and (2) the 20 people with income more than $10,000. To calculate the odds, I contrast each cell response probability with that for the last response category. There are a total of four odds for this table: 2.5, 1.5, 0.36, and 0.45. The two odds in row 1, 2.5 and 0.36, can be interpreted as: the numbers of ">=$10,000 income" category are 2.5 times more likely to have an elementary school education than to have a college education, and 1.5 times more likely to have a high school education than to have a college education. The total odds for a population should always be one less than the total response (column) categories.
When I must divide numbers to obtain odds, the results are no longer linear (or additive). Nonlinearity causes the odds to fluctuate wildly. After taking logarithms of these odds, they become "linearized." The linearized logits (or log odds) are additive and manageable in size. Table 3 lists the odds and logits for my data:

There are two numbers in each cell: (1) the odds, and (2) the associated logits in parentheses. The linearity property of the logarithmic function is embodied in the minus signs of the expressions in the third column of Table 4.

After the logit transformation, the old column (education) categories are no longer meaningful for the new columns. I assign a new variable, the "Logit group," to the two new columns. The data in each logit group can be modelled separately. There are two logits for each logit group, allowing me to fit a linear equation. I can conceivably fit a polynomial equation if there are more than two logits. The single mathematical expression for the two linear equations is:
Logitij =b0i + (bli * xj) + eij
where i=1, 2 logit group; j=1, 2 income level; b0i, b1i are the intercept and slope parameters to be estimated; and the random component eij. x j is the explanatory income variable. The two sets of logits available for modelling the two equations are:

Note: (*) $5000 is the middle value of the "<=$10,000 income" category, (**) $18,000 is an arbitrary income value assigned to the open-ended ">$10,000 income" category.
For my original example of the income-by-housing-value table (dimension: 7x 13), there should be a total of 84 logits (see Table 6). Within each of the seven income populations, there are 12 linearly independent logits; that is, their values are not dependent on each other. This independence allows me to develop models for the 12 logit groups separately, with the assurance that the probabilities derived later add up to unity for a population. This is not possible if I use the 13 response probabilities directly for modelling.

Unfortunately, taking logarithms does not generate logits with equal variance. The logits are usually not distributed normally at every income level. In the following sections, I will discuss ways to correct these two conditions to meet the assumption for ordinary least-squares regression.
Some distributional considerations of logits
Logits, continuous but non-normal, are based on frequency data that are multinomially distributed. When the sample population from a multinomial distribution is large, the continuous normal distribution can be used to approximate the discrete multinomial distribution. A multinomial population of size n with probability of p for level 1, and q for level 2, can be approximated by a normal distribution with mean n*p, and variance n*p*q.
When researchers must choose between parameter estimates from a regression model, the estimates with smaller variance (even if they are biased) are always preferred to those unbiased ones with larger variance because the former provide better confidence in prediction. The ordinary method of least squares can produce the optimal estimates only when the data have equal variance. With unequal variance in the data, one must rely on weighted least squares to minimize the size of modelling error, maximize the significance of the model, and consequently yield estimates with smallest variance. The weight appropriate to my regression is the variance of the logits, npq. The calculated weights indicate the relative accuracy of the data: more importance is attached to the logits with larger probabilities, and less importance to the logits with smaller probabilities. They are proportional to the reciprocals of the variance of the individual logits. Therefore, an original variance of, say, v would be v/(npq) after weighting.
Method of least squares regression
The specific method of least squares regression is weighted covariance analysis. Covariance analysis is a way to combine both regression and analysis-of-variance techniques. The idea is to regress logits on income separately for the 12 logit groups, and then use the results for determining the income effect. For each regression equation, I have seven logit responses for the seven income levels. Polynomials are usually the model for characterizing the income-logit relationships. All 12 polynomial regressions for the 12 logit groups should have the same degree of power. A covariance analysis can estimate the regression coefficients and test the hypothesis that the coefficients (be they linear or quadratic) are constant across all logit groups. If the test indicates any difference, then there is an interaction between the logit groups and incomes.
An SAS program that produces a weighted covariance analysis of the logit data for El Paso is shown in Table 7:

With a few statements, SAS is able to fit 12 quadratic regressions for the 12 logit groups simultaneously. In this program, "inchouse" is the name of the dataset that contains the logits; "income" is the income variable; "w" is the weighting variable. Since income is the explanatory variable, its values must be continuous. For all levels except the highest open-ended category, I choose the middle values to represent the income categories. For the open-ended (the over $75,000) category, I merely choose a reasonable income value for regression.
The regression statistics from running the SAS program are shown in Table 8.

This model has a high overall statistical significance of 0.99 R-square. The overall covariance of variation (root mean square divided by response mean) is moderately high at 19.35%. Type I sums of squares measure the contribution to the model by individual model components. The amount from the NLOGIT source is the contribution due to the different logit groups; the amount from the INCOME*NLOGIT source is the additional sum of squares due to the different "linear" regression coefficients (as specified by the NLOGIT variable); the amount from the INCOME2*NLOGIT source is the contribution from the different "quadratic" coefficients. The associated tests confirm that all components are highly significant to the overall model (the probability of seeing nonsignificance is 0.001—virtually zero). Therefore, I have correctly specified the logit-income relationships by fitting quadratic equations.
Figure 1 is a sample plot of logits against income for one of the logit groups. In the plot, I overlay the actual logits over those predicted to demonstrate the close fit. (The symbol for actual logits is "0", and "x" for the predicted logits). SAS automatically converts the estimated logits to probabilities. These probability estimates will be used for prediction.

Using the results from the model
If I wish to estimate the 1981 income-by-housing value table from the same table of 1980, I need:
- the 1980 income-by-housing-value table (hereafter called "1980 I x H" table),
- the estimated probabilities from the logit response model based on the 1980 I x H table,
- the 1980 household-income-distribution table (hereafter "1980 I" table), and
- the 1981 estimated household-income-distribution table (hereafter" 1981 I" table).
The 1980 I x H, 1980 I, and 1981 I tables are available from most demographic data suppliers.
I first divide the total count of the 1980 I x H table by that of the 1980 I table to obtain a percentage that represents the proportion of households owning houses to all households. This percentage is assumed to be identical for all income levels, meaning that households at every income level have approximately the same probability of owning houses. To estimate the 1981 income-by-housing-value table, I then multiply this percentage by the seven marginal household counts (for the seven income levels) from the 1981 I table. The result becomes the seven marginal household counts estimates for the 1981 income-by-housing-value table. Finally, I multiply these marginal counts by estimated cell probabilities to obtain the counts for individual housing-value levels.
This logit model for a two-dimensional table can be easily applied to a multi-dimensional table. The only difference is that I must specify one dimension to be the response variable, and the rest to be the explanatory variables. I can then build a large covariance analysis model, with as many regressors as the number of explanatory variables. Such an expanded model, if possible, would allow me to include more factors than income for predicting the housing-value distribution.
Discussion
Although the logit response model is an effective tool for analyzing large cross-classified tables, it has problems too: (1) the error of the original model before linearization may be larger than that of the linearized model, and (2) it does not work well with sparse tables with too many empty cells.
Before the logarithmic transformation, the original model is the "odds" model: odds= p/(1-p), where p is the probability, and has an unknown, multiplicative relationship with income. After computing the logarithms, the odds becomes the logits that has a linear relationship with income:
logit = log(odds) = log p - log(l-p) = b0 + bl * x1 + b2 * x2 +...e.
This logit model is linear in its parameters b0, b1, b2. However, it is not linear in the unknown parameters of the original odds model. For example, if the logarithmically transformed error, e, is normally distributed with mean zero and variance v, then the error term in the original odds model must have a much more complex distributional form. All that is known is that this distribution is a function of e, and is therefore likely to be larger than e. In other words, the original model may be statistically complicated enough to warrant further adjustment, although the transformed model has a simpler structure.
The logit response model is not suitable for analyzing sparse tables, especially those for small areas. Since the logarithm of a near-zero value is negative infinity, the covariance matrix for fitting the curves is likely to be singular and produces no solution for the parameters. If there are not too many empty cells, two things can be done to avoid the problem of singularity. (1) Replace the empty cells by 1/(r*ni) where r is the number of response levels, and ni is the row total that contains the empty cell(s). (2) Assign a reasonable yet small number, say, 0.5, to all empty cells before calculations. It is not advisable to eliminate empty cells by combining levels. Valuable information may be lost through such an approach.
In conclusion, if a researcher is only interested in estimating a table for a fairly large area and for a year not far from 1980, the logit response model should serve his or her needs adequately.
References
Rudolf, J.F. and Ramon. C.L., SAS For Linear Models, (1981), SAS Institute Inc.
Shyrock. H.S. and Siegel. J.S., The Methods and Materials of Demography, (1973), The Bureau of the Census.
Snedecor. W.S. and Cochran. W.G., Statistical Methods, seventh edition, (1981), Iowa State University Press.
Velleman. Paul F. and Hoaglin. David C., Applications, Basics, and Computing of Exploratory Data Analysis, (1981), Duxbury Press, Boston .
Warren . G., Statistical Modelling, (1984), John Wiley & Sons.