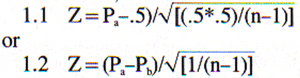Michael H. Baumgardner is vice president/executive director of Burke Marketing Research's Information Services Division. Baumgardner has worked in the area of marketing research and statistics for over 10 years. He has a Ph.D. and masters degrees from Ohio State University. Ron Tatham is president of Burke Marketing Research. Tatham, formerly professor of marketing at Arizona State University and the University of Cincinnati, has worked in marketing research for over 15 years. His Ph.D. is from the University of Alabama. Both Baumgardner and Tatham have published extensively in marketing related books and journals. Burke Marketing Research is a division of SAMI/Burke.
Simple paired comparison tests of preference are one of the most common experiments done in marketing research. For example, two products, A and B, are presented to respondents and they are asked which they prefer either on an overall or attribute specific basis. We will call the proportion of people preferring A, Pa and the proportion preferring B, Pb. Our goal is to determine whether a significant difference exists between P1 and Pb.
Binomial problem
Most reference texts treat this as a binomial problem, that is, only two responses are possible. Consequently, either the binomial test or a Z-test (or equivalent X2) would be applied. Under the null hypothesis that Pa = Pb = .5, the common Z-test is seen in several forms, such as:
Generally, Yates correction factor for continuity is incorporated into the Z-test, but we will ignore that detail for our discussion.
Unfortunately, the reference text wisdom fails to recognize that, as a practical manner, the paired-preference is most often not a binomial problem. Respondents will not only "prefer A" or "prefer B," but will also at times indicate they "don't know" or "have no preference." Thus, the typical marketing problem yields a trinomial distribution of responses: Pa, Pb, and Pc where Pc represents the proportion of respondents who indicate they have no preference.
If we have a trinomial distribution, the variance of Pa - Pb can be shown to be [Pa + Pb - (Pa - Pb)2]/
(n - 1). Since, under the null hypothesis, we can assume that Pa = Pb, then the variance
becomes [Pa + Pb]/(n-l) and the Z-test for testing significance becomes:
Many researchers do not use 1.3 for significance testing. In-stead, in the presence of "no preference" responses, researchers will commonly choose one of the options described below:
Option 1: Split the "no preference" responses evenly between the two products in the paired-comparison test.
Option 2: Split the "no preference" responses proportionately among the two products in the paired-comparison test, i.e. , proportional to the observed preference among those who had a preference.
Option 3: Throw away the "no preference" responses and reproportion on the smaller base of those stating a preference. They will then proceed to treat the problem as a binomial one and apply either 1 . 1 or 1 .2.
We will illustrate the implications of all this by examining the following hypothetical data from a paired-comparison study involving 100 respondents:

Option 1: Split the "no preference" responses evenly between the two products in the paired-comparison test.
Splitting the 20 "no preference" respondents equally gives us the following data:
Option 2: Split the "no preference" responses proportionately among the two products in the paired-comparison test, i.e. , proportional to the observed preference among those who had a preference.
Splitting the 20 "no preference" proportionally gives us the following data:

Option 3: Throw away the "no preference" responses and reproportion on the smaller base of those stating a preference.
Eliminating the 20 "no preference" respondents gives us the following data:
Conclusions: We believe the trinomial approach is fundamentally correct and recommend that to our clients. In practice, this is almost1 identical to eliminating the "no preference" responses and reproportioning on a smaller base.
Splitting the "no preference" respondents equally will reduce sensitivity, and frankly, we feel uncomfortable giving a consumer a response that we make up. Splitting no preference respondents proportionally is especially dangerous, since it can easily lead you to conclude products differ when in fact they don't.2
Notes
1 We say "almost" because it is not mathematically equivalent when using n-1 rather than n in the standard error calculations.
2 Also, in both these latter approaches the "correct" variance estimate is more complex than the formulae imply.