Tony Babinec is a market manager at SPSS Inc., a company that writes and markets software for market research and analysis.
Multidimensional scaling (MDS) is a very useful technique for market researchers because it produces an invaluable "perceptual map" revealing like and unlike products, thus making it useful in brand similarity studies, product positioning, and market segmentation. We motivate the use of MDS using a popular example, namely distances between U.S. cities. We then show its use in an example involving soft drinks.
Metric MDS on distances
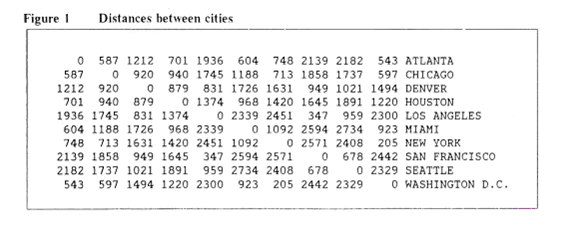
Suppose you were given a map of the United States showing the positions of the following 10 cities: Atlanta , Chicago , Denver , Houston , Los Angeles , Miami , New York , San Francisco , Seattle , and Washington , D.C. Then, with a suitably scaled ruler, it is a straightforward task to transform the information in the map into a square array of distances between all pairs of cities. See Figure 1.

In the above distance matrix, every row and column corresponds to a city. For example, Atlanta is the first row and column. The diagonal is filled with zeros, since a city is no distance apart from itself. 587, the distance between Atlanta and Chicago , is found at the intersection of the first row and the second column or the second row and the first column.
Suppose that you were given the reverse task. That is, start with a square array of distances between cities and assume that you are geographically naive and don't know their relative positions. Then, given the distances, you must represent the cities in a low-dimensional plot so that, as much as possible, the distances between cities in the low-dimensional plot resemble the distances between cities in the actual distance matrix. It might take one, two, three, or maybe more mathematical dimensions to adequately represent the distances between objects. In a nutshell, this is the type of problem that can be solved by the technique of multidimensional scaling.
If we apply ALSCAL—one of a number of popular MDS programs—to the square matrix of distances between cities, it produces the plot shown in Figure 1b.

Examination of the plot reveals that the array of cities in the plot resembles the position of the cities on a map of the United States . City 6, for example, is Miami , which we know can be found in the southeast comer of the United States at the southern tip of Florida . Opposite Miami is Seattle , point 9 in the plot. The placement of the axes in this plot is arbitrary, although by coincidence they correspond roughly to east-west and north-south directions.
Several measures of goodness-of-fit help quantify how much distances between points in the plot emulate distances between cities. For example, one such measure, S-STRESS, should be near 0 when fit is good, and the S-STRESS measure for this plot is 0.003, which is very good.
In arriving at our MDS solution, we specified to ALSCAL that the distances in our distance matrix have ratio measurement properties. As an example, Chicago and Denver are 920 miles apart, while Chicago and San Francisco are 1,858 miles apart. The ratio of 1,858 to 920 is a little over 2 to 1, and we say that San Francisco is twice as far from Chicago as Denver is. Since the S-STRESS measure in our analysis indicates very good fit, the distances between points 2 and 3 and points 2 and 8 in Figure 1b very much represent this ratio property of the distances between cities in the actual distance matrix.
Nonmetric MDS on ordinal dissimilarities
Suppose you assemble a small panel of experts. You don't expect them to know actual distances between cities off the top of their heads, but you do expect that they have some sense of whether cities are close or far. You instruct your panel that when you name a pair of cities, they are to use a 1 to 9 scale to specify whether the pair are close together or far apart.
Suppose this exercise produces the dissimilarity matrix shown in Figure 2 ("dissimilarity matrix" refers to the fact that a large number means a lot of dissimilarity while a small number means a little dissimilarity):

These dissimilarities are now not actual distances. If a pair of cities is rated as being a 9—that is, very far apart—and another pair of cities is rated as being a 3—that is, fairly close—it is not correct to say that the first pair is 3 times as far apart as the second pair. In other words, these dissimilarities do not have actual distance properties, but instead have ordinal measurement properties. Nonetheless, this is where MDS is extremely useful, for we can specify that the dissimilarities be treated as ordinal measurements and have ALSCAL produce its map.
The resultant map is shown in Figure 2b:

The S-STRESS measure from this solution is 0.07, which is still very good. Comparison of Figure 2b, derived from ordinal dissimilarities, with Figure 1b, derived from actual distances, shows very little difference between the two analyses in recovery of actual distances.
A soft drink example
Figure 3 shows a matrix of dissimilarities involving colas:
The particular colas are Diet Pepsi, Royal Crown, Yukon , Dr. Pepper, Shasta, Coca Cola, Diet Dr. Pepper, Tab, Pepsi, and Diet Rite Cola. The data come from Schiffman, Young, and Reynolds' book entitled "Multidimensional Scaling." In their

book, they present individual subject data. The data in Figure 3 are averages of all the individual subjects' dissimilarities. The data are from some years ago, and thus do not necessarily reflect the present-day market. Note that the dissimilarities are on a 0 to 100 scale, where low scores indicate similar colas and high scores indicate different colas. As examples, Shasta and Pepsi were perceived to be similar, as their average dissimilarity is 22.6, while Dr. Pepper and Coca Cola were perceived to be very dissimilar, as their average dissimilarity is 90.
We ran an analysis of these dissimilarities using an ordinal solution in ALSCAL. This produced the plot in Figure 3b:

In this type of MDS, no special meaning is attributable to the axes in the plot. You must examine the plot and note which points are near to or far from which other points. For example, the sugar-free colas, represented by 1, 7, 8, and A, are on the right, while the sugared colas are on the left. The "cherry"
flavored drinks (this study occurred before Cherry Coke was launched), represented by point 4 (Dr. Pepper) and point 7 (Diet Dr. Pepper), are along the bottom, suggesting that the bottom-to-top direction is a cherry-noncherry axis. Among the sugared colas, Royal Crown, Shasta, and Pepsi are all perceived to be similar. Yukon , perhaps tasting sweetest, is a small distance away from these three, while Coke is off by itself.
Given the information in Figure 3b, a marketer at Pepsi might take steps to differentiate Pepsi from the other colas. A marketer at Coca Cola (or some other company, for that matter) might have noticed that Dr. Pepper has one area of the map to itself, suggesting an entry of a cherry-flavored drink by Coca Cola (if not someone else) into the market.
Useful points to know in applying MDS
The following are some useful points to know in applying MDS.
MDS works well in situations where subjectivity enters, such as eliciting of taste, smell, and perceptual judgments. This is in contrast to other techniques such as conjoint analysis (see Joseph Curry's Data Use article "Understanding Conjoint Analysis in 15 Minutes" in the June/July 1989 issue Quirk's Marketing Research Review) which elicit respondent preferences regarding hard, objective attributes, such as preference for a car having either 2 or 4 doors.
A strong plus of MDS is that it assumes that the subject evaluates the object on all relevant characteristics without the researcher having to list them. In the cola example, the subject tastes two colas at a time and is asked whether they differ in taste a little or a lot. Presumably, the subject tastes the difference, whether it is a difference in sugariness, saltiness, cherry-ness, or whatever. In this, MDS differs from many other techniques which require the researcher to enumerate and include all relevant attributes or variables, and in which omission of an important variable from the study can fatally bias the results. On the other hand, if you have measurement of specific external attributes, you can determine whether objects differ on these attributes through property fitting, which fits a vector along which objects vary in the perceptual map produced by MDS.
Another virtue of MDS is that it does not require that the input to the technique be quantitative data. As we have shown, MDS can take as input dissimilarities about which we make no stronger than an ordinal assumption. This is a very nice feature, as in market research, psychometrics, and many other areas, we often cannot do better than measure along ordinal scales.
The researcher can vary the number of dimensions in the solution until a suitable fit is attained. While a two-dimensional solution often works, sometimes three or more dimensions might be necessary to adequately represent dissimilarities between objects.
No special meaning is attached to the placement of the axes in the perceptual map. Given a good fit, the researcher examines the array of points in the plot and sees which objects are near to and far from which other ones, regardless of compass direction in the plot.
Finally, there exist many versions of MDS. In individual differences scaling, the individual subjects' dissimilarity matrices are not averaged but are read in "stacked" form. The resulting analysis allows for individual differences in perception. For example, one subject might be very sensitive to differences in saltiness in products being rated, while another subject might not sense variation in saltiness across products.
In unfolding models, the input to the analysis is a rectangular matrix in which rows represent subject, columns represent brands or products, and the elements in the matrix are preference ratings (a low score means "prefers a little" while a high score means "prefers a lot"). The resulting perceptual map places subjects close to brands/products they prefer and far from brands/products they do not prefer.
Conclusion
Market researchers can often only measure at the ordinal level. The respondent can successfully rate items as being similar or dissimilar using a scoring scheme about which the researcher is unwilling to assume distance or ratio properties. These data can be used by the market researcher to assess how a particular product or brand relates to others. Multidimensional scaling is a powerful tool which produces insightful plots for determining brand or product position, or for finding market segments. Multidimensional scaling is available in software such as SPSS-X from SPSS Inc.