Editor's note: Thayer Allison is research manager with Compassion International, Colorado Springs, Colo.
Many enterprises depend on long-term relationships with clients. Banks, insurance companies and many non-profit organizations provide a service or benefit that is realized over a long period of time. In return their clients or donors send in regular payments - usually called premiums - to the organization.
For such organizations there are two parts to the growth equation: acquisition of new clients and retention of existing clients. Much attention is given to the acquisition of new clients, but retention studies are few.1 This article presents a method of measuring and analyzing retention of sponsors in a child sponsorship organization.
Compassion International is a Christian non-profit organization that provides a wide range of benefits for about 18O,OOO children in 22 countries around the world. Compassion has been linking sponsors from the U.S. with needy children around the world since 1952.
Potential sponsors are made aware of Compassion's ministry through word of mouth, magazine ads, radio, TV, and other means. When a person agrees to become a sponsor they are linked to a specific needy child. The sponsor receives letters from the child as well as periodic updates from the project about the child's progress. The sponsor sends $24 each month to Compassion to provide for these benefits for the child.
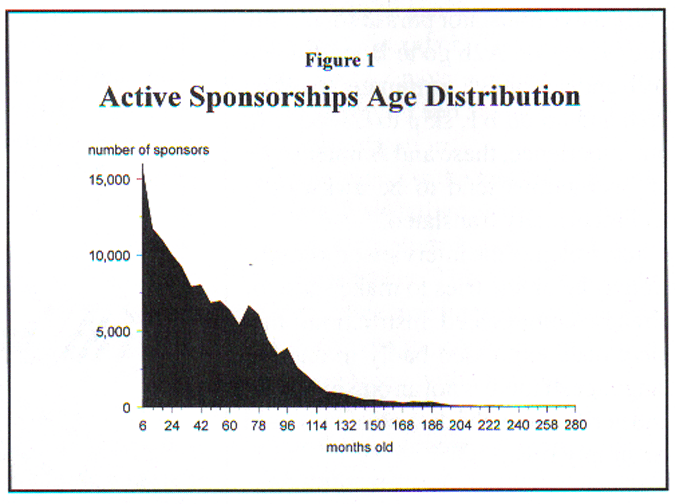
How long does the typical sponsorship last?
The question of interest for this article is: How long does the average sponsorship last? It seems like a simple question but once one delves a little deeper it is not so simple.
The most popular statistic used to describe the "typical" case when the distribution is highly skewed is the median, the middle value. The distribution of Compassion's sponsorship tenures is extremely skewed. (See Figure 1). There are many sponsors who are in the early months of their tenure. But there are some sponsorships that have lasted 12, 15 or even 20 years! These few cases with such extreme longevity pull the arithmetical mean up considerably. 
A case can be made for using mean longevity since the mean is more accurate than the median in calculating expected income. But to get an accurate estimate of the mean you must look at cohorts of sponsors who began long ago. The further back in time you go, the more accurate the estimate of the mean. But the further back you go, the less confidence one can have that the estimate is accurate for sponsors entering today.
Besides the issue of which statistic to use there are a variety of ways to group the data in measuring the longevity of a sponsorship. Each grouping has its own problems.
Median longevity of active sponsors - this is perhaps the most common measure. It is helpful but overestimates the true length of the typical sponsorship because it doesn't include the ages of all the sponsorships that have already been canceled. It underestimates the true length because all the current sponsorships haven't ended yet. They will continue for an unknown number of months. For Compassion, this median is almost 39 months.
Median longevity of canceled sponsors means all these sponsors have canceled so we know the length of time they stayed with the program. But this underestimates the typical length because it ignores all the sponsors who are still paying. For Compassion, this median is about 14 months.
Median longevity of active and inactive sponsors is probably more accurate than the other two but still has the problem of ignoring the expected future longevity of the active sponsors who haven't ended their sponsorship yet. Compassion's median longevity for active and inactive sponsors is 27 months.
Borrowing from medical research methods
The problem of estimating longevity or survival with data that has a large proportion of cases still surviving at the end of the study is one that medical researchers have faced for a long time. To determine if a medical procedure is effective they run a test on a sample of patients to see which treatment makes people live longer. But usually the test ends before all the patients have died. So the researcher doesn't know the longevity or survival time of all the patients, he only knows, for example, that 10 of his 15 patients died at various months into the treatment and that the other five were still alive when the study ended. This is called censored data. Figure 2 shows an example of censored data. Data in which the cases' starting point is at varying times is called progressively censored. 
Compassion's sponsorship database consists of progressively censored data. We know when each sponsorship started. If the sponsorship has been canceled we know their ending date too. But for a huge number of sponsorships, we only know how long they have lasted so far. How can we use all of the data to get an accurate measure of longevity?
Biostatisticians have developed survival analysis to deal with this kind of data. In statistical terminology, survival analysis is efficient because it uses all the data, not just a portion of it. Survival analysis identifies three helpful functions 2:
Survival function - sometimes called the cumulative survival rate. It an estimate of the number of cases surviving for a particular length of time. From this function it is easy to find the median life of a sample. For our purposes, I use the term "longevity function" when applied to sponsorships instead of survival function.
Probability density function - sometimes called the unconditional risk. It is an estimate of the probability of a case terminating in a certain interval. For our purposes, I use the term "expected drop-off function" or simply "drop-off function" when applied to sponsorships.
Hazard function - sometimes called the conditional risk. It is an estimate of the probability of a case terminating in a certain interval given that the case has already survived up to the start of that interval.
Using survival analysis methods on our sponsorship data
The information services department of our organization provided a dataset with records for cohorts of sponsorships. Each record included the starting month and year, the paid through month and year, the type of sponsorship, the source of the sponsorship (TV program, magazine ad, volunteer, etc.), the status of the sponsorship (active or inactive), and the number of sponsorships in that cohort.
Table 1 - the data
| begin date | paid-through date |
sponsership type |
sponsorship source |
status | count |
| May 89 | April 91 | I | A | i | 12 |
| May 89 | Aug 93 | I | A | a | 14 |
| May 89 | Jan 92 | II | B | a | 5 |
| Jun 89 | Jan 92 | I | B | i | 11 |
| . | . | . | . | . | . |
| . | . | . | . | . |
This period of longevity, the status variable, and other categorical variables were used in the survival analysis module in SPSS. SPSS produces a life table that includes all the above survival analysis functions plus the standard errors for each. SAS also produces life tables: Under the "lifetest" procedure choose the method = life option.
Potential pitfalls
There are several things to be careful about in preparing data for survival analysis. The data must be complete. A time period must be selected for which information on all the cases that started during that period is available.
At one point we discovered we had information on many cases that started before 1988. These cases showed significantly greater longevity than cases beginning after January 1988. This was because the sponsorships that had begun and ended before 1988 were not in our data. They had been "left behind" when a new computer tracking system was implemented. Hence, we had to limit our study to cases beginning after 1988.
A second potential pitfall is the designation of which sponsors are active and which are inactive to the software. You must tell the survival analysis module which value in your status variable indicates that the case has experienced the terminal event - cancellation in our case. It could be a zero or a one or any number. In SPSS you must recode nominal variables to numeric ones. The recoding begins with I, not 0, and proceeds alphabetically. Be sure you get it right. In SAS's lifetest procedure, you must indicate which cases are censored rather than which cases have terminated.
Interpreting the results
Figure 3 plots the longevity (survival) function for all sponsorships since 1988. Notice that the percent remaining crosses the 50 percent gridline at about 41 months. This means that half of the sponsorships last longer than 41 months and half have dropped out prior to 41 months. 
Figure 4 plots the dropout function for all sponsorships since 1988. The bars indicate the expected dropout rate for each month. The higher the bar, the higher the probability of a sponsorship ending in that month. The greatest likelihood of dropping out is in the first month, followed by the third month, the second month and the twelfth month. There seem to be small increases in dropout likelihood on the anniversary dates of sponsorships.

Figure 5 combines the two functions in one graph and presents information about one of several types of sponsorships available from Compassion. The line represents the longevity function and is measured on the left axis "proportion remaining." The dropout function is represented by the bars and is measured against the right axis "dropout probability."
These two functions are obviously related. In the months where there is a tall bar indicating a high probability of dropping out, the longevity line drops more. In months where the bar is short, the longevity line doesn't drop as much.
At the end of the first month ("1" on the x-axis), about 4 percent have already dropped out. By the end of the 24th month about 60 percent have dropped out. Half have dropped out by 41 months.
Figure 6 graphs the same functions for another type of sponsorship. It is clear from the two figures that longevity is considerably better for the first type of sponsorship. The expected dropout rate is almost 15 percent in just the first month for sponsorship type II whereas it is only about 4 percent for the first month of sponsorship type I. Half the sponsorships of type II have dropped out by the 13th month whereas it takes almost 41 months before half have dropped out from within type I.

Figure 7 compares the longevity of sponsorships that have been acquired through different media sources. Media source A is clearly the best in terms of longevity. Source D is clearly the worst, with 40 percent of the sponsors being canceled by the tenth month of the sponsorship. 
Longevity varies considerably according to media source. This has big implications when the organization is trying to improve its retention rate. If a large portion of the marketing budget is given to media source D, you can expect the retention rate to be drop.
Of course there are other considerations besides longevity to consider when appropriating funds among competing media avenues. The cost of acquisition for some media can become prohibitive. Some media sources can be exhausted rather quickly and even if those sources do produce long-lived sponsors, they may not produce enough sponsors to maintain the growth that is expected.
Besides looking at various groups of sponsors by source or by type of sponsorship, we can look at sponsorship longevity by year of joining. Figure 8 compares longevity for sponsors according to when they joined. Only sponsorships from media source C are considered in this graph. Longevity functions are shown for sponsorship that began in 1988, 1989, 1990 and 1991. The proportion remaining at the end of the twelfth month shows that there has been a decline in retention in each of the four years shown. About 74 percent of the sponsorship from the 1988 cohort were still active at the end of the twelfth month while only about 69 percent of those from 1991 were. Evidently longevity of sponsors from this media source is beginning to slip. Other media sources were analyzed similarly. Some were holding steady while others were slipping.
Conclusion
Survival analysis can be very useful in analyzing the retention of clients or sponsors over a period of time. It is easy to tell from a graph of longevity functions which group is lasting longer and how much longer. It is also easy to tell which months are critical months when the rate of dropping out is high. Steps can be taken to stem the loss of sponsors or clients and improve retention.
Notes
1 One of the few is "The Benefits of Customer Retention Research " by Paul C. Lubin in Quirk's Marketing Research Review from October, 1992.
2 A definitive book on survival analysis is "Statistical Methods for Survival Data Analysis" by Elisa T Lee, 1980, Belmont, California: Lifetime Learning Publications. Survival analysis is a fairly broad topic which encompasses parametric and nonparametric assumptions about the data. Statistical tests for comparing survival functions, cumulative probability functions and hazard functions for different groups are available if you need to work with samples. The current analysis was performed on the total population of sponsorships which precludes the need for concern with sampling error and all the statistical testing that implies.