Editor's note: Jay Magidson is president of Statistical Innovations, a Belmont, Mass., statistical modeling and software company. Jeroen Vermunt is a professor in the Department of Methodology and Statistics, Tilburg University, The Netherlands.
Cluster analysis has been one of the primary tools that marketing researchers have used to analyze their survey and other data to help identify different market segments. According to Kaufman and Rousseeuw (1990), cluster analysis is "the classification of similar objects into groups, where the number of groups, as well as their forms are unknown." Recent developments in model-based clustering, especially using latent class (LC) modeling offer major improvements in the ability to identify important segments and to classify persons into the relevant segment (Vermunt and Magidson, 2001). This article introduces the LC cluster model and compares its performance with traditional cluster analysis in various simulated settings.
In LC analysis, a k-class latent variable is used to explain the associations among a set of observed variables. Each latent class, like each cluster, groups together cases that are similar (homogeneous) with respect to the classification variables (attitudes, preferences, behavior, etc.). In fact, from a statistical perspective, persons in the same latent class are indistinguishable from each other in that the response patterns that describe their attitudes, preferences, etc., are assumed to be characterized by exactly the same probabilities. This differs markedly from the traditional approach used in cluster analysis of grouping together persons whose responses are "close" according to some ad hoc measure of distance (hierarchical approaches) or those that attempt to minimize within-cluster variation (e.g., k-means clustering).
The fundamental assumption underlying LC models is that of local independence, which states that objects (persons, cases) in the same latent class share a common joint probability distribution among the observed variables. Persons are classified into that class having the highest (modal) posterior membership probability of belonging given their responses. Bayes theorem is used to compute class membership probabilities, and all LC model parameters are estimated by the method of maximum likelihood (ML). Thus, the LC approach to clustering and classification moves traditional cluster analysis onto a solid statistical framework.
LC is most similar to the k-means approach to cluster analysis in which cases that are "close" to one of k centers are grouped together. In fact, LC clustering can be viewed as a probabilistic variant of k-means clustering where probabilities are used to define "closeness" to each center (McLachlan and Basford, 1988). As such, LC clustering provides a way not only to formalize the k-means approach in terms of a statistical model, but also extends the k-means approach in several directions.
LC extensions of the k-means approach
1. Probability-based classification. While the k-means clustering algorithm utilizes an ad-hoc approach for classification, the LC approach allows cases to be classified into clusters using model-based posterior membership probabilities estimated by maximum likelihood (ML) methods. This approach also yields ML estimates for misclassification rates.
2. Determination of number of clusters. K-means provides no assistance in determining the number of clusters. In contrast, LC clustering provides diagnostics such as the BIC statistic, which can be useful in determining the number of clusters.
3. Inclusion of variables of mixed scale types. K-means clustering is limited to quantitative variables having interval scales. In contrast, LC clustering can be performed on variables of mixed metrics. Classification variables may be continuous, categorical (nominal or ordinal), or counts or any combination of these.
4. No need to standardize variables. Prior to performing k-means clustering, variables must be standardized to have equal variance to avoid obtaining clusters that are derived primarily by those variables having the largest amounts of variation. In contrast, the LC clustering solution is invariant of linear transformations on the variables; thus, no standardization of variables is required.
5. Inclusion of demographics and other exogenous variables. A common practice following a k-means clustering is to use discriminant analysis to describe differences that may exist between the clusters on one or more exogenous variables. In contrast, the LC cluster model is easily extended to include exogenous variables (covariates). This allows both classification and cluster description to be performed simultaneously using a single uniform ML estimation algorithm.
The general LC cluster model
The basic LC cluster model can be expressed as:
f(yi) = ∑k p(x=k) f(yi|x=k)
while the LC cluster model with covariates is:
f(yi|zi) = ∑k p(x=k|zi) f(yi|x=k)
or
f(yi|zi) = ∑k p(x=k|zi) f(yi|x=k,zi)
where:
yi: vector of dependent/endogenous/indicators for case i
zi: vector of independent/exogenous/covariates for case i
x: nominal latent variable (k denotes a class, k=1,2,...,K)
and f(yi|x=k) denotes the joint distribution specified for the yi given latent class x=k.
For yi continuous, the multivariate normal distribution is used with class-specific means. In addition, the within-class covariance matrices can be assumed to be equal or unequal across classes (i.e., class-independent or class-dependent), and the local independence assumption can be relaxed by applying various structures to the within-class covariance matrices:
- diagonal (local independence)
- free or partially free - allow non-zero correlations (direct effects) between selected variables
For variables of other/mixed scale types, local independence among the variables imposes restrictions on second-order as well as to higher-order moments. Within a latent class, the likelihood function under the assumption of independence is specified using the product of the following distributions:
- continuous: normal
- nominal: multinomial
- ordinal: restricted multinomial
- count: Poisson/binomial
LC cluster vs. k-means - comparisons with simulated data
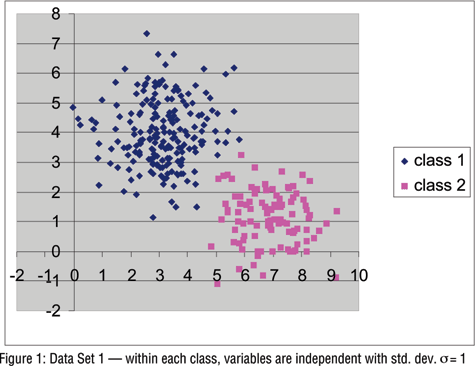
To examine the kinds of differences that might be expected in practice between LC and k-means clustering, we generated data of the type most commonly assumed when using k-means clustering. Specifically, we generated several data sets containing two normally distributed variables Y1 and Y2 within each of k=2 hypothetical populations (clusters). For data sets 1, 2 and 3, the first cluster consists of 200 cases centered at (3,4), the second 100 cases with center at (7,1).
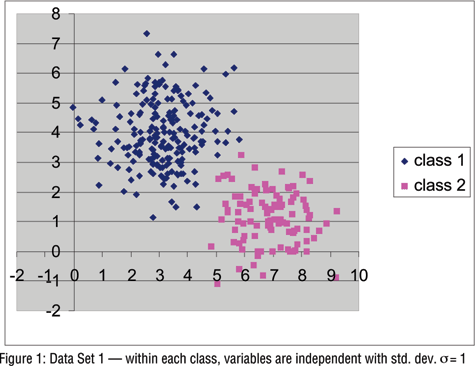 |
In Data Set 1 within each cluster the variables were generated to be independent with standard deviation equal to one. By fixing the variables to have the same standard deviation, Data Set 1 was generated to be especially favorable to the k-means approach where the variables are typically standardized to have the same variance prior to analysis.
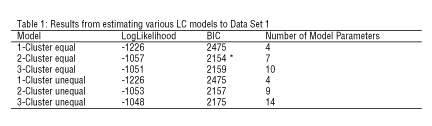
We used the Latent GOLD program (Vermunt and Magidson, 2000) to estimate various latent class models for each data set. Table 1 shows that the LC models correctly identify Data Set 1 as arising from two clusters, having equal within-cluster covariance matrices (i.e., the "two-cluster, equal" model has the lowest value for the BIC statistic, the criterion most widely used in choosing among several LC models). The ML estimate for the expected misclassification rate is 1.1 percent. Classification based on the modal posterior membership probability resulted in all 200 Cluster 1 cases being classified correctly and only one of the 100 Cluster 2 cases, (y1,y2) = (5.08,2.43), being misclassified into Class 1. For Data Set 1, use of k-means clustering with two clusters produced a comparable result - all 100 Cluster 2 cases were classified correctly and only one of the 200 Cluster 1 cases was misclassified, (y1,y2) = (4.32,1.49).
 |
Data Set 2 was identical to Data Set 1 except that the standard deviation for y2 was doubled so the standard deviation for Y2 was twice that of Y1, to reflect the more usual situation in practice of unequal variances. Figure 2 shows the greater overlap between the clusters which is caused by increasing the variability in the data.
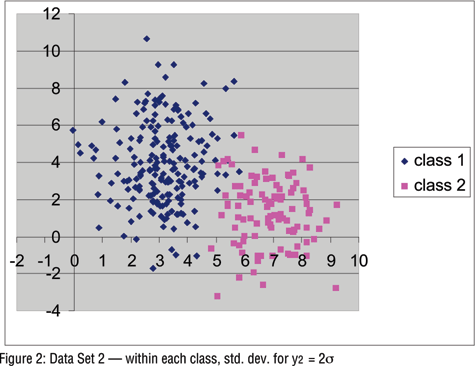 |
Table 2 shows that the LC models again correctly identified these data set as arising from two clusters and having equal within-cluster covariance matrices (i.e., the "two-cluster, equal" model has the lowest BIC). The ML estimate for the expected misclassification rate is 0.9 percent and classification based on the modal posterior membership probability resulted in only three of the Cluster 1 cases and one of the Cluster 2 cases being misclassified.
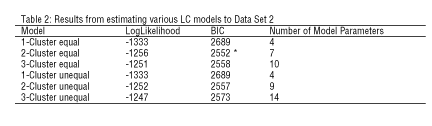 |
For Data Set 2, k-means performed much worse than LC clustering. Overall, 24 (8 percent) of the cases were misclassified (18 Cluster 1 cases and six Cluster 2 cases). When the variables were standardized to have equal variances prior to the k-means analysis, the number of misclassifications dropped to 15 (5 percent), 10 of the Cluster 1 and five of the Cluster 2 cases, but was still markedly worse than the LC clustering.
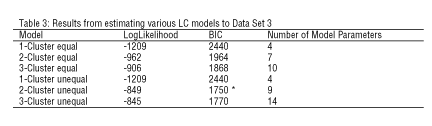
Data Set 3 threw in a new wrinkle of constructing different amounts of variability in each clusters. To accomplish this and to remove the overlap between the clusters, for Cluster 1 the standard deviations for both variables were reduced to 0.5, while for Cluster 2, the data remained the same as used in Data Set 2.
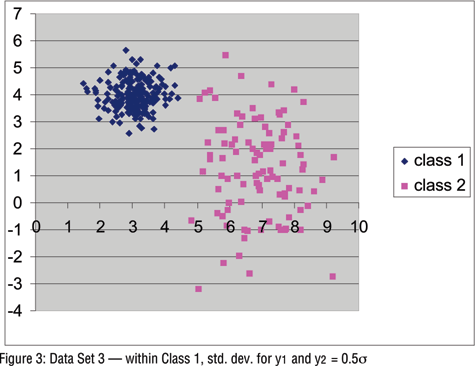 |
Table 3 shows that the LC models correctly identify this data set as arising from two clusters and having unequal within-cluster covariance matrices (i.e., the "two-cluster, unequal" model has the lowest BIC). The ML estimate for the expected misclassification rate was 0.1 percent, and use of the modal posterior membership probabilities results in perfect classification. K-means correctly classified all Cluster 1 cases for these data but misclassified six Cluster 2 cases. When the variables were standardized to have equal variances prior to a k-means analysis, the six cases misclassified based on the analysis with the unstandardized variables remained misclassified.
 |
For Data Set 4 we added some within-class correlation to the variables so that the local independence assumption no longer held true. For Class 1 the correlation added was moderate, while for Class 2 only a slight amount of correlation was added.
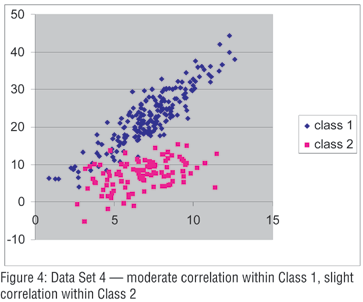 |
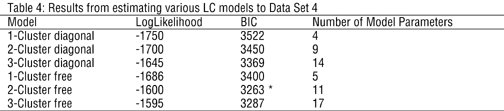
In addition to the usual LC models, we also estimated models that allowed a "free" covariance structure which relaxes the local independence assumption. While such models were not required for the earlier analyses (i.e., for the earlier analyses the BIC values were higher than that obtained using comparable models having a fixed covariance structure), such models provided an improved fit to these data. Table 4 shows that the LC models correctly identify this data set as arising from two clusters, having a "free" covariance structure (i.e., the "two-cluster, free" model has the lowest BIC). The ML estimate for the expected misclassification rate was 3.3 percent, and use of the modal posterior membership probabilities resulted in 10 misclassifications among the 300 cases.
 |
K-means performed very poorly for these data. While all 100 Cluster 2 cases were classified correctly, 44 Cluster 1 cases were misclassified, for an overall misclassification rate of almost 15 percent. If the recommended standardization procedure is followed prior to a k-means analysis, the results turn out to be even worse - 14 of the Cluster 1 and 66 of the Cluster 2 cases are now misclassified, an error rate of over 26 percent!
Comparison with discriminant analysis
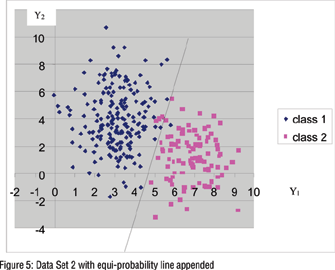
Since Data Set 2 satisfies the assumptions made in discriminant analysis, if we now pretend that the true class membership is known for all cases, the linear discriminant function can be calculated and used as the gold standard. We computed the equi-probability line from linear discriminant function and appended it to the data set in Figure 5. Remarkably, it can be seen that the results are identical to that of latent class analysis - the same four cases are misclassified! These results suggest that it is not possible to obtain better classification results for these data than that given by the LC model. For a more detailed analysis of these data see www.latentclass.com.
 |
Summary and conclusion
Recent developments in LC modeling offer an alternative approach to cluster analysis, which can be viewed as a probabilistic extension of the k-means approach to clustering. Using four data sets, each generated from two homogeneous populations, we compared LC with k-means clustering to determine which could do better at classifying cases into the appropriate population. For all situations considered the LC approach does exceptionally well. In contrast, the k-means approach only does well when the variables have equal variance and the assumption of local independence holds true. Further research is recommended to explore other simulated settings.
While this article was limited to the use of LC models for cluster analysis, LC models have shown promise in many other areas of multivariate analysis such as factor analysis (Magidson and Vermunt 2001), regression analysis, as well as in applications of conjoint and choice modeling. Future articles will address each of these areas.
Note: Interested readers may obtain a copy of the simulated data used for these examples (including the formulae used in their construction) at www.latentclass.com.
References
Kaufman, L. and P.J. Rousseeuw (1990) Finding Groups in Data: An Introduction to Cluster Analysis, New York: John Wiley and Sons.
Magidson J., and Vermunt, J.K. (2001), "Latent Class Factor and Cluster Models, Bi-plots and Related Graphical Displays", Sociological Methodology 2001, pp. 223-264, Cambridge: Blackwell Publishers.
McLachlan, G.J., and Basford, K.E. (1988). Mixture Models: Inference and Application to Clustering. New York: Marcel Dekker.
Vermunt, J.K. & Magidson, J. (2002, forthcoming). "Latent Class Cluster Analysis", chapter 3 in J.A. Hagenaars and A.L. McCutcheon (eds.), Advances in Latent Class Analysis. Cambridge University Press.
Vermunt, J.K. & Magidson, J. (2000). Latent GOLD 2.0 User's Guide. Belmont, Ma.: Statistical Innovations Inc.