Mark J. Moody is vice president/director the Consulting & Analytical Services Division of Burke Marketing Research. He has worked in marketing research and statistics for the past 12 years. His Ph.D. and Masters are from Ohio StateUniversity . Prior to working at Burke he was with the Marketing Information Dept. of Quaker Oats Company, and with Research Systems Corp.
Thanks to the publicity surrounding the recent cola wars, many consumer respondents are familiar with the basics of blinded product preference testing. "Taste Product A, and then Taste Product B. Which do you prefer?" This sort of product testing is extremely common in marketing research, whether we are working on product reformulations, new product development or advertising claim substantiation.
The interpretation of such results, however, can be quite ambiguous at times. For example, assume we are testing two alternative formulations for a new brand of oatmeal. The sample involves 250 category users and the results favor Formulation A by a 55% to 45% preference. Using a rigid 90% confidence level statistic, we would conclude there is no significant difference. Formulation A would be our best bet, but lacking a "significant" result we may be unable to convince management to "kill" one of the alternatives. (See "Statistical significance testing may hinder proper decision-making," by Michael Baumgardner and Ron Tatham in the May, 1987 Quirk's Marketing Research Review.) Furthermore, it might be argued that since 45% prefer Formulation B, both should be offered in order to cover an apparently segmented marketplace.
In fact, the question of whether different segments exist with unique taste desires is impossible to answer from these results. It could just as easily be true that the near equal results occur because most people cannot discriminate between the two products. Lack of discrimination would lead to random preferences which make products approach a 50%/50% preference. To resolve the issue of "segmented preference" vs. "random nondiscrimination" it is necessary to collect the data differently. There are many discrimination testing techniques available, but the one which deviates least from the basic preference test is to merely repeat the same unbranded pairing a second time with each respondent.
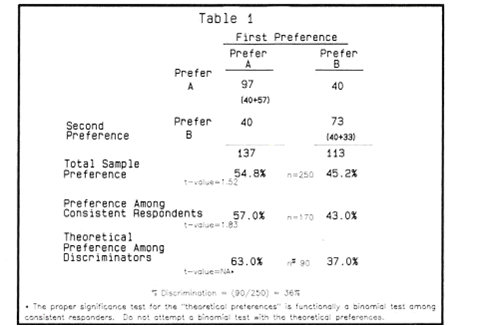
Repeat pair testing requires respondents to repeat the preference tests a second time somewhat later in the interview. Table 1 displays how these results might typically look. The key to understanding the potential of this procedure lies in the switching of preference that occurs. We see in this example 40 respondents switch from preferring A to preferring B and the 
same number shift in the other direction. A total of 80 respondents are inconsistent in their preference for some reason. The conventional wisdom is that they could not discriminate between the two products. By chance we would expect a similar number of non-discriminators to have consistently preferred one product or the other. Thus, our total estimate of nondiscrimination would involve doubling the number of inconsistent responders. In this case 160 (64%) of the 250 respondents apparently are unable to discriminate between the two formulations. (Respondents expressing "no preference" can be added to this figure.) Only 36% of the sample could discriminate, and among those we can estimate the theoretical preference for A to be 57 vs. 33 or 63.3% vs. 36.7%. The proper statistical test, however, does not involve these proportions (see below).
The logic of this approach is quite straightforward. But the assumption that as many non-discriminators are consistent by luck as there are inconsistent respondents is not necessarily true. Data collection issues such as respondents' attempts to please us, can perhaps help to exaggerate the inconsistent behavior. When product appearance differences are present, a respondent who at first picked A (though with little or no personal conviction) might wish at second preference to even the scales by switching to the other product. This possibility opens the door for more than half of the non-discriminators to be inconsistent. Solutions such as blindfolding respondents in taste tests have their own problems, since appearance may be a key component to product preference.
Fortunately it is not necessary to know precisely how many more non-discriminators are lurking in the consistent preference data in order to statistically test for a preference. The proper statistical procedure involves a simple binomial test among the subsample of all consistent respondents. In this case the sample size for the test would be reduced from 250 to 170 after discarding the 80 inconsistent respondents.
Researchers frequently are hesitant to reduce their sample sizes for fear of losing statistical sensitivity or power. It is difficult, however, to imagine how 80 respondents who can't keep their preference straight are going to help us find a reliably winning product. In fact, reducing the sample size by removal of the inconsistent respondents has the equivalent statistical effect on sensitivity of increasing your sample size! In this example the new t-value is 1.83, significant at the magical 90% confidence level (see Table 1).
The precise amount of statistical sensitivity improvement which occurs by removal of the inconsistent respondents will depend upon how many are removed. In general, the more the better. The reason is that the inconsistent respondents' random behavior serves to water down real preference differences causing them to converge 50%/50%. The penalty for having the preferences converge to equality is greater than the cost of sacrificing some of the sample size.
To better understand the process of repeat pair testing we have compiled a database of over 100 studies conducted in the past several years. Normative knowledge is valuable, even in product testing. On average we have found that starting sample sizes of 250 can have the statistical efficiency of 375 (1.5 times as much) if we first discard the inconsistent respondents. This typically means removing about 80 respondents from the original sample of 250. While the average design efficiency is 1.5, Figure 1 shows how it varies with the percentage of respondents who are estimated to be non-discriminators. The more inconsistent respondents there are to be removed, the greater the efficiency. Obviously if everybody can discriminate then there would be no added efficiency.

In our database of 119 tests we find that an additional 13 significant differences were found using the repeat pair logic, which would have been missed with more simple procedures.
The logic of removing inconsistent preferences is essentially an attempt to produce a naturally occurring "sensory panel." Most food manufacturers (and certainly all breweries) use expert taste testers at some point in their product evaluations.
Respondents who are able to give a consistent preference between two products have shown themselves to be more worthy of our efforts to please them. Repeat pair testing offers a simple method for approximating some of the skills of a sensory panel, while still testing among the real world of consumers. The statistical sensitivity gains of this procedure should not be overlooked since we frequently find nondiscrimination levels in the 60–80% range. It can be frustrating to try to find a winner when most people cannot discriminate.
Finally, when two products really are interchangeable (i.e., cost reduction reformulation) it can be very persuasive to have not only similar preferences, but also an estimate of the nondiscrimination level.