Editor’s note: Tiffany Perkins-Munn is vice president of, and Demitry Estrin is an analyst at, Marketing Metrics, Inc., Paramus, N.J.
While it is true that many firms venture into research endeavors to find data to support their a priori hypotheses, often managers have no idea what to expect. To complicate matters further, within many organizations there are various camps with different agendas and surprisingly little knowledge of their client base. It is the charge of the marketing consultant to aid in interpretation, to present the findings, to prioritize deliverables to internal clients, and to plan actions based upon the results. How can we, as marketing consultants, help our clients improve their business outcomes? What techniques can we use to provide insight to our clients - the experts - about their business?
The answer is data exploration and data mining techniques. As all of our data tends to be multivariate in interpretation, exploratory data analytic techniques can identify patterns in data sets. For example, if we want to examine the relationship between client satisfaction and profitability, our survey will obviously include questions for individual consumers that can be aggregated to a higher level (e.g., all consumers who use a particular store location) and store revenue data. Multivariate analyses will allow marketing consultants to objectively model the relationship between consumer responses, variability on store satisfaction levels and increases or decreases in profitability and to uncover patterns to predict future profitability fluctuations and strategies to prevent decreases in profitability.
Additionally, using multiple data analytic techniques to explore the data can provide us with insight on the strengths, weaknesses and unique benefits of each approach. Professor W.W. Tryon, in a 1998 American Psychologist article (“The Inscrutable Null Hypothesis”) explains, “It is difficult to estimate the handicap that widespread, incorrect and intractable use of a primary data analytic method has...but the deleterious effects are undoubtedly substantial and may be the strongest reason for adopting other data analytic methods.” Although data exploration and mining techniques are essential tools for marketing consultants, their proper use and application require reasonably sophisticated statistical training on each technique. However, the skilled marketing consultant can help even the least technically sophisticated client understand and incorporate the results into their business strategies.
Several methodological dilemmas are created by not utilizing multiple data analytic techniques. First, traditional consumer segments, such as income groups, created by the client may not be as useful for interpreting the business outcome or may not be as meaningful - in the larger picture - as the client believes them to be. Second, within segments there often exist hierarchies that impact business outcomes. For example, financial institutions tend to focus on those clients with the largest revenue potential, though not necessarily providing the largest share of wallet. Many of the “smaller” clients often complain of being treated as if they are not important. However, feedback from clients suggests that a restructuring of the hierarchy so that the clients with less revenue potential are treated like clients with more revenue potential would yield a higher share of wallet percentage for the financial institution. Third, all consumers belong to multiple segments, which makes distinction for purposes of analyses difficult. Additionally, reciprocal relationships are often not considered and every relationship is considered to be linear. Thus, a number of multivariate data mining and exploration techniques will be discussed. While there are techniques that are not listed here, we have chosen to focus on those techniques that can be used for pattern detection.
Latent factor modeling
Latent class analyses make it possible to characterize latent relationships in the data by the crosstabulation of multiple categorical variables. Latent class analysis is the categorical variable analog to the more traditionally used factor analysis. However, one advantage over traditional factor analyses is that variables may be continuous, categorical (nominal or ordinal), counts, or any combination of these. This procedure allows for the identification of a set of mutually exclusive latent classes that account for the distribution of consumers. Thus, one important use of latent class analyses is for the analysis of consumer typologies, either as a method for empirically characterizing a set of latent consumer types within a set of observed indicators or as a method for testing whether a theoretically posited typology adequately represents the data. For example, if we enter categorical data on multiple segments of the consumer group, such as major aspects of the business, along with more traditional segments, such as income and gender, we may find that there is one latent variable (e.g., face-to-face customer service) with a number of different, clearly described latent classes (i.e., high-income women who are satisfied with their face-to-face customer service or low-income men who are not satisfied with their face-to-face customer service). Alternatively, perhaps there are multiple latent variables that explain the relationship (e.g., face-to-face customer service vs. telephone customer service, vs. online customer service). A latent class analysis might suggest that there is a process that has not been explicitly captured in the survey, in addition to providing information on how this process differs for various population segments. Some marketing applications of latent class analysis include:
- identifying consumer typologies;
- identifying latent classes that explain heterogeneity within the data;
- identifying determinants of customer satisfaction that are relevant to distinct customer segments; and
- developing composite variables from attitudinal survey items.
Clustering procedures
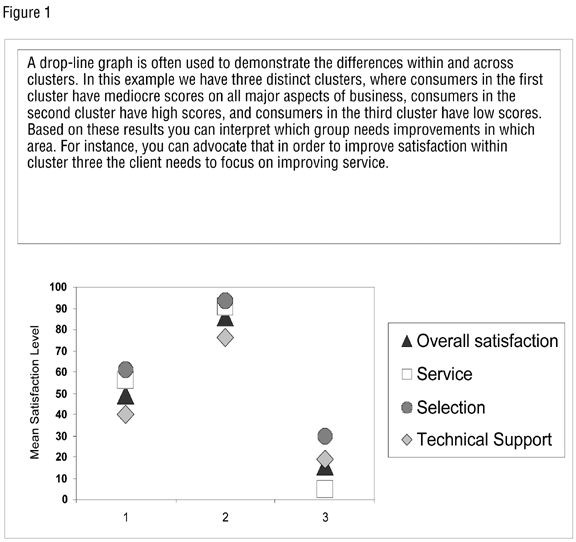
Clustering procedures are a type of relational model, one that does not assume a predictive outcome but rather investigates the relationship between all the variables. Clustering procedures are truly multivariate. For example, in client satisfaction research, we often ask a number of overall questions related to major aspects of the client’s business. Ideally, we would hope for three cluster segments: one in which consumers have all high scores on all major aspects of the business, one in which consumers have all low scores, and one in which consumers have all mediocre scores. In this simplistic example, with clustering procedures, it becomes easy for the client to identify the consumers it should on moving up the satisfaction continuum, from low scores to mediocre scores, and the consumers it should focus on moving from mediocre scores to high scores).
 |
One advantage to using cluster analysis is that the procedure does not begin with a priori well-defined segments and ask how they differ. Rather, it begins with undifferentiated segments and asks whether a given group can be empirically partitioned into segments that differ in some meaningful way. Cluster analyses are considered exploratory tools for describing, in terms of the data collected, the segment to which its members belong. Because cluster analyses make no assumptions about how segments are formed, the results may contribute to the definition of a formal classification scheme that is more meaningful than the pre-determined segments that are typically analyzed, suggest patterns with which to describe populations, indicate rules for assigning new consumers to segments for identification or diagnostic purposes, provide measures of definition change in what previously were only broad concepts, or find profile exemplars to represent a segment.
Multilevel modeling
Because consumer segments are inherently hierarchical or take on a hierarchical quality based on business outcomes, it is important for analyses to address the hierarchical structure. In other words, the existence of data hierarchies is neither accidental nor ignorable. Segments differ, with this differentiation being mirrored in various business outcomes (i.e., profitability, retention, etc.) where the outcome is often a direct result of differences between consumer segments. In other situations, the segments may be more arbitrarily constructed, such as the assignment of consumers to the local office, whereby in many instances consumers with similar demographic backgrounds live in that area. In this situation, an analysis of difference based merely on location would not be very telling. However, once segments are established, they tend to become differentiated, the differentiation implying that one group is empirically different from another. Multilevel models take into account the oftentimes hierarchical ordering of segments. Furthermore, multilevel models need not only model linear relationships. For example, in customer satisfaction research, we are not only interested in individual consumers but also in the aggregate unit, such as clients, stores, districts, regions, etc. Typically, we would investigate the individual-level effects and, in a separate analysis, investigate the aggregate-level effects. However, multilevel models allow us to understand the influence that an individual consumer exerts on the aggregate to impact the business outcome. Additionally, the ability to create cross-classification of segments in multi-level models helps to deal with the fuzzy borders of segments by recognizing that for various reasons, people may switch segments over their lifespan.
 |
Automatic interaction detection modeling
Chi-square automatic interaction detection (CHAID) is based upon the methodology of automatic interaction detection (AID) — a family of methods for handling regression-type data in a way that is robust to assumptions of linear hypothesis methods. Because CHAID only looks for interactions, it is a useful tool for analyzing multiple variables that are not easily extricable from each other (e.g., the different forums for customer service or different industries). Although CHAID is typically used in marketing data for population segmentation studies, it is one of the most powerful procedures for handling fixed-response questions that typically yield either metric or nonmetric responses.
 |
CHAID is an exploratory procedure that attempts to identify and analyze the complex relationships that may be imbedded in higher-order contingency tables by partitioning a contingency table produced from the crosstabulation of three or more variables. It does this partitioning by determining the smallest number of group splits based on significance of the group as a predictor. It then looks at the subcategories within groups as suitable predictors and continues to partition in this manner until no further suitable predictors are found. For example, a CHAID analysis may indicate that tier (an importance categorization), role (job function) and industry (business function) are significant predictors of a client’s revenue, with high-tier clients (more important clients) yielding a larger revenue percentage. However, within each of the high-revenue groups perhaps only tier and role are significant predictors and within the low-revenue groups, perhaps only industry is a significant predictor. Upon further investigation, within the low-revenue group, we may find that in certain industries, particular roles are significant predictors of revenue while others are not. This type of interaction analysis allows for further investigation into how multiple variables interact with each other to influence business outcomes and to create multiple profiles for potential business outcomes.
Curvilinear regression
Conventional linear regression assumes a linear relationship between the predictor and the outcome. That is, a straight line can best describe the relationship. To the extent that nonlinear relationships are present, conventional regression analyses will underestimate the predictor-outcome relationship. In marketing, we often have data in which the outcome can’t be predicted by a straight line. Instead, the relationship may be curvilinear. In conventional regression analyses, a partial residual plot or a component-plus-residual plot can highlight curvature of the data and illustrate non-linearities. When a curvilinear relationship exists in the data, we can fit a power polynomial to the data, the exact form of which will depend on the number of bends in the curve. Making sense of curvilinear trends depends upon whether or not a substantive explanation can be applied to a higher order relationship based on theory. For example, if we think there is one bend in the curve describing the relationship between the predictor and outcome, we’d fit a quadratic model to the data as shown in Figure 4. Consider the inverted U-theory of research and development expenditures. At the extreme — that is, high percentages and low percentages of competition — sales decrease, whereas, at moderate levels of competition, sales and expenditures are at the highest levels.
 |
Curvilinear regression analysis is carried out hierarchically. We start with the linear model and then add progressively higher order terms on successive steps (x, x2, x3, etc.) If a term produces a significant change in R2 over and above all lower order terms, we can say that the type of curvilinear relationship it represents does describe the data. Additionally, there may be multiple trends such that it may be possible to describe the relationship between the predictor and the outcome with both linear and curvilinear relationships. For example, Tim Keiningham and Terry Vavra, authors of The Delight Principle: Exceeding Customers’ Expectations for Bottom-Line Success, have illustrated this effect. As clients move up the satisfaction continuum from extreme dissatisfaction to a more satisfied state, there is a marked increase in satisfaction, after which point profits plateau until the clients reach an extremely satisfied state, at which point profits again begin to soar.
 |
Methodological and practical implications
The multivariate exploration and mining techniques mentioned above can be extremely useful for extracting additional information from your data and identifying patterns in the data in almost any research situation. The purpose of this article was not to provide an exhaustive list but rather to illustrate some of the business issues that can be addressed by utilizing various multivariate exploration and mining methodologies.
What are the implications of using multivariate exploration and mining techniques for analyzing business outcomes? The primary implication is that understanding the complex interrelationships among major aspects of the client’s business, demographics and other client-defined segmentations requires a level of specificity that multivariate statistical models can accommodate and explain. Second, in a cross-sectional design, it is difficult to determine the static and/or dynamic nature of business outcomes. Therefore, attempts must be made not only to uncover profiles and patterns at a specific point in time, but also to ultimately examine changes to profiles and patterns over the lifespan. Finally, the incorporation of all relevant variables into a unified multivariate analysis will appropriately address the evolving nature of consumer and client needs, expectations and business outcomes.