Editor’s note: Yilian Yuan is director of marketing analytics at IMS Health Consulting, Plymouth Meeting, Pa. Gang Xu is associate dean of the International Cultural Exchange Institute of Anhui University in Hefei, China.
Until the early 1970s, value expectancy models had very much dominated marketing research (Rosenberg, 1956; Fishbein, 1967). In a typical value expectancy model, consumers are asked to give a rating on an individual attribute of the product. The values derived from consumers’ ratings are combined to represent the total utility of attributes and of products. For that reason, the value expectancy models are also named componential models in a sense that the total utility of a product is derived from individual responses to the product attributes. The major concern from the value expectancy models is that consumers may not be able to differentiate the importance of attributes of a product. In pharmaceutical marketing research, for instance, a drug’s attributes of efficacy, side effects and dosing may be considered equally important to physicians.
Conjoint was developed in part to overcome this problem. Instead of asking consumers to rate the importance of each individual attribute of a product, they are presented with a list of profiles of products and asked to give a preference rating on each profile. Each profile consists of several attributes of the product such as price, efficacy and side effects, varied in its combinations among profiles. The utility of the individual attributes is derived from the values of profiles. In other words, the overall evaluation of profiles is decomposed into each utility scale for each attribute level and thus for each attribute. For that reason, conjoint is also called decomposition model.
Conjoint has been since used widely in quantitative marketing research. It has been hailed as the most innovative way of determining consumers’ true preference of products (Green and Wind, 1973, Green and Srinivasan, 1978; Louviere, 1991). (See also our article in the June 2001 issue of Quirk’s for a description of a conjoint study.) However, several limitations of conjoint pose questions and concerns among marketing researchers. First, in a conjoint study, all attributes are presumed to be the same across the products. In other words, we create profiles in which the levels of attributes for each product are the same. The levels of the attribute “price” for drug X and for drug Y, for instance, are the same. So are the levels for efficacy and side effects. We know, in reality, the prices for generic and prescription drugs vary greatly, and this is also true among brand-name products. Secondly, when we are conducting a conjoint study, we are mainly concerned about the main effects of attributes. We evaluate the differences between or among attribute levels, and are ignoring how the change of levels of one attribute may have differential impact on levels of other attributes. For instance, different brands may have different price sensitivities. In a conjoint study, we would assume that all brands have the same price sensitivity. We need to estimate, in such a case, not only the main effects but also interaction effects between brand and price, for which a conjoint study is not adequate. Another problem with the conjoint design is that, upon seeing each profile, the respondent has to give a preference rating, since “none” is not an option among the alternatives. This may cause inaccuracies in estimating utilities when respondents don’t like any of the products they see and are forced to give their preference rating. Finally, a seemingly obvious and also important one is that, when the respondents give a preference rating, it doesn’t necessarily mean he or she is going to prescribe the product. We only assume that respondents’ preference ratings can be translated into their behavior. However, there is a gap between a respondent’s indication of preference of a product and his or her actual behavior. In pharmaceutical marketing research, the respondents may be payers, physicians, patients or caregivers.
The differences between a conjoint study and a discrete choice study
A discrete choice study was thus developed to overcome these limitations manifested in a conjoint study. Discrete choice allows for the interaction effects among the levels of attributes, which is particularly useful in the estimation of price elasticity such as the interaction of brand by price. It doesn’t require that the levels be the same across the attributes. One product may have dosings (e.g., QD, BID) that are different from other products’ dosings (e.g., weekly, bi-weekly). Furthermore, a discrete choice experiment doesn’t force physicians to prescribe a product upon seeing profiles of products. Respondents can choose a “none of these” option if they don’t want to prescribe any of the products presented. More importantly, a discrete choice study asks respondents to make a choice among the alternatives presented to them, which is one step closer to reality than the preference ratings in a conjoint experiment. In a pharmaceutical marketing research study, physicians evaluate a set of drugs varied in the levels of attributes presented on the screen or on paper and indicate which drug they would prescribe. The task mimics what physicians would do virtually on a daily basis. Most marketing researchers would agree that, to understand respondents’ behaviors, we should study their behavioral intentions, not their preferences.
Technically, there is also a difference between conjoint and discrete choice modeling. Discrete choice uses the multinomial logit model, which applies the nonlinear model to estimate utilities at an aggregate level, whereas conjoint analysis applies a linear model to estimate utilities at an individual level. More about this later.
What does a discrete choice analysis do?
As in a conjoint study, the process of conducting a discrete choice study usually includes two parts: experimental design and data analysis.
A. Design
The design of a discrete choice study involves three steps: determine the number of attributes and attribute levels, select the number of choice sets and the number of respondents, and present the choice sets.
1) Attributes and attribute levels
In a discrete choice task, the respondent is presented with several choices and is asked to select one of them. The factors that influence the choice possibilities are called attributes. Each product has several attributes and each attribute has several levels. A combination of attribute levels is called a product profile. Each set of alternative profiles is called a choice set.
The attributes of a drug may include things such as price, efficacy, dosage, formulation and side effects, to name only a few. If the purpose of the study is to assess the factors that may influence physicians’ prescribing behavior of drugs, attributes are these identified factors that may exercise such influence. We may find, for instance, the high level of side effects of a drug will negatively influence physicians’ prescribing behavior of the drug. By the same token, the high efficacy of a drug may drive up the physicians’ prescribing behavior. Each attribute should consist of at least two levels. An attribute of price, for example, may have two: $10.00 and $15.00. An attribute of efficacy could have two levels: “high” and “low” or three levels as “high” “medium” and “low.” For example, if we have five attributes with two two-level attributes (drug delivery form and side effects) and three three-level attributes (efficacy, dosing, managed care plan formulary), the total number of combinations of the attribute levels is 108 (22 x 33 = 108). The number of 108 is called the total number of profiles in the full-profile factorial design. If we have three drugs with 108 profiles each, we then have total of 324 (108 x 3) profiles.
2) Selection of the number of choice sets
When there are a large number of attributes and attribute levels, it becomes unrealistic to include all possible combinations of attributes and attribute levels in a choice task. The fatigue produced by a long list of attributes and complexity of levels will lead to low quality of responses and inaccuracies of estimation. It is generally perceived that the total number of attributes in a choice set should be no more than six (Sawtooth, CBC User’s Manual, 2000) and the total number of choice sets should be no more than 30 for each respondent, since the human cognitive processing capability is limited (Miller, 1956). In most discrete choice experiments, like in conjoint, a fractional factorial design with a small number of the profiles is used. In this example, a fractional factorial design consisting of only 18 profiles out of the 108 might be used.
The question is, how do you decide the number of the profiles that are needed in a choice study? In general, there is no single rule to follow. These are the considerations frequently cited in the literature: the number of parameters to be estimated, orthogonality and balance. The orthogonality refers to a design where the effect of each attribute can be estimated independently. The balanced design refers to a design in which the levels of attributes are equally represented, so that the effects of attributes can be estimated efficiently. The number of parameters to be estimated is determined by the number of products, the number of attributes and levels. In the example we cited earlier, we have two two-level and three three-level attributes and the smallest integer that can be divided by 2, 3, 2 x 2, 2 x3 and 3 x 3 is 36. That is, we achieve a perfect orthogonality if we have a total of 36 profiles in the study. However, we know that 36 profiles are too many for respondents to complete and we have to reduce it, say, to 18. The number 18 can be divided by each of the above-mentioned numbers except 2 x 2. Here, we compromise the number of profiles in the study by having imperfect orthogonality. The balance here refers to the frequency of attribute levels appearing in the total number of profiles. In other words, ideally we need to have an equal number of attribute levels for each attribute included in the selected profiles. This is hard to achieve when we have to reduce the number of profiles in a fractional factorial design.
Fortunately, many software packages have provided the calculation determining the number of profiles that are needed. The SAS Macro procedure of %mktruns is one of such examples (Kuhfeld, 2000).
3) Presentation of the choice sets
There are many ways that discrete choice scenarios may be presented. Two popular ways are choice question and allocation. These two are very similar, except that respondents are asked to make a choice among the alternatives (choice question) or to allocate the number of prescriptions (allocation).
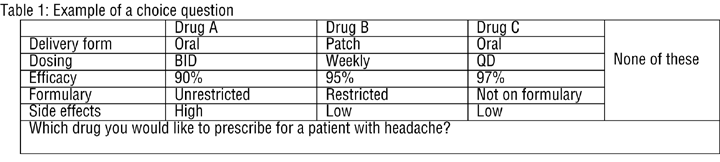
Suppose we now have five attributes and three competitive drugs for headaches. Table 1 illustrates the simplified version of the choice question and Table 2 shows allocation. The allocation approach asks the respondent to assign the number of patients/prescriptions to products.
 |
 |
Notice here that in both tables, we can include different attributes and attribute levels for each drug. For instance, for Drug A, the dosing may be QD, BID and TID. For Drug B, the dosing may be daily, every other day or weekly.
As shown in the tables, physicians are asked in each scenario to either make a choice or allocate his or her next 10 prescriptions or patients across a set of profiles. These allocations can also be made for each patient type or other situational variables such as severity of the disease and comorbidities. In presenting the sets of alternatives to physicians, we usually also present these situational variables along with the choice sets. For instance, in presenting the drug set for treating patients with headaches, we may present different types of patients: migraine, tension and cluster; or mild and severe. Also patients may vary between men and women, since migraines affect more women than men. Physicians therefore are asked to make a choice among the alternatives under each level of these situational variables. The responses to different situational variables are collected in order to assess the impact of situational variables on prescribing preferences.
As in the conjoint task, we want to reduce respondents’ cognitive burden while completing the task. The factors that could affect the respondents’ burden are the number of attributes, the number of levels per attribute, the number of brands and situational variables. Note here that if you are interested in the cross effects of attribute levels (interaction effects), you should specify these requirements in the design stage so that the number of profiles or sample size required for such needs can be met. Another way of reducing cognitive burden is to fractionalize the task; that is, divide the total number of choice sets into several subsets and each respondent only completes one subset. The data are combined and then analyzed. However, by doing so, the total sample size of respondents will increase.
B. Data analysis
The data from discrete choice are analyzed using the multinomial logit model (Louviere 1988, 1991). Note that this multinomial logit model is different from ordinary least square regression model (used frequently in the conjoint study) in that the coefficients are interpreted as the effects on the odds of choosing one alternative relative to another.
As shown in the two tables, physicians are asked to make a choice on the number of prescriptions for each product for the next 10 patients. The responses from physicians are used as the dependent variable in the logit model. The attribute levels are independent variables. The model is to assess how well the independent variables predict the physician’s choice of drugs. Specifically, from the output of the logit model, one can compute an odd ratio of a profile or individual drug chosen over the alternatives in the choice set. In addition, the coefficients can be used to compute the utility value of each attribute level and the derived relative importance of attributes.
If the situational variables are used in the task, as seen frequently in a pharmaceutical marketing research, these variables are included in the model and their impact on a physician’s choice of product are estimated. For instance, in the example cited earlier, we want to assess three drugs and evaluate physicians’ share of preference of each drug. Physicians are asked to prescribe a product for patients with different gender and severity. Gender and severity can be included in the model as independent variables and their coefficients estimated. If we know that the prevalence rate of headache for women is 70 percent compared to 30 percent of men, and if 20 percent of the headaches are severe and 80 percent are non-severe, we can weight the model coefficients to reflect these distributions and to obtain an overall share of preference of products.
Validation and simulation
Validation in a choice task refers to the estimation of how well the model can predict the actual observed values. As in a conjoint task, this is achieved through what is called “holdout” sets. These holdouts are not used for the estimation of the model. Rather they are used solely for the purpose of validation. In the examples we cited earlier, if we have a total of 18 choice sets, each has three profiles plus one “none of these” option. We may include two more choice sets as holdouts. These holdouts may include the most likely profiles of the drug the client wants to assess, along with other competitors. Since these holdouts are not going to be used for estimating the model, the responses for these holdouts can therefore be compared with the predicted values of the holdouts derived from the model. A high association between the actual values and the predicted values establishes a high reliability and thus validates the model.
Simulation refers to the process when the derived model is used to estimate the preference share. The following are the three purposes of a discrete choice model in simulating the impact of a change of attributes:
1) Determining which attribute level or a combination of the levels contribute most to respondents’ choice of that drug and thus the preference share of the drug. Deriving the relative importance of attributes. For instance, to what extent a change of the price from $10.00 to $15.00 and/or side effects from high to low for drug A will affect the preference share of drug A. Does the efficacy have more influence on prescribing than other attributes tested? How important is formulary status relative to other attributes tested?
2) Assessing the cross-effects of attributes. As we indicated earlier, the unique feature in discrete choice is the estimate of cross-effects, such as brand by price. Therefore, the study of price elasticity is a very common application of discrete choice.
3) Examining the extent that one drug’s share increase/decrease may have influenced other competitors by each segment of the market. For instance, in treating patients with headache, will primary care physicians’ choice of Drug A be more influenced by its formulary than pain specialists? And, which competitors are most likely to draw share from or to lose share to?
Limitations
One of the limitations in discrete choice modeling is what is called the independence from irrelevant alternatives (IIA) assumption. This assumption is one of the properties underlying the multinomial logic models (Moshe Ben-Akiva and Steven R. Lerman, 1985). IIA assumption means that the ratio of the probabilities of choosing one alternative over another is unaffected by the presence or absence of any additional alternatives in the choice set. This is also called the “red bus/blue bus” problem. The IIA assumption means that the probability of choosing the red bus over the train is unchanged whether there is a blue bus in the choice set or not. On presenting a set of alternatives to physicians (e.g., Drug A, Drug B and Drug C), the IIA assumption means that physicians’ choice of an individual drug (e.g., Drug A) over another drug (e.g., Drug B) is independent of any other alternatives in the set (e.g., Drug C). In some situations, the products in a choice set are related. For example, generics and the original brand name drugs have the same chemical molecule and have similar characteristics. Choice of the brand name drug over other brand name drugs may be affected by the presence or absence of generics in the choice set. In such situations, IIA assumption is violated and some of the products in the choice set are related. Nested logit models, also referred to as hierarchical logit models, are used to accommodate the violation of the IIA property by allowing some of the alternatives to be related to each other. For more discussions on nested logit, please refer to the book Stated Choice Methods, Analysis and Applications (Louviere, Hensher, and Swait, 2000).
When situational variables are included in the choice task, we often have physicians repeatedly make prescribing choices for each of the situations. Therefore we have multiple responses from the same respondent. The choices made by same respondent are correlated. Mixed logit models (Revelt and Train, 1998, Brownstone and Train, 1999) are a way to explicitly account for correlations in unobserved utility over repeated choices by each respondent.
Because a discrete choice study uses multinomial logit models to estimate the attribute levels’ impact on product choices, it is traditionally estimated at the group or aggregate level. Conjoint, on the other hand, is estimated on an individual level so that the respondents can be classified based on individual utilities (e.g., through cluster analysis).
Individual utilities are critical for segmentation of respondents, which is an important component of product marketing. Recent developments in mixed logit (Revelt and Train, 1999) and hierarchical Bayes (Sawtooth Software, 1999) provide ways to estimate individual level utilities using very different approaches. Huber and Train (Huber and Train, 2000) found that the two approaches result in virtually equivalent conditional estimates for individual utilities.
References
Brownstone D. and Train K. “Forecasting New Product Penetration with Flexible Substitution Patterns.” Journal of Econometrics 89: 109-129, 1999.
Fishbein, M. A Behavior Theory Approach to the Relations Between Beliefs about an Object and the Attitude towards the Object. In M. Fishbein (Ed.) Readings In Attitude Theory and Measurement. New York: John Wiley & Sons, 1967, 389-399.
Green P.E. and Srinivasan. “Conjoint Analysis in Consumer Research: Issues and Outlook.” Journal of Consumer Research. 1978; 5(September): 103-123.
Green, P.E. and Wind, Y. Multiattribute Decisions in Marketing: A Measurement Approach. Hillsdale, III.: Dryden Press, 1973.
Huber and Train. “On the Similarity of Classical and Bayesian Estimates of Individual Mean Partworths,” working paper, Department of Economics, University of California, Berkeley, 2000.
Kuhfeld W.F. Marketing Research Methods in the SAS System. Version 8 Edition, January 1, 2000.
Louviere J.J. “Consumer Choice Models and the Design and Analysis of Choice Experiments.” Tutorial presented at the American Marketing Association Advanced Research Technique Forum, 1991.
Louviere J.J. “Analyzing Decision Making, Metric Conjoint Analysis.” Sage University Papers, Beverly Hills: Sage 1988.
Louviere J.J. Hensher D.A. and Swait JD. Stated Choice Methods, Analysis and Applications. Cambridge University Press, 2000.
Miller G.A. “The Magic Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information.” The Psychological Review, 1956.
Moshe Ben-Akiva and Steven R. Lerman. Discrete Choice Analysis: Theory and Applications to Travel Demand, The MIT Press, 1985.
Revelt D. and Train K. “Mixed Logit with Repeated Choices: Households’ Choices of Appliance Efficiency Level,” The Review of Economics and Statistics, 1998.
Revelt and Train. “Customer-Specific Taste Parameters and Mixed Logit,” working paper, Department of Economics, University of California, Berkeley, 1999.
Rosenberg, M.J. “Cognitive structure and attitudinal affect.” Journal of Abnormal and Social Psychology; 1956; 53:367-372.
Sawtooth Software Inc., CBC User Manual, Version 2.0 Sawtooth Software Inc., 2000. www.sawtoothsoftware.inc.
Sawtooth Software Inc., The CBC/HB Module for Hierarchical Bayes Estimation, 1999. www.sawtoothsoftware.inc.
Train K. Qualitative Choice Analysis. Cambridge, Mass.: MIT Press, 1986.