Editor’s note: Tim Glowa and Sean Lawson are partners in North Country Research, Calgary, Alberta. This article is based on a presentation by Tim Glowa to the Sixth Annual International Air Transport Association Market Research Conference in Geneva, Switzerland on December 8, 1998.
Consumer behavioral models provide a quantitative measure of the relative importance of one attribute as opposed to another. The most direct method of determining this importance is simply to ask people what is most important. The problem is that most respondents will simply mention that everything is important. Researchers saw the need to infer the relative importance of various attributes.
A very popular tool for modeling consumer behavior, since its appearance around 1970, is conjoint analysis. This tool, despite its widespread popularity, should not be used because of several critical assumptions inherent in its design which lead to faulty predictions. Discrete choice modeling was created to combat the deficiencies associated with traditional conjoint.
After reviewing the history of choice experiments, this article compares choice models with traditional conjoint analysis.
Where do choice experiments come from?
Choice experiments have a long and distinguished tradition, beginning with Louis L. Thurstone’s 1927 paper in Psychological Review on paired (comparison) choice experiments. Present interest in choice experiments derives from three major breakthroughs in theory and methods, which have occurred since the mid-1970’s:
1. Random utility theory (RUT) and multiple choice models.
Although Thurstone originally proposed what has come to be known as random utility theory (RUT), he was unable to extend it to the case of choices among more than two alternatives, such as three or more brands, vacation destinations, transport modes, etc. The key extension, which has lead to the widespread adoption and application of multiple choice models, is attributable to Dan McFadden, who extended Thurstone’s ideas in a seminal 1974 paper in “Frontiers in Econometrics,” edited by Zarembka. In this and subsequent papers, McFadden and others extend the basic theoretical ideas and show how they can be applied to a plethora of practical problems. In marketing and strategic research, multiple choice models have been applied to a very wide range of practical problems in which the choices of various customer groups are modeled as a function of a variety of marketing mix actions and differences in the individuals or groups making the choices.
2. Random utility theory-based choice experiments.
Until the work of Jordan Louviere, RUT-based choice models had been applied to analyze choices that could be observed in real markets, such as scanner panel choice data, observations of what customers chose reported in surveys, etc. Naturally, one cannot rely on such data for many strategic research problems, because of the following types of problems that frequently arise in real applications:
a) Forecasting demand for new, or category-revolutionizing products.
b) Forecasting demand for products in categories in which new and different attributes which were not previously a consideration in choice are introduced.
c) Forecasting demand for products in categories in which attribute ranges are stretched well beyond those in present markets.
d) Forecasting demand in markets in which serious multicollinearity is present among the predictor variables.
Louviere’s research, since extended by him and others, focused on developing statistical design technology to systematically and independently vary predictor variables of interest in a manner consistent with RUT and various multiple choice models derived from RUT.
The major advantage of this technology is that the strategic researcher is freed from the tyranny of real markets which are subject to market forces and constraints of technology. That is, the researcher can extend existing markets and even develop radically new markets by using principles from the design of statistical experiments to create markets offering products that do not now exist, products with attributes and/or attribute levels which do not now exist, and products whose attributes behave in statistically useful, non-collinear ways regardless of the existing pattern of collinearity in real markets.
3. Re-scaling of RUT-based multiple choice models
Ben-Akiva and Morikawa (1990, Transportation Research) and Swait and Louviere (1993, Journal of Marketing Research) showed that RUT predicted that a simple relationship existed between multiple choice models derived from choice experiments and multiple choice models derived from choices observed in real markets.
Since that time, a growing number of published papers have consistently verified the relationship, and affirmed the practical significance of the result: Choice models derived from experiments can be easily and theoretically consistently “re-scaled” to predict real market choices.
What is a choice experiment, and how does it differ from conjoint?
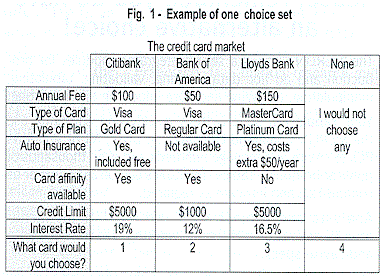
A choice experiment consists of two or more alternatives from which a target group of respondents are asked to choose, such as brands competing in a category or services such as airlines competing on the same city pair route. The choice alternatives are organized into sets called choice sets and each choice set presents either different subsets of competitors, different descriptions of competitors vis-a-vis their attributes or features, or both (see Fig. 1). In a typical choice experiment, each respondent will complete between six and twelve of these systematically generated cards.
 |
Thus, a choice experiment involves the design of alternatives and choice sets in which the alternatives appear. There are numerous ways to design such experiments, and as academic and practical interest continues to increase in choice experiments, the number of ways to design the experiments and the types of applications is growing rapidly.
Choice experiments differ from traditional conjoint analysis in many ways, despite the fact that many marketing researchers call choice experiments “choice-based conjoint,” while other researchers try to position traditional conjoint analysis as choice experiments, and yet others try to pass off a variety of techniques completely unrelated to choice experiments as choice experiments!
In particular, traditional conjoint analysis is based on linear models, such as ordinary least-squares (OLS) regression or ANOVA models. In a traditional conjoint analysis experiment therefore, the objective is to design a set of product descriptions called “profiles,” which are combinations of levels of a set of attributes being varied by the researcher (see Fig. 2). Notice that no mention has been made of “choice sets” in which profiles or brands compete with one another for customer’s choices. This is because traditional conjoint analysis profiles do not compete; rather, respondents from a target market express degrees of preference for each profile independently of other profiles. A single model which describes how preferences vary as a function of changes in attribute levels is derived for each respondent. Choices are simulated by assuming that each individual will choose that profile in a set of competing profiles that receives the highest predicted preference value.
 |
In this sterile, unrealistic, profile evaluation environment customers cannot indicate that they would prefer not to choose any of the profiles. Of course, it is a feature of real markets that few customers always choose those consistently what they express preferences. In fact, we know that customers choices often vary, and that preferences can be quite inconsistent with choices. For example, you may prefer BMWs to Hondas, but choose a Honda because you cannot afford a BMW. As well, choices often vary due to a variety of things that cannot be observed and anticipated, such as a change in one’s transport mode to commute to work due to weather, accidents, problems at home, etc. Thus, viewed from the researcher’s view, choices must have a random element.
This random element of choice behavior in real markets is the principal focus of RUT (and from which RUT derives its name). That is, preferences, or “utilities” from an economic point of view, are inherently unobservable because they are in customers’ minds. Choice experiments allow researchers to observe systematic variations in customer choices related to systematic variation in alternatives offered, attributes of alternatives, or both. Naturally, because choice behavior always contains a random element, researchers cannot perfectly explain choices. This “unexplained variation” in choice constitutes the random element.
Unfortunately, in traditional conjoint analysis no allowance is made for a random element in preferences or choices. Indeed, this is a rather glaring logical inconsistency insofar as conjoint analysts a) use a method to model customers’ preferences which assumes a random element in preferences, but then b) use the resulting model to predict choices as if there were no random element. That is, choices predicted by traditional conjoint choice simulators are deterministic and make no allowance for random error in choices.
Real customers who make choices in real markets frequently decide not to choose. That is, for whatever reason, some customers choose to delay purchases or choose no products offered in a particular category. Examples of the former customers include millions of potential customers for PCs who know they eventually want to have one at home, but are waiting either for prices to drop further, or functionality to increase, or both. Examples of the latter customers include those who are allergic to chocolate, and hence, will not buy chocolate products regardless of the category in which they are offered.
Unfortunately, traditional conjoint analysis focuses only on preferences for profiles; and there is no theoretically acceptable way to accommodate a preference for “non-choice.” Thus, even if a theoretically correct way were found to accommodate randomness in traditional conjoint preference models, there remains the problem of predicting non-choice. The logical consequence of limitation is that traditional conjoint analysis deterministically predicts the number of customers in a sample who are expected to choose a particular alternative given that they will choose an alternative.
The latter prediction is clearly of managerial interest, but accurate prediction requires a theory that takes randomness in choice into account, which traditional conjoint analysis does not. Furthermore, traditional conjoint analysts try to approximate this probability by rigorous pre-screening of customers to be sampled, which again represents a logical inconsistency insofar as this assumes knowledge or theory to determine explicitly which customers are in the target market of interest now, as well as which customers ever will choose a product in the target market. The choice experiment approach eliminates this logical inconsistency by allowing researchers to separate non-choice into as many strategically interesting sub-choices as required. For example, if one simply wants to know who will choose now, who will delay and who will never choose, choice experiment outcomes can be framed as a) choosing one of the offered alternatives, b) choosing to eventually choose but not given the set offered, or c) choosing never to choose regardless of what is offered.
Another feature of real markets is that products or services can compete across manager-nominated categories, or even within the same category, different products may offer different attributes or different levels of the same attributes. Traditional conjoint analysis can deal with such issues only at the cost of considerable increases in the complexity of the experimental designs used to study preferences.
Conclusions
Despite its widespread popularity, conjoint analysis is riddled with logical inconsistencies that undermine the credibility of its predictive capabilities by modeling an unrealistic environment. Problems associated with conjoint analysis include:
a) Conjoint experiments present respondents with an unrealistic environment where they are expected to indicate preferences for a product or service without competition. Although most other market research applications also have some degree of artificiality, research should endeavor to define the most realistic experiments as possible.
b) Conjoint experiments do not allow respondents to say they “would not purchase” given a set of attributes. This forced choice environment is completely unrealistic.
c) Choices predicted by traditional conjoint choice simulators are deterministic and make no allowance for random error in choices.
Fortunately for researchers, discrete choice modeling addresses all of the deficiencies associated with traditional conjoint analysis. By providing a more realistic choice experiment, discrete choice removes much of the uncertainty associated with traditional conjoint, and results in a more usable, predictive model.
References for further reading
Dick R. Wittink and Philippe Cattin, “Commercial Use of Conjoint Analysis: An Update,” Journal of Marketing, 53(3), 1989, pp. 91-96.
Paul Greene and V. Srinivasan, “Conjoint Analysis in Consumer Research: Issues and Outlook,” Journal of Consumer Research, 5, September 1978 pp. 103-123.
Paul Greene, “On the Design of Choice Experiments Involving Multi-factor Alternatives,” Journal of Consumer Research, 1, September 1974, pp. 61-68.
Louis L. Thurstone “A law of comparative judgment,” Psychological Review, 1927, 34: pp. 273-286.
Dan McFadden, “Conditional logit analysis of qualitative choice behavior,” pp. 105-142 in P. Zarembka (ed.) in Frontiers in Econometrics, New York: Academic Press.
Ben-Akiva and Morikawa (1990, Transportation Research) and Swait and Louviere (1993, Journal of Marketing Research)
Jordan Louviere, “Analyzing Decision Making: Metric Conjoint Analysis,” (1988), Sage University Papers Series on Quantitative Applications in the Social Sciences, No 67. Newbury Park, Calif.: Sage Publications.
Joffre Swait and Jordan Louviere, “The Role of the scale parameter in the estimation and the use of multinomial logit models,” Journal of Marketing Research, 1993, 30: 305-314.
Steven Struhl, “Discrete Choice Modeling: Understanding a better conjoint than conjoint,” Quirk’s Marketing Research Review, June 1994, Article 86.