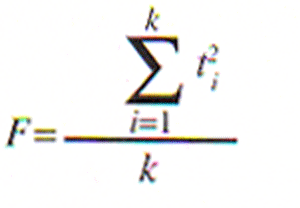Editor's note: The focus of this month's Data Use is a response to Gary Mullet's article "Regression regression," which appeared in the October 1994 issue of QMRR. The response, written by Albert Madansky, professor of Business Administration, and director, Center for International Business Education and Research at the University of Chicago, takes issue with some points made in Mullet's article. Following Madansky's comments is Mullet's response.
In his article, "Regression, regression" (October 1994 QMRR), Gary Mullet offers an explanation as to why an F-test in a regression shows that the regression is significant, yet no t-test associated with the individual regression coefficients shows up as significant. He points out that this is caused by the existence of correlation between the independent variable. This is the most commonly given explanation for the occurrence of this phenomenon (see, for example, pages 146-7 of Chatterjee and Price's "Regression Analysis By Example," 1977, John Wiley & Sons).
Unfortunately, the example that Mullet cites, in which there are two independent variables, temperature in Fahrenheit and temperature in Celsius, is a misleading, indeed incorrect, example of such a phenomenon. If temperature in Fahrenheit (X1) and temperature in Celsius (x²) are both measured correctly. then X1= 1.8 X2 +32, are multicollinear, and no regression package worth its salt would accept both these variables as independent variables in a regression. (In Mullet's words, the computer would give us nasty messages.)
It is also true that if X1 and X2 are measured with error the situation envisaged by Mullet - and the errors are uncorrelated with the true values or each other and have a as their expected values, then the self-same nasty messages will be forthcoming from the computer. The observed variables may not bear the precise relationship we all learned in high school, but their correlation will still be 1. We will still have multicollinearity and thus an invalid regression, not one which produces a significant F and insignificant t's as output.
Unfortunately, multicollinearity is not the only explanation of the significant F/insignificant t's phenomenon. To see this, let me first cite a mathematical relationship between the t-tests and the F-test. Suppose we have k independent variables in a regression, and assume for simplicity that each of the variables (the dependent as well as the independent variables) is measured from its sample mean, so that the regression intercept will be O. Assume also that the independent variables are orthogonal, i.e., totally uncorrelated with each other, so that there isn't the faintest hint of multicollinearity. Under these circumstances

that is, the F-test statistic (which tests whether the regression as a whole is significant) is equal to the average of the squares of each of the t statistics (which test whether a particular regression coefficient is significantly different from 0).
Now suppose the t-test degrees of freedom is 12 and we have two independent variables (i.e., k=2). Suppose also that all our tests are conducted at the 5 percent level of significance. Then the cutoff value for the F-test is the 95 percent point of the F distribution with 2 and 12 degrees of freedom, namely 3.89. Meanwhile, the cutoff value for each of the t-tests is the two-tailed 95 percent point of the t distribution with 12 degrees of freedom, namely 2.179. If each of our observed t values were 1.98, we would conclude that neither coefficient was significant. Yet the resulting value of the F statistic would be 3.92, and so we would conclude that we had a significant regression.
What's really going on here? Simply stated, the F-test addresses whether all the regression coefficients are 0; the t-tests address individually whether each regression coefficient is 0. Each of k regression coefficients may not be discernibly different from 0, but en toto the regression does significantly explain some of the variation in the dependent variable.
We can also ask the flip side of the question asked by Mullet, namely can one have a regression with a significant t-test but an insignificant F-test? The answer is yes, for a different reason. The F-test and t-tests are set at a significance level of 5 percent, so that the probability is .05 that we reject the null hypothesis when it is true. What is the null hypothesis? For the F-test it is that all the regression coefficients are 0; for each t-test it is that a particular regression coefficient is 0. Thus the null hypothesis for the F-test is the union of the null hypotheses of the individual t-tests. The probability associated with each t-test of accepting the null hypothesis when it is true is .95. If each of the t-tests is independent of the others, then the probability of accepting the hypothesis that all the regression coefficients are a via t-tests when that is in fact the case is .95k, not .95. When k=2, .952 = .9025, so that the implied level of significance based on using the t-tests to test whether all the regression coefficients are equal to a is .0975, not .05.
Ifk=20 we will on average reject a null hypothesis once when it is true; thus on average looking at 20 t-tests in a 20 independent variable regression you will state that one of the coefficients is significantly different from 0 when in fact it is not. The true significance level is 1_.9520 = .64, not .05. The F-test, though, retains its .05 probability of rejecting the hypothesis that all the regression coefficients are 0 when that hypothesis is true.
-Albert Madansky
Gary Mullet's response:
Madansky points out an alternative explanation why an overall F-statistic for the entire regression model may be significant and yet none of the t-statistics (F -statistics in some computer packages) for individual partial regression coefficients is significant at the same significance level. The major thrust of my original paper was to indicate that, yes, this can occur and, yes, it is frequently disconcerting to the analyst when it does.
The temperature example which I used is certainly not one which anyone would actually attempt to replicate. I doubt if anyone would seriously try to run a regression model using temperature measured in both Fahrenheit and Celsius as two separate potential explanatory variables. My discussion was more to generate an, "Ah, ha! I get it!" than to suggest using such highly correlated variables. However, and maybe this is more a function of my age than anything else, I recall running some regression analyses on a UNIVAC 1108 where I had messed up the data format card (yes, the term "card image data" alludes to the fact that data sets were once punched on actual cards and entered into the computer via a card reader) and all values of the dependent and all independent variables were read in as "0". The regression duly ran and the output showed no error messages, merely values of 0.00 for everything, including ratios of 0/0, except the adjusted R² was -.700. It seems like only yesterday that that happened, but it was more than a few years ago.
In Madansky's last paragraph, the reader needs to be aware that the reference is still to 20 orthogonal independent variables, not just any 20 "independent" variables, in the computation of the .64 significance level. This, too, points out the problem with the term "independent variable" in regression analysis in general,
Overall, I'm pleased that such issues are not just a worry of mine, but concern many others in the research industry as well.