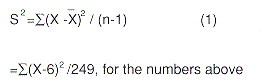Editor's note: Gary M. Mullet is a visiting professor in the Management College at Georgia Institute of Technology. His previous marketing research experience includes several years with Sophisticated Data Research and Burke Marketing Research. He has also taught at the University of Michigan and the University of Cincinnati. A reformed theoretical statistician, he is the author of several articles on statistics as applied to marketing research and is an active presenter at meetings of various professional societies.
Most of us have learned a lesson that bears repeating, especially since we just celebrated Valentine's Day a few months ago: Don't take your significant other for granted. An equally important lesson-which some have yet to learn-is: Don't take your data tabulation package for granted.
While Dear Abby, Dear Ann, and Dr. Ruth can help us with the former lesson, the example below, which shows why our data tabulations are not always what they seem to be, should help with the latter.
In what follows, I won't be talking about straight data tabulation-vanilla tab, as it's known to some. Most tab packages perform equally well on such tasks. However, frequently analysts require weighting or pooling of a particular group of banner points. It's here that taking our tab package for granted may cause problems.
The problem
Here's what happened. While looking at some tabs recently (and I don't even know what the tab package was, so I can't say if the one you use is guilty), three particular banner points were of interest-"Brand A," "Brand B," and "Brand A & Brand B." In other words, tabs were requested for Brand A, alone, Brand B, alone (these were independent cells), and, in this case at least, the combination of Brand A and Brand B. That is, the last banner point was to consider the two sets of brand information as if they came from a single sample of 250 respondents. The usual statistics were asked for-mean, variance, and standard error-and the results are shown below.
Table 1
| | Brand A | Brand B | Brand A & Brand B |
| n | 100 | 150 | 250 |
| Mean | 4.5 | 7.0 | 5.75 |
| Variance | 13.067 | 15.467 | 14.267 |
| Standard Deviation | 3.615 | 3.933 | 3.774 |
| Standard Error | .361 | .321 | .341 |
Brands A and B were not the only two considered in the survey. Thus, the "Brand A & Brand B" column is not the same as the total column, which usually is shown first in the tabulation. Instead, it was a specially created banner point, created with a specific purpose by the analyst.
It's pretty plain what was done. The two cell sizes were merely added to come up with the total of 250. For each of the other three statistics, a simple arithmetic mean was found. That is, the two values were merely added and divided by two, for each statistic on the table. The individual cell standard errors were correctly calculated by taking the square root of the variance divided by the cell size (or the standard deviation divided by the square root of the cell size).
If you recall back to when you first took basic statistics (or vice versa), you know that the standard error is used to either test the significance of the mean or for establishing confidence intervals. That's all right for either the "Brand A" column or "Brand B" column alone; for the combined or pooled column, with the exception of the sample size, every number is incorrect. Thus, not only is the mean wrong, so are any inferences based on this mean using the printed standard error. (The mean would be O.K. if the two cell sizes were the same; the other numbers are still incorrect.)
It's also interesting that no one questioned the above table; the rationale for accepting it at face value was that if a computer printed it, it must be correct. Simple algebra would confirm that either the combined variance is incorrect or the combined standard deviation must be (or both, as is the case). Since the standard deviation is the square root of the variance, we can't generally find numbers such that if we add them and divide the sum by two and then take the square root (the pooled variance converted into a standard deviation), we'll get the same result as if we take the square roots first, then add and divide by two (the pooled standard deviation). This comes from basic algebra, and common sense, not statistics.
First, we'll see what the correct numbers should be. Then we'll show just enough theory and formulae to see why they aren't correct as is. The correct numbers for the combined column are:
Table 2
| | Brand A & Brand B |
| n | 250 |
| Mean | 6.00 |
| Variance | ? |
| Standard Deviation | ? |
| Standard Error | ? |
Why all the uncertainty? Because the weighted mean is the only number that can be accurately computed from the statistics given for the original two banner points shown, i.e., Brand A and Brand B. It comes from taking each sample size times its respective mean and dividing the total by the new total sample size. That is:
[100(4.5) + 150(7.0)]/250 = (450 + 1050)/250 =1500/250 = 6
In other words, the sample mean rating for all 250 of the observations combined is 6.00. Intuitively, this is appealing, since the Brand A folks contribute 450 to the total and the Brand B sample contributes another 1050. Thus the sample mean behaves well.
Now, as you also probably recall from your introductory statistics course, the sample variance is calculated by taking the squared difference between each individual observation and the sample mean, adding these all up and dividing by the sample size minus one. Specifically,
 |
See the problem? Without another pass through the data by the tab package, we cannot calculate the combined sample variance. The individual variances were calculated by using the above formula for each of Brand A and Brand B; the first time 4.5 was used for the sample mean and the second time 7.0 was. So far so good. But is there any way that we can get the variance for our total sample of 250 from the summary data shown? Probably not, unless we go through the data with our tabulation package again. Hence, we can't accurately determine the combined standard deviation or standard error, either.
To further emphasize the point, again consider two independent cells. The first shows a mean of 1 and a variance of 3. The second shows a mean of 11 and a variance of 3. Although intuition (and the tab package used for our original example) would say that the combined variance is also 3, a moment's reflection should convince you that it will be much larger than that. Why? Because the individual variances of three are found by taking squared deviations from the respective means of 1 and 11. The combined variance will have to be found by taking squared deviations from the new mean of 6, assuming equal cell sizes. Clearly, things don't add up if we merely average the variances. It is safe to say that the variance correctly calculated from the combined sample will be larger, possibly by several order of magnitude, than the "average variance."
Conclusion
We've seen that it's imperative for the analyst to know and understand what goes on inside the data tabulation package used when banner points are combined. Otherwise, you could be faced with an array of statistics which are incorrect and these, in turn, could lead to incorrect statistical conclusions from the data. This, in turn, can cause either a real loss of dollars or a significant opportunity cost.
Here the combination was relatively simple; the banner points were simply to be pooled into a combined sample. It gets more difficult to be sure that the tabulation is done correctly when weighted banner points are produced. Another layer of the onion is when sums or differences are to be found. Finally, although here we were involved with independent cells, clearly such is not always the case. Dependent cells require even more special handling.
The moral is: don't accept the printouts at face value; probe, dig, and probe some more into the underlying computations.