Editor’s note: Rajan Sambandam is vice president/research at The Response Center, a Fort Washington, Pa., research firm.
Asymmetrical relationships among variables in satisfaction research have been increasingly investigated in the last decade. However most of the work has been published in academic journals (such as Marketing Science and Journal of Marketing Research), which may not always be accessible to practical market researchers. The objective of this article is to both provide a simple introduction to this topic and add to the existing body of knowledge.
Before examining the question of asymmetry, we need to think about symmetry. Consider a regression analysis where overall satisfaction with a hotel was used as the dependent variable and the cleanliness of the room emerges as a key driver with a weight of 0.44. The implication here is that a unit improvement on the independent variable will result in a 0.44 unit improvement in overall satisfaction. Conversely, a unit decrease in the independent variable will result in a 0.44 unit decrease in overall satisfaction; this is a symmetrical relationship. If the independent variable is measured on, say, a 10-point scale, this result is true regardless of which scale point is considered. In other words, moving from nine to 10 will have the same impact as moving from one to two.
Is this a reflection of the method used or the underlying reality? First consider the method. Regression analysis as used in this example (and often in key driver analysis) is a linear method. The above symmetrical description is the only way of interpreting the results. Hence even if the underlying reality is different, the method will not allow us to see things differently. Is the underlying reality different?
One could consider this question both theoretically and empirically. The theoretical argument that the reality is different goes back several hundred years to Daniel Bernoulli. He put forward the idea that utility is inversely proportional to the quantity of goods possessed. That is, “If the satisfaction derived from each successive increase in wealth is smaller than the satisfaction derived from the previous increase in wealth, then the disutility caused by a loss will always exceed the positive utility provided by a gain of equal size” (see Bernstein 1996). This idea was further refined by Kahneman (2002 Nobel Prize winner in economics) and Tversky when they developed prospect theory to show that people weight losses more than gains of equal magnitude when changes are measured from a reference point.
Essentially, we are talking here about an asymmetric effect where the impact on the negative side happens to be larger than the impact on the positive side. Does this apply to satisfaction research and can it be demonstrated? (See Anderson and Mittal, 2000, for a review.)
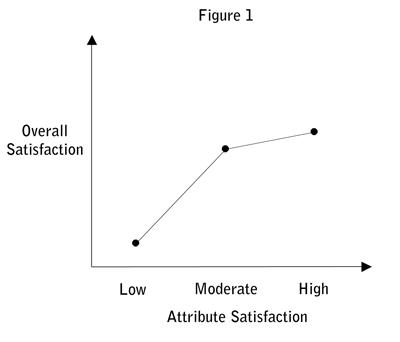
The simplest way to demonstrate asymmetry is to plot the relationship between an attribute and overall satisfaction (Figure 1). For simplicity, the attribute satisfaction scale has been divided into three parts (say, Dissatisfied, Moderately Satisfied and Very Satisfied). The kink or elbow in the chart shows the existence of an asymmetric relationship. The interpretation here is that moving respondents from the bottom boxes (Dissatisfied) to the middle boxes (Moderately Satisfied) has a stronger positive impact on overall satisfaction, than does moving them from the middle to the top boxes (Very Satisfied). Similarly, moving respondents from the middle to the bottom boxes has a stronger negative impact than does moving them from the top to the middle boxes.

Such an interpretation provides multiple courses of action for the manager. If the bottom boxes are more populated than they should be, then the strategy would be to try and move some people into the middle boxes. If the bottom boxes are sparsely populated but the middle boxes are heavy, then preventing the middle box people from migrating down would help immensely in maintaining the current overall satisfaction. Attributes of this type are often called “satisfaction maintaining”, but clearly the actual distribution will have to determine the recommended action.
Given the minimal gain in moving from the middle to the top boxes, it should be pursued only if it is inexpensive to do so. On the other hand, if maintaining a large number of customers in the top boxes is very expensive, some could be allowed to slide to the middle boxes without too much of a loss in overall satisfaction ratings. Comparisons with competitors can be very useful in understanding what types of improvements are possible.
The asymmetric relationship can also manifest as shown in Figure 2. In this case, moving respondents from the middle boxes to the top boxes has a much stronger impact than moving from the bottom to the middle boxes.

As we go through these options it is clear that the number of possible action recommendations increases quite a bit when the data are analyzed this way, as opposed to doing a regular regression analysis. If this were a completely linear relationship then both slopes would be equal (the line would be straight) and the recommendations would not be quite as nuanced.
Asymmetry in practice
Is it necessary to use only graphical or tabular methods to identify asymmetric relationships? Not at all - graphs and tables are just a simple way to do this. There are a few different ways of showing asymmetry using variations of regression analysis. Dummy variable regression is one such method. In this method, two coefficients are obtained for each variable, one pertaining to the upper part of the scale and the other to the lower part of the scale. Hence asymmetry analysis can be run with multiple independent variables.
The main problem with this approach is multicollinearity. While multicollinearity is a problem in regular regression, it is an even bigger problem in this type of analysis. One reason is that the automatic doubling of the number of variables (compared to a regular regression) increases the chances for collinearity. The second reason is that the two dummy variables that are formed from each variable are, by definition, highly correlated.
Multicollinearity’s deleterious impact can be seen by comparing the results of the multiple regression analysis to a series of simple regressions. If for example, the lower part of the scale has a stronger impact than the upper part in the simple regression and the opposite result is observed in the multiple regression, then we know that multicollinearity is having a strong impact. This is similar to checking the directionality of coefficients from a regular regression analysis against the correlation matrix, to see if multicollinearity is causing signs to reverse. Of course, multicollinearity could still have an impact without actually changing the signs of coefficients. This problem is even more pronounced when we run asymmetry analysis.
Hence the solution here may be to not use multiple regression to identify asymmetric effects. Multiple regression could be used to identify which set of variables truly drives the dependent variable. Then a series of simple dummy variable regressions could be used to identify the asymmetric impact of each key driver (if they exist). In this case, the asymmetry analysis serves as a “drill down” mechanism. Traditional key driver analysis identifies what is important and asymmetry analysis clarifies why it is important and how it should be acted upon.
Such an approach in the toothpaste market, for example, identified “whitening teeth” as a particularly interesting attribute. Its positive impact was more than twice that of its negative impact. Beyond that, the performance of the brand on this attribute clearly showed that there was room for improvement. Both the bottom and middle boxes were more populated than for other attributes and consequently the top boxes were more sparsely populated. Even when compared to other brands, the top boxes were less populated. Thus there was a clear opportunity for this brand to move people from the middle to the top boxes on this attribute and thus have a strong impact on purchase interest.
Up and down
While Figures 1 and 2 are representations of asymmetry in satisfaction, it can also be looked at as two symmetries joined together. Movement within the upper and lower part of the curve is symmetrical. Hence moving from say, the bottom to the middle and the middle to the bottom has exactly the same effect in terms of magnitude. It is only the sign that is different. Is it possible that there could be asymmetries within the upper and lower parts of the curve, as depicted in Figure 3? In other words, is it possible that moving from the top to the middle boxes has a different impact on overall satisfaction than moving from the middle to the top boxes?

The best way to show this may be with longitudinal data of a new product purchase where the attribute satisfaction ratings are likely to be in a transitory state due the newness of the product. Not having access to that kind of data, I used a cross-sectional proxy by utilizing data from two annual waves of a satisfaction tracking study. All items are measured on 10-point scales. The dependent variable was overall satisfaction while the independent variable was satisfaction with price (divided into Low, Moderate and High groups). Mean values of overall satisfaction were calculated for each of the three levels of price satisfaction in the two time periods.
In Table 1, M stands for mean overall satisfaction score while the subscripts H, M and L stand respectively for High, Medium and Low price satisfaction, with 1 and 2 indicating time period one and time period two. So for example, the mean overall satisfaction score for those who had high price satisfaction scores in time period one is 9.48 (MH1), while the corresponding score for those who had moderate price satisfaction scores in time period two is 8.31 (MM2). The absolute difference between the two scores is 1.17 (| MH1-MM2 |). The down arrow indicates that this difference is obtained when we go from high price satisfaction in one period to moderate satisfaction in the next.

In the second part of the table we see that going from moderate to high price satisfaction (represented by an up arrow) shows a difference of only 0.79. The same pattern of differences shows up when we look at the table corresponding to movement between moderate and low satisfaction boxes.
It appears that in both cases going from the higher level to the lower level (i.e., high to moderate or moderate to low) has a stronger impact on overall satisfaction than moving from the lower level to the higher level (low to moderate or moderate to high). What does this mean in practice? If over the course of time, the number of people slipping from top box rating to middle box rating is equal to the number moving from the middle to the top, the mean score on the variable may not change, but its impact on overall satisfaction could be adversely affected. As mentioned before, a better way of showing this would be with longitudinal data but the data used here certainly illustrate the complexities in the relationship that may not be apparent with a linear analysis.
Quite insightful
Asymmetry analysis can be quite insightful, especially in the area of customer satisfaction research. Its biggest advantage is that it can provide more precise recommendations for resource allocation than traditional key driver analysis. Generally speaking, key driver analysis results are provided using some variation of a quadrant chart - a comparison of importance and attribute performance that often focuses attention on the intersection of high importance and low performance. Asymmetry analysis takes this further by distinguishing between performance maintenance and performance improvement in key areas. This can be especially useful for the manager when finite resources need to be judiciously allocated.
References
Anderson, Eugene W. and Vikas Mittal. “Strengthening the Satisfaction-Profit Chain.” Journal of Service Research 3, Nov. 2000: 107-120.
Bernstein, Peter L. Against the Gods: The Remarkable Story of Risk. New York: John Wiley & Sons, 1996.
Kahneman, Daniel and Amos Tversky. “Prospect Theory: An Analysis of Decisions Under Risk.” Econometrica 47 (1979): 263-291.