Editor’s note: Ted D’Amico is a consultant to Erdos & Morgan, a Syosset, N.Y., research firm, and president of D’Amico Associates, a Jericho, N.Y., research firm.
In the vast majority of cases, demographic, psychographic and behavioral brand profiles are developed by identifying the characteristics and behaviors that are disproportionately possessed by a brand’s audience. Generally, a brand’s audience is said to disproportionately possess a characteristic or behavior if the audience’s index with respect to the characteristic or behavior is above a certain level (e.g., 120). Typically, the indices that are used in this brand profiling process are seen as if they are etched in stone - that is, they are viewed as population parameters without any margin of error. Additionally, in an attempt to determine a brand’s strengths and weaknesses, the brand’s index is generally compared on a measure-by-measure basis to the indices of other brands in the brand’s competitive set.
At first glance the above approach seems reasonable. However, on a closer inspection it is deeply flawed and can be severely criticized for: its use of indices to develop brand profiles; its failure to take into account the variability of these indices; its use of indices to determine a brand’s competitive strengths and weaknesses; and its sole focus on competitive set brands.
Let’s review each of these criticisms separately. Following this review, alternative approaches that circumvent these criticisms will be discussed.
The use of indices to develop brand profiles
In the present context, an index is a measure of propensity. That is, it tells you how much more or less a given segment (e.g., men 18-34) is likely to be part of a brand’s user group, or how much more or less likely a brand’s user group is to engage in a specific behavior (exercise regularly) or possess a specific characteristic (prefer to buy American). An index is usually derived by dividing the percent the segment or characteristic represents of the brand’s user group by the percent the segment or characteristic represents of the population under investigation. The result of this division is then multiplied by 100 to arrive at an index. Thus, if a segment has an index of 125, it means that the segment is 25 percent (125 - 100) more likely to be part of the brand’s user group than would be predicted based on the percent the segment represents in the population under investigation. Conversely, if a segment has an index of 75, it means that the segment is 25 percent (75 - 100) less likely to be part of the brand’s user group than would be predicted based on the percent the segment represents in the analytical population.
Although indices are typically used to develop brand profiles, they suffer from two major problems. The first is that the maximum index a segment can obtain is inversely related to the segment’s size within the population under investigation. That is, compared to a smaller segment, the maximum index that a larger segment can achieve is considerably smaller. For example, it is possible for African-Americans to obtain an index of 775 because they only represent approximately 12.9 percent of the U.S. population (100 percent/12.9 percent x 100 = 775). In contrast, the maximum index that Caucasians can achieve is 126 because they represent approximately 79.6 percent of the U.S. population (100 percent/79.6 percent x 100 = 126). Thus, if indices are used to assess the determinants of purchase, the importance of certain demographic, psychographic and behavioral characteristics will be severely overstated, while others will be severely understated.
The second major problem is that, when indices are used to profile brand audiences, the segments and behaviors that are often used to describe the brand often account for a relatively small percentage of brand users. This is because low-incidence segments and behaviors have a much greater likelihood than large incidence segments and behaviors to have high indices.
The failure to take into account the variability of indices
When analyzing any statistic derived from a sample, one should always determine the margin of error surrounding the statistic. This is particularly true for indices for low-incidence segments and behaviors. To illustrate this point, consider the following hypothetical example. In a syndicated study consisting of 10,000 adults, one percent used Product X, 100 people viewed Program A, 100 people viewed Program B, and the incidence of using Product X among Program A and Program B viewers was 1 percent and 2 percent, respectively. Thus, with respect to the usage of Product X, Program A has an index of 100 (1 percent/1 percent x 100) and Program B has an index of 200 (2 percent/1 percent x 100). Based on the comparison of the two indices, one would erroneously conclude that, among the adult population, Program B viewers are two times more likely to use Product X than are Program A viewers. However, if one examines the situation more carefully, one realizes that only one of the 100 Program A viewers used Product X, while two of the 100 Program B viewers used the same product. Thus, the difference in using Product X between the two programs is only 1 percentage point, which is not even significant at the 40 percent level of confidence (chi square = .338, df = 1, p = .56).
Using indices to determine a competitive brand’s strengths and weaknesses
The above example clearly illustrates the problem of using indices to determine a brand’s competitive strengths and weaknesses. As can be readily inferred from this example, the indices for low-incidence segments and behaviors can vary substantially, while the indices for high-incidence segments and behaviors can only vary within a limited or restricted range. For example, if the incidence for a given behavior in the population is 1 percent, the index for a given brand can vary from 0 to 10,000 (100 percent/1 percent x 100). In contrast, if the incidence for a given behavior in a population is 75 percent, the index for a given brand can vary from 0 to 133 (100 percent/75 percent x 100). Given the fact that indices can vary to a much greater degree for low-incidence segments and behaviors, brand differences with respect to indices should not be the metric used to determine a brand’s competitive strengths and weaknesses or the drivers (or correlates) of brand usage.
Focusing on competitive set brands
All too often when analyzing a brand’s competitive strengths and weaknesses, the analysis is restricted to only those brands within the brand’s competitive set. This is particularly true when the target brand is a media vehicle (e.g., magazine or newspaper). When I was working for an advertising agency, salesmen often showed me data for their publication and the data for 10 or fewer competing publications. The salesmen would often point out that their publication was first in its competitive set on a given measure in terms of its audience, index or CPM. My reply to these salesmen was that I was the fastest person in my competitive set, which consisted of me and everyone slower, and I was the smartest person in my competitive set which consisted of me and everyone “dumber.” My point in making these comments was not to be difficult but to point out to these salesmen that when making media choices, I am not restricted to publications in their competitive set. Such a parochial approach can not only lead to inefficient media buys but it can also paint an incorrect picture of a brand’s relative position within the marketplace.
Now that we have discussed the problems associated with traditional approaches for profiling brands and determining competitive strengths and weaknesses, it is time to discuss alternative approaches which circumvent these problems.
Use an incidence ratio
One way to circumvent the “uneven ceiling” problem associated with an index is to use an incidence ratio. This is because, with this statistic, the highest level that can be obtained is unlimited for each segment. The elimination of this ceiling effect is accomplished by dividing the incidence for segment members by the incidence for non-segment members. The result of this division is a likelihood (or odds) ratio that expresses how much more or less likely people within the segment are to use the brand relative to people who are not in the segment.
To illustrate the difference between indices and incidence ratios as they relate to a ceiling effect, consider athletic supporters, which are used exclusively by men. Because men represent 100 percent of the users for this product and they represent about 50 percent of the population, the maximum index for this segment is 200 (100 percent/50 percent x 100). In contrast, assuming that no women use athletic supporters (which hopefully is the case), the maximum incidence ratio for men is infinite because the incidence for men is divided by zero. It is important to keep in mind that the incidence ratio for a given segment could be infinite regardless of the segment’s incidence in the population. For example, if two products are used exclusively by men and, in the adult population, one has an incidence of use of 1 percent and the other has an incidence of use of 40 percent, both products have the same incidence ratio (infinity) among men because each incidence level is divided by zero, which represents the usage level of non-segment members (women). In contrast, in the above case, the lower-incidence product has an index of 10,000 (100 percent/1 percent x 100), while the higher-incidence product has an index of 250 (100 percent/40 percent x 100).
Phi correlation coefficient
For reasons stated previously, a brand’s audience profile should not be developed on the basis of indices. If indices are not to be used, however, what should be used? In developing profiles for a brand, one should generally find those segments and behaviors that account for a large portion of brand users and are positively related to brand usage. One statistic that generally fulfills these two requirements is the phi correlation coefficient. When applied to brand profiling, these coefficients tell you how well segment membership or engaging in a specific behavior predicts brand usage. For example, how does having an annual household income of $150,000 or more predict whether or not people use the brand? How well is brand usage predicted on the basis of whether people own a Ford, Lexus or a summer vacation home?
As alluded to above, one of the great advantages of a phi coefficient is that, in order for this statistic to be high for a given segment (or behavior), a large and disproportionate number of brand users must be segment members. Conversely, if a segment (or behavior) indexes high (or has a high incidence ratio) but accounts for a small percentage of total brand users, the phi coefficient for the segment will be relatively low. For example, in the United States, sickle cell anemia is a disease that occurs almost exclusively among African-Americans. However, only a very small percentage of African-Americans (less than one in 500) have sickle cell anemia. Consequently, if one tried to predict whether a person in the United States was an African-American on basis of the presence or absence of this condition, one would be wrong the vast majority of time because 499 out of every 500 African-Americans do not have sickle cell anemia. As can be readily seen from this example, the intelligent use of phi coefficients safeguards against selecting behaviors and segments that account for a disproportionately small number of brand users.
It should be noted that when you square a phi coefficient you produce a statistic called explained variance. In the present context, this statistic tells you what percent of the variance seen for brand usage is explained by segment membership. The advantage of using explained variance as a measure of predicting brand usage is that negative and positive phi coefficients are put on an equal footing. For example, if the phi coefficient for Segment A is +.6 and the phi coefficient for Segment B is -.6, the percent of explained variance in both cases is the same (36 percent), indicating that they are both equally strong predictors of brand usage.
Two approaches
Following is a discussion of two approaches that can be used to calculate a phi coefficient or its equivalent. The first approach is specifically designed for aggregate-level data; the second is specifically designed for individual respondent-level data. In either case the resulting statistics are identical, with each one telling you the relationship between segment membership and brand usage or ownership.
Aggregate-level data
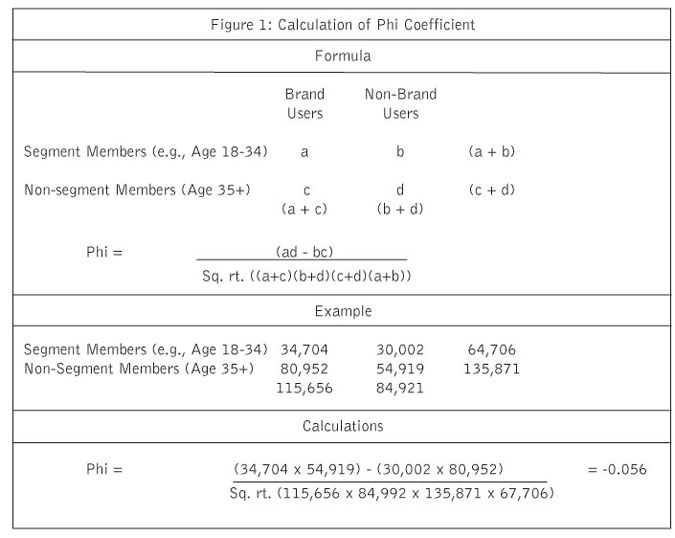
Figure 1 shows the formula and provides an example for calculating a phi coefficient when you are working with aggregate-level data. As can be seen by examining Figure 1, all that is required to calculate a phi coefficient is to construct a two-by-two matrix and enter the following information:
The number of segment members who use the brand is entered in Cell A
The number of segment members who do not use the brand is entered in Cell B
The number of non-segment members who use the brand is entered in Cell C
The number of non-segment members who do not use the brand is entered in Cell D

Once these data have been entered, simply follow these five steps:
Multiply the number of segment members who use the brand by the number of non-segment members who do not use the brand (Cell A x Cell D = 34,704 x 54,919 = 1,905,908,976).
Multiply the number of segment members who do not use the brand by the number of non-segment members who use the brand (Cell B x Cell C = 30,002 x 80,952=2,428,721,904).
Subtract the result from Step 2 from the result in Step 1 (1,905,908,976 - 2,428,721,904 = -522,812,928).
Multiply the sum of each of the two columns and each of the two rows and take the square root of the result. Square root of (64,706 x 135,871 x 115,656 x 84,921) = 9,292,387,168.
Divide the result from Step 3 by the result from Step 4 (-522,812,928/9,292,387,168) = -.056.
As mentioned previously, the equivalent of a phi coefficient can be calculated if you are working with respondent-level data. In this case, all you have to do is to dummy-code each respondent with respect to segment membership and brand usage and then compute a Pearson product-moment correlation coefficient.
As can be seen in Figure 2, dummy-coding boils down to using 0s and 1s to code both segment membership and brand usage. Specifically, respondents are assigned a segment code of 1 if they belong to the segment under investigation (males), and 0 if they do not (females). Similarly, respondents are assigned a usage code of 1 if they own a brand (Ford) and 0 if they do not. Once all respondents have been coded in this manner, a correlation coefficient is computed. This coefficient is then squared to determine the amount of variance accounted for by segment membership with respect to brand usage.

Respondent-level user data
When examining any media metric, one should always evaluate the reliability of the estimate, especially when dealing with indices. The best way to do this is to calculate the 95-percent confidence limits surrounding the audience estimate for the given measure and then use the upper and lower estimates for the measure to calculate low and high index estimates. The specific steps, formulas and calculations needed to be followed to accomplish this goal are shown in Figure 3.

As can be seen by examining Figure 3, the standard random sample formula for calculating the variability of an audience estimate (square root of pq/n) is used in the below example, except that the sample size is adjusted to take into account the statistical efficiency of the study’s sample, which in this case is 75 percent. The reason for doing this is because few if any syndicated media and marketing studies precisely reflect the analytical population. This is because certain segments are often oversampled and/or because certain segments respond at a higher or lower rate than what is expected. Consequently, the sample has to be weighted and sample balanced to known census data in order for it to be reflective of the population under investigation. These weighting and balancing procedures, however, reduce the statistical efficiency of the sample by a certain amount which has to be taken into account when calculating the variability surrounding audience estimates. Thus, if the sample size of a study is 20,000 and the study’s sample efficiency is 50 percent, then the study’s effective sample size is 10,000 (20,000 x 50 percent).
More appropriate way
As mentioned previously, comparing the indices of the target brand to the indices of competing brands can lead to very misleading conclusions about the target brand’s competitive strengths and weaknesses and the drivers of brand usage. A more appropriate way to determine competitive strengths and weaknesses and the drivers of brand usage is to calculate, on a measure-by-measure basis, the percentage difference in composition between the target brand and each competing brand. To illustrate why this is so, consider the following two examples.
Example 1
In the adult population, 50 percent use Product B. However, among those who own the target brand, 75 percent use Product B (index = 75 percent/50 percent x 100 = 150), while 50 percent who own Brand A use the product (index = 50 percent/50 x 100 = 100). Thus, in this example, the compositional difference between the two brands is 25 percentage points (75 percent - 50 percent), the target brand’s relative index versus Brand A is 150 (75 percent/50 percent x 100) and the index difference is 50 (150 - 100).
Example 2
In the adult population, 1 percent use Product C. However, among those who own the target brand, 2 percent use Product C (index = 2 percent/1 percent x 100 = 200), while 1 percent who own Brand A use the product (index = 1 percent/1 percent x 100 = 100). Thus, in this example, the compositional difference between the two brands is 1 percentage point (2 percent - 1 percent), the target brand’s relative index versus Brand A is 200 (2 percent/1 percent x 100), and the index difference is 100 (200 - 100).
As can be readily seen by comparing these two examples, if one used the relative index or the index difference approach to determine the target brand’s strengths and weaknesses and the correlates of brand usage, one would incorrectly conclude that usage of Product C is a stronger determinant of brand usage and represents a greater strength for the target brand.
Before discussing the alternatives to focusing on a competitive set for evaluating a brand’s performance in the marketplace, a few words are in order regarding other approaches or statistics that could be used to determine both a brand’s competitive strengths and weaknesses and the drivers of brand usage.
In both cases, either a chi-square statistic or a phi coefficient could be used. It should be noted, however, that if one rank-ordered the target brand’s strengths and weaknesses versus a given competing brand using either chi-square statistics or phi coefficients, the rank order of the target brand’s strengths and weaknesses would remain the same and would be identical to the ordering which would be obtained if one used compositional differences.
Two frames of reference
As stated previously, evaluating a brand’s performance solely in the context of its competitive set can paint an incorrect picture of a brand’s relative position within the marketplace and its relative competitive strengths and weaknesses. To circumvent these problems, one should have two frames of reference for interpreting a brand’s performance. The first should consist of all brands in the target’s competitive set, while the other should consist of all brands in the category.
When analyzing the target’s performance with respect to these two frames of reference, one should analyze the target’s relative performance with respect to audience size/coverage, composition/index and cost, as well as other factors such as loyalty, opportunity and vulnerability. One way to do this is to rank the target’s performance on each of these metrics with respect to all brands in its competitive set and with respect to all brands in the category.