Editor’s note: Tony Babinec has been with SPSS, Inc. for 10 years. He is currently a product manager responsible for the statistical content of the software as well as insuring that the software addresses the needs of application areas such as market research. He has a background in advanced statistics and survey research methods. He has written and presented numerous SPSS training courses, and is active at meetings of various professional associations.
Correspondence analysis is an emerging technique suitable for analyzing two-way tables. It is already available in a number of standalone microcomputer programs (see March, 1988 issue of Quirk's Marketing Research Review for a list) and will soon be available in popular comprehensive programs such as SPSS. This article will show some of the uses of the technique.
Traditional analysis of tabular data
In survey research and market research it is often the case that possible responses to variables represent categories rather than quantities or amounts. Examples of this are:
- The respondent is "male" or "female."
- A beer is "light" beer or a "dark" beer.
- A test product tastes "too sweet," "just right," or "not sweet enough."
- The respondent lives in "New England," "The Southeast," or "The Northwest."
Sometimes the categories of a variable have a natural ordering. In the Taste variable above, "just right" sits in the middle between "too sweet" and "not sweet enough." Such categories are ordered categories and the variable is said to be measured at the ordinal level. On the other hand, the categories of the above Region variable have no inherent ordering. Such categories are unordered categories and the variable is said to be measured at the nominal level. In either case, when coding responses prior to analysis, you typically represent the categories by sequential numbers (1,2,3,...). No strict numeric interpretation is attached to these codes. If a variable has ordered categories, you used ordered numbers to represent the categories in meaningful order. If an ordinal variable with three categories is scored 1, 2, and 3, it is not in general the ease that category 1 and category 2 are the same distance apart as category 2 and category 3.
Whether variables are measured at the nominal or ordinal level, the traditional analysis of such variables begins by looking at frequency distributions and follows with crosstabulation of variables taken two at a time. Assuming that you are working with a suitably drawn sample of data, you crosstabulate two variables and produce the chi-square statistic to test the usual hypothesis of no association. If the chi-square test of no association is significant, you reject the hypothesis of no association. You then characterize the association between the two variables using some measure of association. Measures such as Phi, Cramer's V, Lambda, or Goodman and Kruskal's Tau are appropriate when the variables being tabulated are measured at the nominal level, or when both variables in the analysis are not ordinal. If both variables are ordinal, then additional measures such as Kendall's Tau-b and Tau-c, Gamma, and Somers' D are available. Some researchers like to look at Pearson's r computed on ordinal variables. When doing so, Pearson's r is computed as if the scores on the two variables are literally the sequential numeric codes you use to represent the categories.
In any event, if the chi-square test of no association is significant, you attempt to characterize the association in the table with a measure of association consisting of a single number which somehow quantifies the association in the table. Some statisticians have objected to this, for in a many-celled table it can be argued that the detail in the table is sufficiently rich so that it defies easy summary in a single number. This realization has led to the development of other techniques. These include loglinear models, association models, and correspondence analysis.
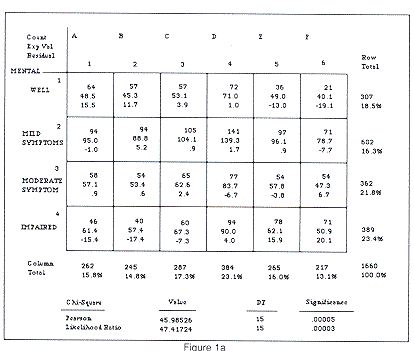
Let's look briefly at a traditional analysis of a famous two-way table: Srole's Midtown Manhattan data. These data were originally reported in 1962, and have been analyzed many times in different ways. Srole's data relates the mental health status of a respondent to his/her parents' socioeconomic status. Mental health status is one of four categories: "well," "mild symptoms," "moderate symptoms," and "impaired." Parental socioeconomic status is one of six categories ranging from "A" (high) to "F" (low). The sample size is 1660.
Figure 1a shows the crosstabulation of mental health status and parental socioeconomic status.
 |
The first cell value is the observed cell frequency, the second cell value is the expected cell frequency under the hypothesis of no association, and the third cell value is the residual or discrepancy between the observed and expected cell counts. The Pearson chi-square statistic, which is based on the discrepancies between observed and expected cell counts, has a value of 45.98 on 15 degrees of freedom, which is highly significant. Therefore, we reject the hypothesis of no association. Examination of the cell counts shows some evidence of a diagonal pattern, wherein high parental SES is associated with well mental health, and low parental SES is associated with impaired mental health.
Figure 1b shows the same crosstabulation with row percents.
 |
If mental health status and parental socioeconomic status had been statistically independent, then the row percents in any of the four rows would be identically equal to the marginal percents of the columns (15.8, 14.8,...13.1), also known as the average row profile. Because mental health status and parental socioeconomic status are dependent, the row percents or row profiles differ among each other as well as from the average row profile.
Figure 1c shows the same crosstabulation with column percents.
 |
Again, if mental health status and parental socioeconomic status had been statistically independent, then the column percents in any of the six columns would be identically equal to the marginal percents of the rows (18.5, 36.3, 21.8, and 23.4), also known as the average column profile. Because mental health status and parental socioeconomic status are dependent, the column percents or column profiles differ among each other as well as from the average column profile.
The dual concepts of discrepant row profiles or column profiles in a single table form the bridge to our introduction of correspondence analysis.
Correspondence analysis of tabular data
Correspondence analysis represents the row categories and/or column categories of a two-way table in a low-dimen-analysis in the family of techniques known to marketers as perceptual mapping, which includes other statistical techniques such as factor analysis, discriminant analysis, and multidimensional scaling. Examination of the plot produced by correspondence analysis reveals like and unlike categories within the variables as well as patterns of association between the variables in the two-way table.
To find the dimensionality associated with a particular table, compare the number of rows less one to the number of columns less one and take the minimum. For the Midtown Manhattan table, the minimum of 4-1 and 6-1 is 3. For large tables, the dimensionality needed to exactly represent the row and column categories may be a large number, but your hope is that a low-dimensional representation of the table shows most of what is going on in the table.
Figure 2a shows the dimensional analysis of the Midtown Manhattan data. This and the following output were produced by the ANACOR procedure, one of a number of new market research procedures currently undergoing development and testing at SPSS, Inc.
 |
The total inertia - equal to 0.0277 - is calculated as the chi-square value for the test of no association (45.98) divided by the table total (1660). Intuitively, the total inertia is a measure of the variance or discrepancy of the row profiles (recall Figure 1b, p.16) around the average row profile or of the column profiles (recall Figure 1c,) around the average column profile. Through a sophisticated mathematical-statistical tool known as singular value decomposition, correspondence analysis decomposes the total inertia of the table into pieces in an optimal way. The first piece explains as much of the total inertia as possible, the second piece explains as much of the remaining total inertia as possible and is independent of the first piece, and so on. For this reason, correspondence analysis is sometimes characterized as principal components analysis of nominal data. Figure 2a indicates that, overall, a two dimensional representation of the row and column categories should be a very good representation of the Srole data, for it accounts for 98.9% of the total inertia.
Another interpretation of correspondence analysis is in terms of scores it attaches to the row and column categories. In one step, correspondence analysis lets you do the following:
- Find a set of scores for the row categories which separates the row categories as much as possible.
- Find a set of scores for the column categories which separates the column categories as much as possible.
- Find a set of scores for the rows and a set of scores for the columns which are correlated as much as possible.
You can examine the row scores produced by correspondence analysis to find like and unlike categories on the row variable. Similarly, you can examine the column scores produced by correspondence analysis to find out like and unlike categories on the column variable. You can produce as many sets of these scores as there are dimensions, although it will be the first few dimensions' scores which are most important to an understanding of the data.
Figure 2b shows the optimal scores for the mental health status categories using a two-dimensional solution.
 |
The first dimension scores show the strong ordinality of the mental health status categories. That is, mental health status codes of 1 through 4 are monotonically related to the optimal scores, which are ordered from most negative to most positive. What is more, the scores for category 2 (mild symptoms) and category 3 (moderate symptoms) are very similar, suggesting the similarity in their row profiles (see Figure lb). Thus, you might conclude that group 1 is different from group 2 and 3 which in turn is different from group 4. The similarity of categories 2 and 3 suggests collapsing the categories and re?running the table. The second set of scores for mental health status suggests a contrast of the moderately impaired group with the others.
Figure 2c shows the optimal scores for the parental SES categories.
 |
The first dimension scores show that with the exception of category B, which is slightly more negative than category A, the categories of parental SES are otherwise in the "right" order. Categories A and B have almost the same score, as do categories C and D, suggesting possible ways of collapsing the parental SES categories.
Finally, Figure 2d shows the joint plot of the mental health status and parental SES categories.
 |
This plot tells pictorially what we learned through an examination of the row and column scores. Again, examination of this plot shows categories within the row variable and/or the column variable which are like and unlike. Moreover, you learn about the association between the variables, for the "well" category is juxtaposed near categories A and B of parental SES, the "impaired" category is juxtaposed near categories E and F of parental SES.
As several commentators have pointed out, it is legitimate to interpret distances among the categories of one variable, but care should be exercised in interpreting distances between categories of separate variables. You can interpret the relative position of one category of one variable with respect to all the points of the other set.
The asterisk in the plot represents the "center of gravity," that is, the average profiles of the row and column variables. Points near the center represent categories which are not discrepant from the average profile, while points far from the center represent discrepant categories.
One final comment: In the interest of brevity, we have omitted other portions of the output typically obtained when doing correspondence analysis. You can produce other statistics and measures not shown as aids to the interpretation of the axes of the plot and as indicators of the quality of representation of the row and column points in the low?dimensional space.
Uses of correspondence analysis
In sum, you can use correspondence analysis in any of the following situations:
- Quantify a qualitative variable. We often use sequential whole numbers to represent categories of a nominal or ordinal variable. Correspondence analysis produces optimal scores for the categories.
- Replace the codes on one or more variables with the optimal scores and use the resulting variables in further analysis.
- Find the maximal correlation between the row and column variable.
- Suggest like and unlike categories of the variables.
- Suggest which categories might be collapsible.
- Suggest nominality or ordinality of a variable.
- Works when your variables are dichotomous.
- Can be used to score "missing" or "nonresponse" categories. Consider a simple attitudinal item where 1 is "yes," 2 is "no," and 9 is "don't know. " If you include the 9 category in the analysis, it might obtain an optimal score which puts it between the "yes" and "no" category. Your scoring of the category as 9 would in that case have been misleading, or at least uninformative.
Conclusion
Correspondence analysis is restricted to the case when you have two categorical variables. If there are more than two variables of interest, there exist a number of ways of collapsing or re-expressing the data so that you end up with two variables to analyze. Moreover, correspondence analysis has been extended to the situation when there are more than two categorical variables. The resulting technique is commonly known as multiple correspondence analysis or homogeneity analysis.
Correspondence analysis has also been extended in another way. You might have a mix of variables measured at different levels - nominal, ordinal, and quantitative. The technique for analyzing variables with this mix of levels is nonlinear principal components analysis.
Taken together, this family of techniques represents an exciting set of analytic tools for the situations commonly faced by market researchers and survey analysts. These techniques accommodate a mix of levels of measurement, and produce intuitive plots which give insight into what's going on in your data. Their use should give you the edge in describing patterns in the data for your own edification as well as that of your client or boss.