Editor’s note: Yilian Yuan is director, marketing analytics, IMS Health, a Plymouth Meeting, Pa., health care information firm. Gang Xu is associate professor and project director, Jefferson Medical College of Thomas Jefferson University, Philadelphia.
Conjoint analysis is a technique that evaluates the importance of a product’s attributes to consumers. For a pharmaceutical product such as a drug, its attributes may include price, dosing, efficacy, and side effects, among others. Conjoint analysis is used to examine how consumers’ perceptions of these attributes influence their preference of the products. In a marketing research study for the pharmaceutical industry, “consumers” usually refers to physicians and patients. As we know, when consumers are making decisions on either prescribing a drug (e.g., physicians) or buying a drug (e.g., patients), they are comparing the drug with other drugs on the market. They are evaluating almost all the attributes of the drugs, the pros and cons, simultaneously. A drug may have a low price, but if it requires three daily dosages, it may be a less convenient option. Similarly, a drug with a high efficacy may also have many side effects. In this regard, consumers are making trade-offs: they set the priorities in terms of importance of these attributes to the patients. Consequently, their preference to a product depends on these priorities. One uniqueness of conjoint analysis is that it assesses a consumer’s preferences more accurately than other traditional methods by examining these trade-offs. For this reason, conjoint analysis studies are also sometimes referred to as a multi-attribute trade-off studies.
Conjoint analysis is perhaps the most widely used technique in quantitative marketing research. Since its first introduction in the early 1970s (Green and Rao, 1971; Green and Wind, 1975), it has been applied in many different areas ranging from cars (Johnson, 1974) to air travel (Green and Wind, 1975), job application (Norman 1980), the arts (Currium, 1981), health plans (Acito and Jain, 1980), and medicine (Graf et al, 1993). It is perhaps the most documented applied statistical techniques in quantitative marketing research (Louviere, 1988).
Practically, a conjoint study answers the following three key research questions:
1. How important are a product’s attributes to consumers? In a pharmaceutical marketing research study, for instance, we ask how physicians perceive drug X’s attributes such as efficacy, dosing, and cost. The feedback provided by physicians can be used in concept testing, designing clinical protocols, making marketing decisions and enhancing marketing efforts.
2. What profile, or combination of attributes, is deemed most attractive to consumers? In a pharmaceutical marketing research study, for instance, the question would be: Do physicians consider a drug with fewer side effects, lower efficacy, higher cost, and more difficulty of administering more attractive than a drug with more side effects, higher efficacy, lower cost and ease of administration?
3. What is the share of preference for the new product? For instance, a pharmaceutical company intends to introduce a new drug in an already crowded therapeutic area. It wants to assess how the new drug will perform in comparison with the existing drugs and how share of preference of the existing drug changes as a result of the launch of the new drug.
Design
The design is the first and crucial step in developing and implementing a conjoint study. In this article, we’ll focus on the general perspectives of the design rather than elaborate on the details of the design issues. (See Kuhfeld, et al., 1994 for more discussion on this issue.) There are largely three steps in designing a conjoint study: (1) determine the number of attributes and attribute levels; (2) determine the number of profiles; and (3) calculate the sample size.
1. Determine the number of attributes and attribute levels
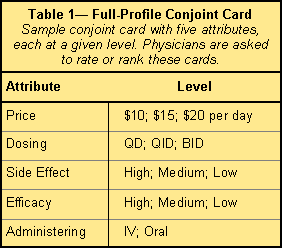
For evaluating a product, the first thing is to decide the number of attributes and levels of each attribute. A level here refers to the value of the attribute. For instance, an attribute of “price” could have three levels: $10 per day, $15 per day and $20 per day. Table 1 shows a profile of conjoint card with five attributes.
 |
A common approach to selecting attributes and attribute levels is through a focus group. For a conjoint study in the pharmaceutical industry, a focus group usually consists of a panel of experts in the study areas or consumers of products (e.g., physicians or patients) from whom the list of attributes and attribute levels are elicited. This phase of qualitative marketing research is crucial not only for generating the appropriate list of attributes and attribute levels, but also for helping determine whether a sufficient amount of information has been included so that physicians or patients can respond to the profiles in a meaningful way.
The guideline for selecting attribute and attribute levels is straightforward: They must be unambiguous and actionable. In other words, they should be clear and precise in expression and meaning, and can be implemented in practice and reality. Unimportant attributes and unrealistic attribute levels should be identified and eliminated with caution.
2. Determine the number of profiles
Before we determine the number of profiles, let’s first briefly review the concept of full-profile design.
Full-profile design
Once the attributes and attribute levels have been determined, we start to generate a variety of combinations of the attribute levels, each different from another. For instance, for an attribute of “price” with three levels ($10, $15 and $20) and an attribute of dosing with three levels (BID, QID, and QD), we have a total number of nine combinations (32=9: the base is the number of levels and the exponent is the number of attributes). In a conjoint study, each of the combinations is named “profile” (also termed “task” or “run”) and thus a design including all combinations is called full factorial design. For four attributes with three levels each and additional one attribute of two levels, we have a total of full-factorial 162 profiles (34 x 21 = 162). In a full factorial design, all main effects of attributes and the interactions among them can be estimated.
In a typical conjoint analysis, a consumer (e.g., a physician) is asked to rate the likelihood of purchasing the product (e.g., prescribing the drug) upon seeing each profile. Obviously, there is quite a cognitive burden on consumers to rate each of 162 profiles. It has been well documented that a consumer should rate no more than 30 profiles at any given time. A product may have more than five attributes and in today’s competitive market, the number of attributes in a marketing research study could be well above 10. As a result, the total number of profiles based on a full factorial design is usually too large. As such, a fractional factorial design is usually used.
A fractional factorial design selects only a subset of the profiles based on a full factorial design so that the number of profiles can be handled relatively easily by respondents, while each attribute and the attribute level can also be assessed adequately. Thanks to the advance of computer technology, most statistical packages such as SAS, SPSS, and Sawtooth (CVA, 2000) can generate fairly quickly a fractional factorial design. Two criteria that are frequently mentioned in literature in evaluating a fractional factorial design are orthogonality and balance. The former refers to a design where the effect of each attribute can be evaluated independently. This is important because only by an orthogonal design will the effects will be uncorrelated to each other, thus avoiding possible confounding problems. The balanced design refers to the design in which levels of attributes are equally represented in the design, so that the effects are also uncorrelated with the intercept and the design becomes more efficient.
The number of profiles
How many profiles do we need to have from a fractional factorial design? There is no absolute number to follow; the answer depends on the number of attributes and attribute levels, as well as the level of efficiency for the design. It is generally perceived that if there are n attributes with an average of k levels, we need to have n (k - 1) + 1 parameters and the total number of profiles equals to about 1.5 times of the number of parameters. With five attributes having three levels of each, for instance, there would be 11 parameters (5 (3 - 1) + 1) and thus about 16 tasks to complete.
Here, we give a rough range of the number of profiles rather than a concrete number to follow. This is because when a fractional factorial design is implemented, the choice of the final number of profiles depends on other factors such as the efficiency of the design itself. Briefly, the efficiencies refer to the measure of design goodness. For those who are interested in knowing about the efficiencies, please see the paper by Kuhfeld et al (1994).
The number of profiles increases for a segmental experiment. For instance, in evaluating the effects of a headache treatment, the three types of patients (tension, migraine, and cluster) may be identified, and they differ in the types of treatments received. If we want to hold their treatment type constant across the attributes and attribute levels, we would need three times more of the number of profiles we have generated.
The numbers of levels of the attributes should be about equal. Consumers may place high value on the importance of an attribute with many levels. Therefore, an attribute with more levels may be weighted more important than an attribute with fewer levels. (Wittink, Krishnamurthi and Reibstein, 1989). The importance of an attribute with more levels will be inflated.
Rating and ranking methods
There are many different types of methods for assessing consumers’ preferences for a certain product. Among these, rating and ranking are frequently used with conjoint studies.
Rating methods, as noted by marketing researchers (Green, and Tull, 1978), are some of the most popular and easily applied data collection methods. In a conjoint analysis, for instance, a physician is asked to indicate the likelihood of prescribing that product upon seeing each profile. The rating scale ranges from 1 (definitely no) to 7 (definitely yes). Other rating scales, from 1 to 5 or from 1 to 9 are also used as well. The ranking method, on the other hand, requires physicians to order each of the profiles based on the likelihood of prescribing the product. If we have a total of nine profiles, all profiles will be ranked from 1 to 9, with a lower number usually indicating the product most likely to be prescribed by the physicians. Usually no ties are allowed.
3. Sample size
The sample size required for the conjoint analysis is debatable because there is no definite rule to follow.
Before we calculate the sample size for a conjoint analysis, we need to calculate the number of parameters. As mentioned earlier, usually the total number of parameters is equal to the total number of levels (all levels for all attributes combined) minus the total number of attributes plus one. For example, say we have four attributes with three levels for each and one attribute of two levels (see the example in Table 1). We would have a total of 14 (3 x 4 + 2) levels. We then have 10 parameters (14 – 5 + 1).
The rule of thumb for the ratio of the number of parameters to the number of respondents is between five and 10. In other words, if we have four attributes with three levels each and one attribute of two levels, we then need at least 50 physicians (10 parameters x 5) to complete the study. If we have 10 attributes with three levels each, we then have 21 parameters (30 – 10 + 1) and need at least a sample size of 105. Most researchers in conjoint analysis agree that we need probably at least 70 to 100 respondents to make the results stable.
Data analysis
Utilities
In a conjoint analysis, a consumer’s preference (rating or ranking) is the dependent variable and product attribute levels are the independent variables. Note here that the dependent variable can also be a binary preference intention (e.g., yes versus no) or constant sum (e.g., For the next 10 patients you are going to treat, how many patients you are to prescribe this drug?). The coefficients in the regression model are the estimated part-worth utilities. As in a regression analysis, the R-square gives an indication on how the data fit the model. The R-square tells the proportion of the variance of the consumer’s preference that is explained by the combination of the independent variables (attributes and attribute levels). While its values range between 0 to 1, a high value of R-square would indicate the data fit the model well. On the other hand, if the R-square is low, there is an indication that data may not fit the model well, either because there are some errors in the data collection or some inconsistency while consumers perform their rating or ranking tasks.
Relative importance of an attribute
The relative importance value shows how important an attribute is in affecting consumers’ preference for a product. It is derived from the part-worth utilities for each attribute. First, the range of the attribute is computed for each attribute by subtracting the smallest part-worth utility from the largest one; second, the total range is computed by adding the ranges for all attributes together; third, the relative importance value is computed by dividing the range of the attribute by the total range.
Two methods that are frequently mentioned in literature are metric and non-metric. The key difference between metric and non-metric conjoint analysis lies in how the dependent variable (rating or ranking) is transformed. For metric conjoint analysis, a linear transformation is performed and the original rating or ranking data is unchanged. For non-metric analysis, a monotone transformation is conducted. In this monotone transformation, the order of the rating/ranking is preserved but the data have been transformed to make the model fit better. For these reasons, the R2 in non-metric conjoint analysis is always higher than that of metric analysis; however the former is also less stable than the latter. In general, metric conjoint analysis is used more often than non-metric conjoint analysis.
Validation
In quantitative marketing research, we often need to validate the model. In a common regression model, for instance, we may develop a model based on the first group of 100 consumers. We then apply the regression coefficients derived from the model to the second group of consumers. The high correlation between predicted value and actual values for the second group will indicate that the model has good predictive power. Similarly, we can also do it in conjoint analysis by using “holdout observations.”
In conjoint analysis, the observations used for developing a model are commonly referred as “actual observations,” which is different from “holdouts.”
Holdout observations are used to validate the model and to calibrate the simulator. The profile for validation is a hypothetical product that is rated or ranked by consumers but is not used in the estimation of utility values in the model. The purpose of having holdout observations is to determine internal validity of the model by examining the associations between the actual and predicted ratings for these observations. Usually, the number of holdouts is small because these profiles, though not used in estimating the model, add to the burden placed on respondents. We should not increase unnecessarily the burden on consumers when they are performing tasks. These holdout observations are normally derived from those that are included in a full-factorial design but not in fractional factorial design. In the example we referred to earlier, there are 81 profiles for a full-factorial design with four attributes with three levels each. If the fractional factorial design only has the 24 profiles selected from the 81, the holdout observations will be derived from the 57 remaining profiles that are left out.
The validations assessed through the holdout observations are calculated based on the magnitudes of correlation coefficients between the predicted values of these holdout observations and their actual values. The ranges of correlation coefficients are between –1 to +1. In the evaluation of the validity of model, a positive moderate magnitude of correlation coefficient is usually needed. Note that the magnitude of the correlation coefficient depends on many other factors such as sample size (in this case the number of holdout observations and the number of profiles) and variation of the predicted and actual values. Another indicator for the assessment of the model would be the p-value associated with the level of the significance (e.g., .05 or .01).
Simulating market share
As we have indicated earlier, one of the objectives in using conjoint analysis is to simulate market share. In other words, after the model is developed, we want to know how many times a consumer will purchase the new product, or in the example cited earlier, how many times a physician will prescribe the drug. Note that a simulation of market share can be performed both for a new product and for an existing product.
In a conjoint study, the overall utility score associated with each drug is calculated based on the utility values of each attribute level for that drug. One way to simulate the market share is to assume that physicians will prescribe the drug with the highest utility value. It is particularly useful for a hypothetical product because the simulator predicts how physicians will react to changes in certain attribute levels based on the utility values estimated from the model.
Limitations
1. Conjoint analysis applies a regression model which uses attributes and attribute levels to predict the likelihood of purchasing a product. In the model, we have to decide the attributes and attribute levels that are identifiable and important to the consumers. In a research project for a pharmaceutical manufacturer, for instance, we identify those attributes such as price, efficacy, side effects, etc., that are important in physicians’ decisions to prescribing drugs. However, in defining the attributes and levels, we may not be as inclusive as we should.
2. Conjoint analysis is mainly concerned with main effects. It ignores the possible interaction effects among the attributes and levels. For instance, price and brand interaction (i.e., different brands may have different price sensitivities) is difficult to estimate in a traditional conjoint study.
3. When the number of attributes and attribute levels gets very large, it is difficult to justify the use of traditional conjoint analysis. In such cases, we either have to use a special type of conjoint analysis such as adaptive conjoint (Sawtooth, 2000) or we have to increase the sample size so that the rating or ranking tasks can be divided among the respondents. See Johnson (1991) for more on adaptive conjoint analysis.
4. Conjoint analysis usually requires that the number of levels for each attribute is about equal. For instance, if one attribute has two levels and the other six levels, the range of utility values for the six-level one will likely be higher than the two-level one simply because one attribute has more levels than another.
5. Conjoint analysis usually dictates that the values of levels are the same across the attributes. For instance, one of the requirements in using conjoint analysis is that the levels of price are the same across the drugs, which is sometimes not the case. For this reason, a discrete choice modeling is suggested, which we will discuss in another article.
References
Acito, F. and Jain, A.K. “Evaluation of conjoint measurement results: a comparison of methods.” Journal of Marketing Research. 1980,17:106-112.
Currim, I.S., Weinberg, C.B. and Wittink, D.R. “The design of subscription programs for a performing arts series: Issues in applying conjoint analysis.” Journal of Consumer Research. 1981;8: 67-75.
CVA System. Version 2.0. Sawtooth Software, Sequim, WA. 2000.
Graf, M.A., Tanner, D.D. and Swinyard, W.R. “Optimizing the delivery of patient and physician satisfaction: A conjoint analysis approach.” Health Care Management Review; 1993;18:34-43.
Green, P.E. and Rao, V.R. “Conjoint measurement for quantifying judgmental data.” Journal of Marketing Research. 1971, 8:355-363.
Green, P.E., Tull, D.S. Research for Marketing Decisions. (4th Edition). Prentice-Hall, Inc, Englewood Cliffs, New Jersey, 1978).
Green, P.E. and Wind, Y. “New way to measure consumers’ judgments.” Harvard Business Review, 1975. July-August, 107-117.
Johnson, R.M. “Trade-off analysis of consumer values.” Journal of Marketing Research. 1974, 11:121-127.
Johnson, R.M. “Comments on studies dealing with ACA validity and accuracy, with suggestions for future research.” Sawtooth Software Working Paper, May 1991.
Kuhfeld, Tobias and Garratt. “Efficient experimental design with marketing research application.” Journal of Marketing Research. 1994;31 (November):545-557.
Louviere, J.J. Analyzing Decision Making, Metric Conjoint Analysis. Sage University Papers, Beverly Hills: Sage 1988.
Norman, K.L. A case for the generalizability of attribute importance: the constant ratio rule of effects. Organizational Behavior and Human Performance. 1980;25:289-310.
Sawtooth Software Inc., ACA system adaptive conjoint analysis, Version 4.0 Sawtooth Software Inc., 2000. www.sawtoothsoftware.inc.
Wittink, D.R., Krishnamurthi, L., and Reibstein, D.J. “The effect of differences in the number of attribute levels in conjoint results.” Marketing Letters, 1989;1L2): 113-123.