Editor's note: Steven Struhl is director of the Marketing Sciences Group of SDR Chicago.
Classification tree methods greatly expand the ways in which you can analyze, view, and consider survey data and other information. They provide some highly valuable new tools for data analysis. With these methods, you can:
- cluster with a dependent variable, allowing you to develop segments in one step;
- assign "don't know" and "refused" respondents into groups, along with those who answered;
- generate simple rescoring models you can use with a pencil and paper, in later studies or for screening purposes;
- analyze continuous, ordinal, and categorical data (including yes/no variables) in one analysis;
- investigate conditional probabilities, allowing you to find low-incidence groups easily.
These procedures produce a classification tree by splitting a sample into sub-groups, then repeating this splitting within the sub-groups formed again and again until you reach some pre-set limit (see figure 1 for a section of a classification tree). The sample gets split to maximize differences (variance) between these sub-groups on some dependent variable. Such a variable could be, for instance, buying intentions, overall ratings, cluster group membership, or product use level.
Several related procedures with different capabilities produce classification trees. CHAID (or chi-squared automatic interaction detection) probably remains the most popular of these. It has salient advantages over traditional AID, which fell into disuse because of its relative inflexibility and analytical shortcomings. (Later sections will discuss these differences more fully.) CHAID/CART (CHAID and Classification and Regression Tree) analysis provides an even more flexible approach than CHAID, but is relatively new and unknown. The first few sections of this article refer mostly to CHAID; later sections discuss both CART and CHAID.
Forming segments in one step
Because you divide the sample to maximize differences between sub-groups (on some criterion you choose), you automatically get segments, rather than groups or clusters. True segments vary in response to some marketing-related variable; without such variation, you may have split the sample, but only into groups. So, if you divide your sample into sub-groups that differ in purchase intent (for instance), then you know these sub-groups are in fact segments.
Clustering by more traditional methods provides no such guarantee. You may have to cluster respondents several different ways to find a scheme that produces between-group differences on any marketing-related variable. Even then, you do not know if your clustering procedure has maximized these differences or if it even has come close to doing so.
A typical classification tree analysis (either CHAID or CHAID/CART) will split the sample into 8 to 30 (or so) groups. You can then combine these into as many segments as you wish, grouping together sub-groups in ways that make the most sense.
Revealing conditional probabilities
By splitting the sample again and again, CHAID and CHAID/CART can show you conditional probabilities, as follows. Suppose you have done a survey and now want to differentiate "Brand Z" purchasers from non- purchasers. The procedure might find that Brand Z buyers, 20% of the overall sample, make up 60% of those with incomes of $35,000 to $50,000. This income group would get split off from all others, who have only a 12% incidence of Brand Z purchasers.
The "purchaser-rich" sub-group would again get split, resulting in another, smaller sub-group with a particularly high incidence of purchasers. (Of course, another sub-group having a lower incidence of purchasers also would be produced in this process.) This could then continue, with further splits identifying groups with still higher incidences of buyers. The second split, and all later splits, here would be conditional upon the first. Eventually, you would find "pockets" where Brand Z buyers you seek are highly prevalent.
An example
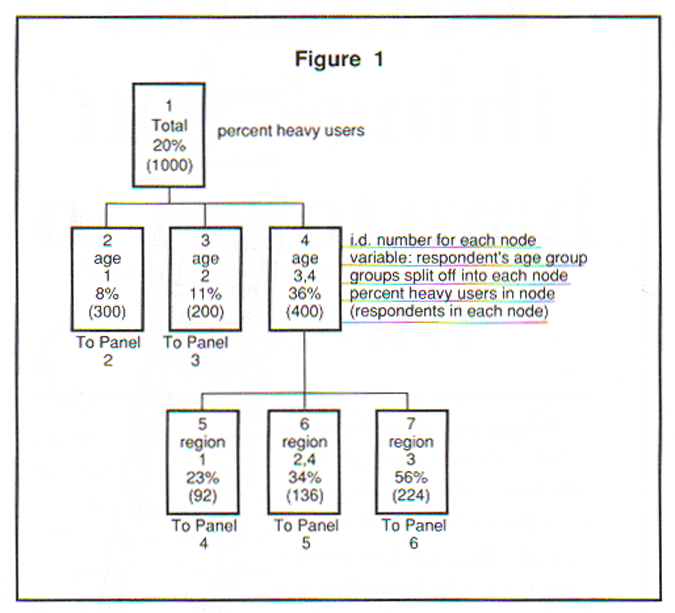
Let's look at a slightly more complicated example. Suppose you want to find what most distinguishes light from medium from heavy users of Product Y, based on responses to 80 question items, including demographics. (This fictional example appears on the sample tree diagram on the next page. You may wish to refer to this diagram along with the description below.)
Using CHAID or CHAID/CART, you would first split the sample on one of the variables producing the greatest between-group differences in purchase. Suppose this variable is the respondent's age group. Looking just at the heavy users, you would then see that they make up:
- 20% of the sample overall;
- 11% of the 25-34, and
- 8% of the 18-24 age group;
- 36% of the 35-54 group.
In addition, the procedure created this last group by combining two groups defined in the questionnaire, those age 35-44 and those age 45-54. These groups got combined because incidence of light, medium and heavy purchasers did not vary significantly between them.
The procedure would then continue within each group devised in the last step. Looking just at the 35-54 age group, suppose you then find that region of the country best differentiates between light, medium, and heavy users. Region 3 (Midwest) has the highest incidence of heavy users within the 35-54 year age group (56%), while region 4 (South) has the lowest incidence (23%). The procedure here combined regions 2 and 4 (East and West) into one group. The level of incidence of heavy users in this last group was 34%.
Note that the very high incidence group just uncovered must first be age 35-54 and next live in the Midwest. One condition must precede the other in this analysis. We would not have found this fact simply by looking at the total sample. This is where the conditional probability comes in.
As the example showed, CHAID and CHAID/CART can perform "optimal recoding" of independent variables, rearranging codes to maximize separation of the groups specified by the dependent variable. You can specify whether the codes can combine freely (in any order), or whether they must get grouped in sequence.
Assigning "don't know" and "refused" responses
CHAID and CHAID/CART also can assign "don't know" responses to the group (or groups) that will maximize differences on the dependent variable. This can come in handy on questions where some percentage of respondents are unwilling or unable to answer, such as household income questions. Of course, assigning the "don't know" group along with others makes most sense when the majority of respondents answer. If you have much over 15% "no answer" (for whatever reason), you may want to think about either keeping the question out of the analysis, or treating those who "refused" as a separate group that cannot combine freely with any others.
Classification tree output: sections of a tree diagram
Crucial to the output is a tree structure that shows, at each stage:
- The independent variable you selected from those best dividing the sample, and how the sample splits on that variable,
- The number of individuals "split off" into each of the groups,
- Key dependent-variable values among each of the groups split off (for example, the percentage of heavy users in each sub-group),

CHAID produced the tree diagram from which we took section shown above. Trees displays produced by CHAID can show other information as well, or suppress some of the detail shown. A table giving a complete breakdown of each split, showing the incidence of all groups at each point in this diagram, usually follows CHAID also can produce highly detailed summaries of every step in its analysis. These show how the sample split, best and other significant predictors at each point, and so on. A complete CHAID history can use 2 megabytes to 5 megabytes of disk space, and cover hundreds of pages.
CHAID versus traditional AID
CHAID represents a significant advance over traditional AID Although once in widespread use, traditional AID is rarely seen today because of its relative shortcomings.
Traditional AID was limited to bifurcating the sample (splitting it in two). This had the effect of allowing variables with several codes to "explain" more variance than dichotomous ("yes/no") questions. This happened because there are many ways to combine a large number of codes into two groups - and the more codes, the more possible combinations. Odds of finding some "highly-predictive" split therefore would rise as the number of codes increases. Variables with several codes would have the best chance to "float to the top," appearing as the best explanatory variables.
However, CHAID (and CHAID/CART) allow the sample to be split into as many as 15 groups (depending on how many codes the best predictor has) at any point in the tree. They also have procedures for adjusting the observed significance of a variable for the number of codes a variable has. This gives all variables a more even chance to appear in the analysis, regardless of their type (long scale, short scale, or yes/no).
Limitations of CHAID
While CHAID was designed to process non-metric and non-ordinal data that normal multivariate analyses cannot handle, it has certain limitations:
- Data must be ordinal, nominal or interval, and not metric. No variable can have more than 15 levels. Any variable having more than 15 levels, and all metric variables, must get recoded to no more than 15 categories.
- You must specify a "response" or dependent variable. This is similar to the grouping variable in discriminant analysis. CHAID will partition the sample to maximize between-group differences (variance) on this variable. If you have no such dependent variable, CHAID will not run. You can, though, run CHAID using such dependent variables as segments generated by a clustering procedure, to look at the data in a different way.
Note that CHAID cannot perform analyses with continuous dependent variables, such as number of packages of the product bought. You must either recode such variables, or use CHAID/CART, which the next section discusses.
- CHAID cannot process zero values or codes that are not in sequence (for instance, you cannot skip from a code "3" to a code "6"). This may add to the time you must spend recoding data.
CHAID/CART versus CHAID
The CHAID/CART algorithm provides even more flexibility in handling data than CHAID. CHAID/CART allows for both continuous and categorical variables, both as dependent and independent variables. Using continuous dependent variables, CART procedures search for ranges in which the dependent variable does not vary significantly on the predictor variable. With continuous variables on both sides of the equation, these calculations can become highly complex.
Available CHAID/CART algorithms also can handle missing values and non-continuous codes more intelligently than current versions of CHAID. With CHAID/CART procedures, missing values can be left blank, and codes do not need to follow in strict sequence. (If you, for instance, have families with I, 2, 3, 4, and 8 children in your sample, you do not have to recode the "8" to a "5.")
The greater complexity of CHAID/CART leads to its one relative disadvantage versus CHAID: it takes more time to analyze data. With samples of the size usually used in market research, this speed difference will be small. With databases having many thousand respondents, CHAID will have a definite speed advantage.
Decision models based on classification tree analyses
Any classification tree procedure can lead to a set of decision rules simple enough to be used with a pencil and paper. After determining how a given respondent fits the conditions from each rule, you will get a predicted value on your dependent variable for that respondent. You typically can use these rules much more easily than the predictive models generated by such procedures as regression, discriminant or logit/probit analysis. 
The rules below match the tree on the preceding page. You could even use such rules in quick screening of respondents, for example, in mall interviews. Referring to these and the tree diagram, you could generate a set of questions with skip patterns that would quickly give you a predicted consumption level for new respondents not in your original survey. 
CHAID and CART vs. traditional multivariate procedures
You can use CHAID and CHAID/CART interactively, choosing from among variables that will lead to significant differences between groups formed on your dependent variable. You typically will have many possible variables on which you could split the sample, at least in early stages of the analysis. You can usually find one or more ways to split the sample that makes sense in terms of your organizational goals and abilities.
You can also use these procedures to examine alternative splits in "what-if' type analyses. These procedures' interactive capabilities make them ideal for investigating patterns in your data. Of course, if your only interest is the model that maximizes variance, you can run these procedures in automatic mode.
Because CHAID and CART work by sequential procedures, you do not need to specify an explicit "effects" model as you might with, for instance, analysis of variance. Unlike standard multivariate procedures, CHAID and CART analyze groups based on conditional probabilities, which can provide valuable insights that other procedures will not. Both CHAID and CHAID/CART procedures require highly flexible and "smart" algorithms to compare all the types of variables that they handle. CHAID/CART in particular applies rules in ways that approach artificial intelligence.
These procedures therefore constitute one "cutting edge" of data analysis. They provide a new and efficient way to develop segments, that is, groups that definitely will vary in terms of some key variable. The procedures' newness and sophistication, though, have a price. Both require some explanation and "training" of clients. Perhaps as a result, both still receive less use than they merit.