Editor’s note: Stephen J. Hellebusch is president of Hellebusch Research & Consulting, Inc., Cincinnati.
The logic of statistical (stat) testing is not complex, but it can be difficult to understand, because it is the reverse of everyday logic and what normal people expect. Basically, to determine if two numbers differ significantly, it is assumed that they are the same. The test then determines whether this notion can be rejected, and we can say that the numbers are “statistically significantly different at the (some predetermined) confidence level.”
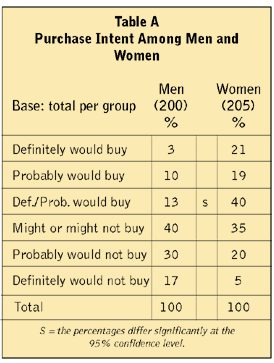
 While it is not complex, the logic can be subtle. One subtlety leads to a common error, aided and abetted by automatic computer stat testing - overtesting. Suppose there is a group of 200 men and one of 205 women, and they respond to a new product concept on a purchase intent scale. The data might look like that shown in Table A.
While it is not complex, the logic can be subtle. One subtlety leads to a common error, aided and abetted by automatic computer stat testing - overtesting. Suppose there is a group of 200 men and one of 205 women, and they respond to a new product concept on a purchase intent scale. The data might look like that shown in Table A.
Statistical logic assumes that the two percentages to be tested are from the same population - they do not differ. Therefore, it is assumed that men have the same purchase interest as women. The rules also assume that the numbers are unrelated, in the sense that the percentages being tested are free to be whatever they might be, from 0 percent to 100 percent. Restricting them in any way changes the probabilities, and the dynamics of the statistical test.
The right way to test for a difference in purchase intent is to pick a key measure to summarize the responses, and test that measure. In Table A, the Top Two Box score was tested - the combined percentages from the top two points on the scale (“definitely would buy” plus “probably would buy”). Within the group of men, this number could have turned out to be anything. It just happened to be 13 percent. Within the group of women, it could have been anything, and, as it turns out, was 40 percent. Within each group, the number was free to be anything from 0 percent to 100 percent, so picking this percentage to test follows the statistical rule. The stat test indicates that the idea that these percentages are from the same place (or are the same) can be rejected, so we can say they are “statistically significantly different at the 95 percent confidence level.”
 Something different often happens in practice, though. Since the computer programs that generate survey data do not “know” what summary measure will be important, these programs test everything. When looking at computer-generated data tables, the statistical results will look something like those shown in Table B.
Something different often happens in practice, though. Since the computer programs that generate survey data do not “know” what summary measure will be important, these programs test everything. When looking at computer-generated data tables, the statistical results will look something like those shown in Table B.
If the Top Two Box score is selected ahead of time, and that is all that is examined (as in Table A), then this automatic testing is very helpful. It does the work, and shows that 13 percent differs from 40 percent. The other stat test results are ignored. However, if the data are reported as shown in Table B, there is a problem.
The percentages for the men add to 100 percent. If one percentage is picked for testing, it is “taken out” of the scale, in a sense. The other percentages are no longer free to be whatever they might be. They must add to 100 percent minus the set, fixed percent that was selected for testing. Percentages for the men can vary from 0 percent to 87 percent, but they can’t be higher, because 13 percent is “used up.” Similarly, percentages for the women can vary from 0 percent to 60 percent, but 40 percent is used already. When you look at testing in the other rows, or row by row, you are no longer using the confidence level you think you are using - it becomes something else.
Statistically, if one said of Table B that the percentages that “definitely would buy” and the percentages that “definitely/probably would buy” both differ at the 95 percent confidence level, it would be wrong. One of them does, but the other difference is at some unknown level of significance, probably much less than 95 percent, given one related significant difference.
Stat tests are very useful. Each one answers a specific question about a numerical relationship. The one most commonly asked about scale responses is whether two numbers differ significantly. If they are the right two numbers, and the proper test is used, the question is easily answered. If they are the wrong two numbers, or the wrong test has been used, the decision maker can be misled.