Editor's Note: Betsy Goodnow is marketing research manager of the Fact Flow Research Division of Donahoe and Purohit Inc., Rosemont, IL. She is also president of Market Action Research Software, Inc., Clarendon Hills, IL.
The debate between spokesmen for multiple correspondence analysis (MCA) and correspondence analysis (CA) has a long history. Karl Pearson (1913) developed the antecedent of CA used by Procter & Gamble (Horst 1935). R.A. Fisher (1940) named the approach "reciprocal averaging" because is reciprocally averages row and column percents in table data until they are reconciled.
The qualitative approach
Prior to U.S. entry into World War II, Louis Guttman (1941) developed a "qualitative" approach to CA named optimal (or dual) scaling. This "ANOVA-like" approach optimizes the correlation among row and column categories in tables. With optimal scaling Guttman proved that the Simon-Binet intelligence test is a "perfect" scale for classifying draftees. The scale is ordinal because a perceptual map of test results approximates a horseshoe-shaped parabola.
The quantitative approach
Since reciprocal averaging was inefficient, Europeans such as Mosaier (1946) and Benzecri (1969) related table data with computer programs for principal component (factor) analysis. Burt (1953) criticized their quantitative analysis of "qualitative" table data in a journal article. To circumvent this problem, Burt developed MCA (homogeneity analysis) of a binary indicator (or Burt) matrix.
The winner
In response to Burt's article (1953), Guttman reports that optimal scaling is mathematically equivalent to factor analysis. "The two systems are identical..." According to Guttman,
the two approaches developed independently because the war broke down communication between the Americans and the Europeans. Guttman notes, "The British use factorial procedures for both quantitative and qualitative data, but Americans...fail to discuss material of this kind of all." Evidently, Burt won the debate by convincing the statistical community that quantitative analysis of tables with CA is inappropriate.
Did the best approach win?
The purpose of this article is to shed new light on the debate and to prove beyond a doubt that Burt was wrong. The objectives of this study are to demonstrate the following:
1. Table data is appropriate for quantitative analysis
2. Burt matrix data is not appropriate for quantitative analysis
The first section presents an example of MCA and demonstrates why the Burt matrix does not fulfill requirements for quantitative analysis. The second section presents an example of CA and proves why CA does fulfill these requirements.
Example of MCA
The Burt Matrix
The purpose of this simple hypothetical example is to describe perceptions of a product on three traits. These traits are TOP (most popular), BIG (biggest size), and LOW (lowest price). The 18 respondents check all traits that describe the product. The raw data of their responses and their gender are reported in the following binary indicator (Burt) matrix.
Burt Matrix
|
Top |
Big |
Low |
Male | ||||||
|
Joe |
1 |
0 |
1 |
1 | |||||
|
Ann |
0 |
1 |
1 |
0 | |||||
|
Roy |
1 |
1 |
1 |
1 | |||||
|
Nan |
0 |
1 |
1 |
0 | |||||
|
Sam |
1 |
1 |
0 |
1 | |||||
|
Liz |
0 |
1 |
0 |
0 | |||||
|
Bob |
0 |
0 |
1 |
1 | |||||
|
Peg |
0 |
0 |
1 |
0 | |||||
|
Dan |
1 |
1 |
1 |
1 | |||||
|
Meg |
1 |
1 |
1 |
0 | |||||
|
Art |
1 |
0 |
1 |
1 | |||||
|
Kay |
1 |
0 |
1 |
0 | |||||
|
Ray |
1 |
1 |
1 |
1 | |||||
|
Joy |
1 |
0 |
1 |
0 | |||||
|
Ned |
1 |
1 |
0 |
1 | |||||
|
Gay |
1 |
0 |
0 |
0 | |||||
|
Nat |
0 |
1 |
0 |
1 | |||||
|
Jan |
1 |
0 |
0 |
0 |
Interpretation
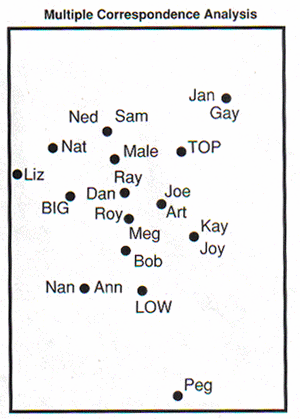
MCA of the responses is presented by the following perceptual map.

The positions of the points on the map show that the responses of the following people are identical: Jan and Gay, Ned and Sam, Art and Joe, Nan and Ann, Joy and Kay, as well as Roy, Ray and Dan. Since Roy, Ray, and Dan perceive that the product has all traits, MCA positions them at the origin of the map. (Meg also checked three traits so MCA should position Meg at origin. However, Meg's gender affected her position relative to the traits.) Since Peg, Liz, Jan, and Gay perceive the product as having only one trait, MCA positions them far from the center and near that trait. (Bob and Nat also checked only one trait so MCA should position Bob and Nat the same way. However, gender affected their position relative to the traits.) Since Joe and Art perceive the product as having two traits, MCA positions them between those traits. (Gender also affected the position of others who checked two traits. When MCA mixes variables, the solution is not interpretable.)
Broken assumptions
The reason the solution lacks face validity is that the data is not appropriate for such quantitative analyses as MCA. Data in a binary indicator (Burt) matrix does not fulfill requirements for MCA.
1. The data are binary, not truly metric.
2. The data has a poisson (highly skewed) distribution, not a bivariate normal distribution.
3. The data's unit of measurement for traits and gender male are not consistent. MCA weighs gender three times more important than traits.
4. The data lacks enough degrees of freedom for a stable solution.
Evaluation of MCA
According to Kent (1986), MCA is a "misspecified model where we 'pretend' the discrete data follows a multivariate normal distribution." Van Rijckevorsel and Worsley (1988) warn, "It is absolutely necessary to investigate the stability of the results." Kaciak and Louviere ( 1990) conclude that MCA may yield uninterpretable maps.
Example of CA
The Table
The first six respondents in the previous Burt matrix are assigned to Subgroup A, the next six to Subgroup B, and last six to Subgroup C. The responses of each subgroup are aggregated and reported in the following table.
Table
|
Top |
Big |
Low |
Male | ||||||
|
A |
3 |
5 |
4 |
3 | |||||
|
B |
4 |
2 |
6 |
3 | |||||
|
C |
5 |
3 |
2 |
3 |
Correspondence analysis
CA of the responses is shown in the following perceptual map.

The position of the points on the map indicates that Subgroup A perceives the product is big in size, Subgroup B perceives the product is low in cost, and Subgroup C perceives the product is top in popularity. In contrast to the solution of MCA, the solution to CA has face validity.
Fulfilled assumptions
Table data is appropriate for quantitative analysis since it fulfills all assumptions for quantitative approaches to CA.
1. The data are truly metric because cell values (frequency counts) are the input data (Goodnow 1991).
2. A table with nine cells approximates a bivariate normal distribution (Pearson 1913).
3. The data's unit of measurement for male need not be consistent with traits because male is a passive category. Each passive category is individually superimposed on the solution (Lebart, Morineau and Warwick 1984). In contrast to MCA, gender does not affect the solution.
4. All solutions to CA best summarize relationships among categories (Nishisato 1984) and this solution is significant.
Summary
Over 50 years ago famous statisticians such as Pearson, Fisher, and Guttman developed qualitative approaches to CA. Burt considered quantitative approaches inappropriate since tables crosstabulate qualitative data. To circumvent this problem, Burt proposed MCA of a Burt matrix. Much to his chagrin, this article demonstrates that data in a Burt matrix is inappropriate for such quantitative analysis as MCA. However, the frequency counts of cell values in table data is metric, has a bivariate normal distribution, allows for different units of measurement, and has ample degrees of freedom. Thus the author recommends quantitative approaches to CA and agrees with Van Rijckevorsel and Worsley (1988), "Homogeneity analysis is a dangerous technique."
References
Benzecri, Jean Paul (1969), "Statistical Analysis as a Tool to Make Patterns Emerge from Data," in Methodologies of Pattenn Recognition, S. Watanabe, ed. New York: Academic Press: 35-74.
Burt, C. (1953), "Scale Analysis and Factor Analysis," The British Journal of Statistical Psychology, 6:1 (May) 5-23.
Fisher, Ronald A. ( I 940), "The Precision of Discriminant Functions," Annuals of Eugenics 10 (December), 422-9, cited in Michael J. Greenacre, Theory and Applications of Correspondence Analysis, London: Academic Press.
Gittins, Robert (1990), Review of Abby Israels, "Eigenvalue Techniques for Qualitative Data," Psychometrika, 55:1 (March 1990) 177-181.
Goodnow, Wilma Elizabeth (1991), "Correspondence Analysis," speech presented to Paul Green and his graduate class in marketing research, Wharton College of Business, University of Pennsylvania, October 23.
Gutunan, L. ( 1941), "The Quantification of a Class of Attributes: A Theory and Method of Scale Construction," in The Prediction of Personal Adjustment, P. Horst et al, ea., New York: Social Science Research Council, 31948.
Horst, P. (1935), "Measuring Complex Attitudes," Journal of Social Psychology, 6, 369-74.
Kaciak, Eugene and Jordan Louviere (1990), "Multiple Correspondence Analysis of Multiple Choice Experiment Data," Journal of Marketing Research 27 (November) 455-65.
Kent, J.T., Discussion of Goodman, Leo A. (1986). "Some Useful Extensions of the Usual Correspondence Analysis Approach and the Usual Log-Linear Models Approach in the Analysis of Contingency Tables," International Statistical Review 54:3, 243-309.
Lebart, Ludovic; Morineau, Alain, and Kenneth M. Warwick (1984), Multivariate Descriptive Statistical Analysis: Correspondence Analysis and Related Techniques for Large Matrices, New York: John Wiley and Sons.
Mosaier, C.1. (1946), "Machine Methods in Scaling by Reciprocal Averages," Endicon, NY: IBC Proceedings Research Forum, 35-9.
Nishisato, Shizuhigo (1 984j, Analysis of Categorical Data: Dual Scaling and Its Applications, Toronto: University of Toronto Press.
Pearson, K. (1913), "0n the Measurement of the Influence of 'Broad Categories' on Correlation," Biometrika 9, 116-39.
van Rijekevorsel, J. and Keith J. Worsley (1988), "Comment on Correspondence Analysis Used Complementary to Loglinear Analysis," Psychometrika (May) 53:2, 287-91.