Editor's note: Stephen Hellebusch is president of Hellebusch Research and Consulting.
Some readers may already be familiar with the Monty Hall problem but a brief description can’t hurt. On the venerable TV game show Let’s Make A Deal, the host, Monty Hall, would have three doors. Behind one was a valuable prize like a new car or a dream vacation. Behind each of the other two was a booby prize of some kind like a goat or an old junker. The contestant (you) was asked to pick a door. With no knowledge, it is a one-in-three chance you will pick the car. So, you pick Door 1 at random.
Then, Monty shows you that there is a goat behind Door 3 and asks if you want to switch from Door 1 to Door 2. Logically, it seems it shouldn’t matter. Your odds are now 50/50, so why not just stay with Door 1? Makes no difference.
Statistically that is wrong. Monty has just given you new information and it changes the odds. Given that there is a goat behind Door 3, your odds increase significantly if you switch to Door 2. Honestly, I have never understood completely why this is so. So, I decided to conduct a thought experiment and see for myself.
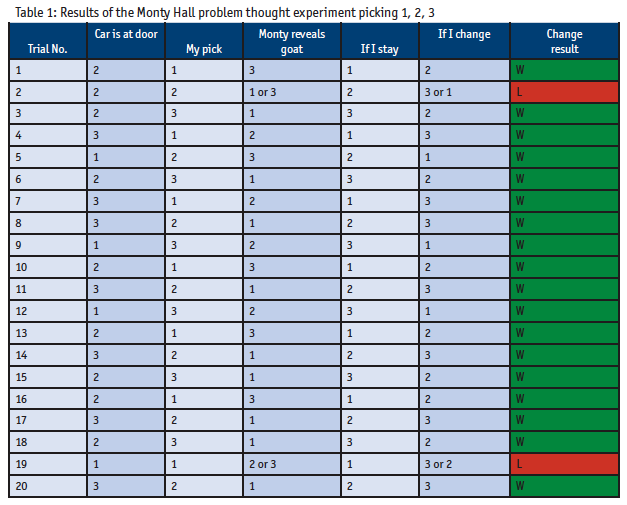
I took a die and rolled it 20 times. I thought I would start with 20 and see if any pattern emerged. If the die came up 1 or 4, the car was behind Door 1. If it came up 2 or 5, it was behind Door 2, and 3 or 6 was Door 3. Then, I did choices. For the first three trials I picked Door 1, 2, 3. Then, I just repeated that 1-2-3 pattern. It turned out to be amazingly unlucky in picking the right door on my first pick.

After that, I noted the door I would have if I stayed or if I switched and whether switching resulted in a win or a loss (Table 1).
Obviously, I won a lot more when I switched. I found this hard to believe (and still did not understand), so I did a variation. I kept the door the car was behind the same as in the set above, but I always picked Door 1. Staying with my pick, I won two more times (Table 2) than I did in my first thought experiment!

If my first guess is wrong, the door Monty opens is severely restricted, which is why changing your pick works better. For example, if the car is behind Door 2 and I pick Door 3, Monty must open Door 1. He can’t open Door 2 and show where the car is and he can’t open my pick, Door 3, show a goat and then ask me if I want to change. If I stay with Door 3, I lose, but if I switch, I win.
If I happen to guess right the first time, I lose by switching. If the car is behind Door 2 and I pick Door 2, Monty can open either other door and if I switch, I lose. Since I will only be right a third of the time, my best bet is to switch. You win a third of the time if you stick with your first choice and two-thirds of the time if you change.
I understand why a little better now but it still defies common sense (in my opinion)!