A look at the power of the design, the formula and the brand in taste testing

Abstract

Using cola taste tests as a framework, the author explores the role and power of brand names and the design of the research process on consumer reactions and perceptions.

The power of three

Editor’s note: Neil Kalt is director, new methodologies, at Beta Research Corporation, Syosset, N.Y.

The overriding objective of most taste tests is to determine the comparative appeal of each product. Toward this end, the standard taste test presents two products with all signs of brand identity removed and controls for order effects by rotating the order of presentation. If assessing the impact of the brands is also an objective, respondents are asked to compare the two products a second time, only this time with the products branded.

While this design is unquestionably serviceable, there are things we can do to make it better:

1. We can increase the power of the design, which is the ability to detect a statistically significant difference when one exists. When we increase the power of the design, we’re also able to determine with considerable precision how noticeable the difference between the two products being tested is. The less noticeable it is, the more likely the brands are to drive product preferences. The more noticeable it is, the more likely the unbranded products are to determine product preferences.

2. We can use an explanatory framework that’s defined by the power of the brand - which is the extent to which the brands determine product preferences - and by the power of the formula - which is the extent to which product preferences are driven by the unbranded products.

Because power is a zero-sum proposition for any one product, the power of a product’s brand and the power of its formula are inextricably linked, the two interlocking parts of a whole. That is, within the context of a head-to-head comparison of two products, the greater the power of a product’s brand, the less the power of its formula. Conversely, the greater the power of a product’s formula, the less power its brand has.

An explanatory framework that’s defined by the power of the brand and the power of the formula provides perspectives - or ways of looking at and thinking about the issues - that yield valuable insights. For example, this framework led to an unusual test of the power of each brand in which the formula is held constant (see below).

When two products are compared, the power of each product’s brand and each product’s formula are the result of this particular comparison, and may be substantially different when either of these products is compared to another product. Still, getting a sense of the power of a product’s brand and the power of its formula when it’s compared to a key competitor can provide fresh insights into the reasons for its performance, insights that can make a difference in how effectively the product is marketed.

Three trials

Let’s look at a hypothetical example. Say that we want to find out how Pepsi stacks up against Coke. We begin by taking respondents through three trials in which the samples they’re given are not brand-identified. They are simply told that they’ll be sampling two colas in each trial.

In the first trial, respondents either sample Pepsi, then Coke, or Coke, then Pepsi. In the second trial, the order in which the two products were presented in the first trial is reversed. In the third trial, half sample Pepsi twice and half sample Coke twice. In a fourth trial, respondents compare Pepsi and Coke with the brands identified. Each respondent either drinks Pepsi first and Coke second, or Coke first and Pepsi second.

At the end of each trial, respondents indicate whether they prefer the first sample or the second, or whether they have no preference. Their choices, based on some combination of brand and formula, provide the baseline for the power of the formula and, to an extent, the power of the brand.

Order of presentation

The preceding design enables us to identify respondents whose preferences are governed by the order of presentation and/or who express a preference when the correct answer is “no preference.” As a result, we’re able to exclude these respondents from the analysis, which can increase the power of the design by increasing the ability of the statistical test we use to detect a difference when one exists. Let me explain.

The shortcomings of the standard design can result in a considerable amount of “noise.” Noise is data that make it more difficult to detect a significant difference when one exists. In the standard design, there are two sources of noise:

1. Respondents who make choices based on the order of presentation rather than on the differences between the products - that is, respondents who prefer different products on the first two trials.

2. Respondents who express a preference when they’re given two samples of the same product on the third trial.

The standard design, which is unable to distinguish between preferences based on the products and preferences based on the order in which they’re presented, rotates the order of presentation in order to control for its effects. Unfortunately, rotating the order of presentation doesn’t eliminate any of the noise from the analysis. Rather, it apportions roughly equal amounts to each cell (“prefer product A” and “prefer product B”), which makes it harder to detect a statistically significant difference when one exists. When the difference between the two products being tested is sizable, the amount of noise is likely to be negligible or nonexistent. However, when the difference between the two products being tested is small, the amount of noise can be considerable.

To make matters worse, the standard design can’t identify, and so has no way of dealing with, respondents who express a preference when they’re given two samples of the same product. As a result, these people are treated as if their preferences are driven by differences between the products. The result is more noise.

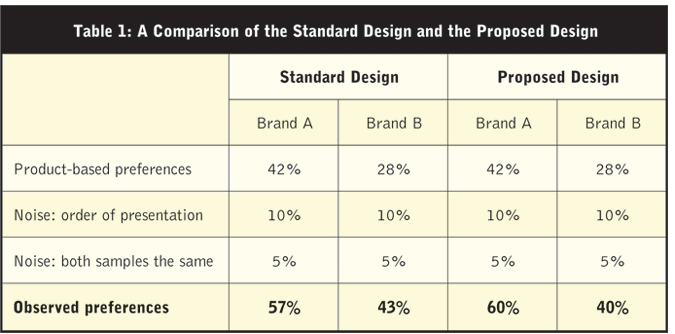
To illustrate the difference that the proposed design can make, let’s look at two scenarios (Table 1). In each, the preferences of 70 percent of the respondents are driven by the differences between the two products being tested. Another 20 percent make choices based on the order of presentation, and 10 percent express a preference - divided equally between the two brands¹ - when they’re given two samples of the same product. Among respondents whose preferences are governed by the differences between the two products being tested, 60 percent prefer Brand A. In the first scenario, the standard design is used. In the second scenario, the proposed design is used. Let’s look at the numbers.

The proposed design is able to identify and remove from the analysis respondents whose choices are determined by the order of presentation and respondents who express a preference when presented with two samples of the same product. As a result, observed levels of preference are 60 percent and 40 percent - the difference is 20 percent. In contrast, the standard design is unable to weed out the noise that’s generated by these two sources, which narrows the difference between the observed percentage that prefer Brand A and the observed percentage that prefer Brand B to 14 percent, making it more difficult to detect a statistically-significant difference when one exists.

However, the proposed design pays a price for excluding noise from the analysis. That price is a smaller sample size. For example, if both designs begin with 200 respondents, the standard design would use the entire sample to determine if the difference between 57 percent and 43 percent is significant. In contrast, the proposed design would base its comparison of 60 percent and 40 percent on a sample of 140. Since power is, in part, a function of sample size, this design loses some of its power. Indeed, the smaller the sample when the study begins and the larger the percentage of respondents that is excluded from the analysis, the less power the proposed design will have.

If a substantial percentage of respondents are excluded from the analysis, say at least 60 percent, then the difference between the two products is likely to be too small to be reliably detected, regardless of the design that’s used - which is valuable information, and the reason why the ability to measure the amount of noise is an important benefit of the proposed design. Because it’s able to identify the extent to which noise is produced, this design is able to tell us with considerable precision how noticeable the difference between the two products being tested is. The larger the sum of the following four percentages, the less noticeable this difference is likely to be:

The percentage of respondents whose choices are governed by the order of presentation but who don’t express a preference when the two samples are the same.
The percentage of respondents that express a preference when the two samples are the same but whose choices are not governed by the order of presentation.
The percentage of respondents whose choices are governed by the order of presentation and who express a preference when the two samples are the same.
The percentage of respondents that have no preference.

Going back to our hypothetical example, when respondents sampled branded Pepsi and branded Coke on the fourth trial, let’s say that 45 percent preferred Pepsi, 45 percent preferred Coke, and 10 percent had no preference. When these beverages are unbranded, let’s say that 50 percent preferred Pepsi, 30 percent preferred Coke, 10 percent had no preference, and 10 percent made choices based on the order in which the products were presented and/or expressed a preference when both samples were the same. If we exclude this 10 percent from the analysis, along with the 10 percent who had no preference, we find that 63 percent preferred Pepsi and 38 percent preferred Coke. In a head-to-head comparison, these findings tell us several important things about Coke and Pepsi:

The Pepsi formula has more power than the Coke formula.
The Pepsi formula has more power than the Pepsi brand.
The Coke brand has more power than the Coke formula.

As noted above, the larger the percentage of respondents that is excluded from the analysis, the less noticeable the difference between the two products is likely to be. Consequently, the less power either formula is likely to have. In our example, 20 percent were excluded from the analysis. Had it been 80 percent, we would be forced to conclude that most of the expressed preferences when respondents compared branded Pepsi to branded Coke were driven by the power of the brands.

At this point, we know all that we’re going to about the power of the formula. However, we can learn more about the power of each brand by conducting another test with a fresh sample of respondents.

Formula constant

This test is conducted by holding the formula constant and varying the brand, which enables us to determine the power of each brand when there is no difference between the formulas. There are four trials, with each respondent randomly assigned to one of these trials and participating only in that trial:

1. In the first trial, respondents sample Pepsi twice, but are told that the first sample is Pepsi and the second is Coke.

2. In the second trial, respondents sample Pepsi twice, but are told that the first sample is Coke and the second is Pepsi.

3. In the third trial, respondents sample Coke twice, but are told that the first sample is Pepsi and the second is Coke.

4. In the fourth trial, respondents sample Coke twice, but are told that the first sample is Coke and the second is Pepsi.

The benchmark to which these preferences are compared is 0 percent. We use 0 percent because each brand has to overcome the absence of a difference between formulas, making this an unusually demanding test. The upper limit of this range is the percentage that preferred each of these brands when respondents sampled branded Pepsi and branded Coke. Using this test, the closer the preferences for a product come to this upper limit, the more power the brand for that product has.

Fresh insights

In conclusion, the information that these tests yield about the power of a product’s formula and the power of its brand in head-to-head competition with a key competitor can provide fresh insights into the reasons for its performance, insights that can make a considerable difference in how effectively the product is marketed.

Notes

1 Although we would expect these choices to divide equally, that won’t always be the case. When it’s not, it will erroneously narrow or widen the gap between the products being tested.