Editor's note: Jay Wu is an independent consultant.
If you ask marketing researchers what advanced research tools they actually use, not those they would dust off to put in use someday, chances are that discrete choice models (DCMs) will get picked. The reason: DCM combines multivariate complexity and realistic simulation of mundane shopping experiences. In a typical DCM, each respondent is presented with multiple cards that list major alternatives or brands that are seen or will be seen in market, with varying prices and other attributes. On each card, respondents are instructed to pick one model or brand (or to allocate proportions of brands to be picked out of their next, say, 10 or 20 shopping occasions), as well as the purchase intents for the brands picked. In such a trade-off setting, consumers reveal their true preferences.
Why monadic choice cards?
One of the defining features of DCM is an experimental design, at least for DCMs dedicated to stated preferences1. The fact that each respondent reacts to multiple choice cards is both a blessing and a curse. Researchers like this feature because multiple cards open up a bigger window to better understand consumers' often complex purchasing behaviors. In this aspect, marketing researchers are not much different from law enforcement authorities, who keep 10 fingerprints for each person: when one is in doubt, the others can be compared to eliminate identification uncertainty. It is widely accepted that multiple choice cards can reduce random errors in assessing consumers' preferences under various market conditions.
However, multiple cards inevitably elongate surveys and impose a bigger mental toll on respondents than simple surveys. Studies (Johnson and Orme, 1990) have shown that beyond a certain number (up to 20 cards), the more attributes included in the design the lower response quality. Further, in analyzing data from discrete choices we commonly ignore the fact that repeated measures are obtained from the same respondent. However, even though we can advise respondents to focus on each individual card without referring back and forth to any other cards, it is unlikely that responses by the same respondent are totally independent. This puts a question mark on how reliable our choice data really are, despite the well-documented superiority of trade-off data in comparison to ordinary survey data (Louviere et al., 1990; Louviere & Woodworth, 1983).
Years of marketing research experience in general, and new product forecasts in particular, suggest to us the importance of combining the best of two worlds - trade-off exercises and straightforward surveys - in generating market insights and improving accuracy of forecasts. In this regard, we have found monadic card data to be a valuable piece of total data influx for forecasts.
Several aspects of monadic cards are just like ordinary survey items:
- no repeated measurements - unlike regular DCM cards, each respondent typically sees just one scenario, thus the name "monadic";
- no experimental design - monadic cards are designed to be a snapshot of market conditions, not a full simulator of all possible scenarios; and
- straightforward and fitting squarely into the logical flow of the survey - as a result, monadic cards can be presented at the early stage of surveys, preceding regular DCM cards.
Yet monadic cards also share features with full-fledged DCM cards:
- trade-off pressure is present when we ask respondents to pick just one brand, one product, or one service option out of many;
- respondents are stimulated by the same concept exposure used for regular DCM cards;
- the options listed on monadic cards are typically compatible to regular DCM cards; and
- the attributes and their value levels are also typically similar to regular DCM.
Monadic cards occupy a unique place in all trade-off exercises for three reasons.
First, a monadic card can be devised to resemble current or most likely market conditions for the products in question, ranging from toothbrushes to high-definition TV sets. Take price as an example: those listed on monadic cards could reflect what most consumers would likely encounter in most marketplaces either today or one, five, or 10 years down the road, while regular choice cards may convey prices randomly determined within predetermined ranges.
Second, a monadic card may be either more complete or more focused than regular choice cards in its list of models or brands2. For example, models/brands expected to phase out in the future will not be listed on a regular choice card for forecasting purposes, but may still be on a monadic card designed to reflect today's market. On the other hand, regular choice cards may sometimes show more models, anticipating future line extensions either by clients and/or by competitors, while monadic cards may choose to focus on today's major competing brands that jointly account for no less than 80 percent of market shares.
Finally, because of their positions in the flow of the survey, monadic cards typically command more of respondents' attention and thus help reduce some random errors.
Usages of monadic cards
Monadic cards have been used in practice as:
- "Shelf exposure" cards, where monadic cards deliberately simulate market scenarios today or tomorrow in order to get a direct read on specific demands under those conditions, the latter is then subject to calibration before being utilized in forecasts.
- "Design demo" cards, where monadic cards themselves are used as a demonstration of new product concepts, with details about the price and/or design features. However, monadic cards not only describe new concepts, but immediately solicit consumer responses to the concepts.
- "Holdout" cards, where monadic cards may be used to check on the predictive validity of the models and utilities derived from regular choice scenarios.
- "Sample correction" cards, where shares of preferences from monadic cards are compared with actual market shares to obtain a sense of how closely the sample at hand is representative of consumer populations and markets.
- "Add-on" cards to a hybrid design, where monadic cards depict a choice environment just like a regular choice card, so we can assess sources of volume, while the focus of the project is a conjoint exercise for an optimal product design.
- "Replacement" cards, where they are used to replace multiple choice cards when researchers are pressed with time and budget constraints. This last use is relatively rare and perhaps less defendable.
Shelf exposure cards - This usage requires that we design monadic cards in a separate process, not to be mixed and mingled with regular choice cards. While the latter are pulled out of a random process from running automated computer procedures (e.g., in SAS or SPSS), the former may involve sometimes lengthy discussions/negotiations with your clients regarding which levels, which attributes, and which alternatives (e.g., brands, models, SKUs) provide the best snapshots of market conditions. Further, it is likely these monadic cards were first drafted by hand and then given to the graphics department for tuning up and final polish before being mass produced for field execution.
Evaluating the designs requires different criteria for regular than for monadic cards. With regular cards, the objective is to fully span the experimental space with the fewest cards possible, a criterion called efficiency. This amounts to including some anchoring levels of experimental factors (i.e., attributes, brands, prices) and coming up with the best combinations of factor levels - best in the sense that our parameter estimates have the least amount of variance-covariance. With monadic cards, the objective is to achieve a "bull's-eye" hit on a specific market condition that allows a targeted read of market demands. The design of monadic cards emphasizes simulation or resemblance of market rather than efficiency, as only a few cards are involved to begin with3.
Shelf exposure monadic cards should not replace concept exposure, especially when new products with little publicity and zero public awareness are introduced. Concept exposures bring respondents up to speed with new products, and hatch a parallel awareness level between new and existing brands, for example.
Design demo cards - Used in this setting, monadic cards are very similar to cards in a conjoint exercise: a single concept is introduced on each card detailing its key features. Although different concept cards can be designed to show potentially different SKUs of the same new product, each respondent typically views just one such card, leaving different SKUs to regular conjoint cards.
The design calls for industry expertise and knowledge of the new product. Therefore, your best bet would be to consult your clients before laying out features on the card. As is typical with monadic cards, design demo cards are not generated randomly, but deliberately by asking client which levels are "most typical" for the new product.
Holdout cards - Holdouts are choice cards presented to respondents but not used in the model. Instead, the observed shares of preferences are recorded and compared with expected preferences derived from model utilities. Like shelf exposure cards, the design of holdouts is also separated from regular choice cards to ensure an independent check on predictive validity.
When used appropriately, these monadic holdout cards can be useful for improving forecasts on share of preferences. For example, if 15 percent picked Brand A from monadic holdout cards, and the expected frequencies from choice cards were also about 15 percent, we gain more confidence with the model.
Unlike shelf exposure cards, monadic holdout cards can be derived from an independent experimental design, and can contain any combinations of attributes and levels, as long as the levels are within the same range as the regular choice cards. Thus if the lowest price on the regular cards was $150 for all DVD players, you don't want to design your holdouts to contain a player with a price tag of $100. If you go out of the boundaries, model checking becomes a process of extrapolation, with a lower hit rate than intrapolation. Further, more than one monadic card is typically needed to convince yourself that the hit rates are not based on pure luck.
If the design size or the number of cards turns out to be an issue, sometimes you may make a better use of both by specifying attribute levels resembling shelf exposure. That way, you can hit two birds (shelf exposure and holdouts) with one stone. To do so, however, you have to surrender the randomization principle, as pure chance won't guarantee cards with pre-determined attribute levels for shelf exposure purpose.
Sample correction cards - If monadic cards are configured to closely resemble current market conditions, then at aggregate, monadic picks should bear similarity to current market shares. Along the same line, monadic cards can be designed to reflect the "most likely" scenarios in a perceivable future, and provide a read of how the future market landscape will look.
It is rare to use monadic cards solely for correcting samples, as monadic cards have their best place in trade-off exercises assessing consumer preferences. This usage can use the same design as for shelf exposure. However, sample correction cards should only cater to options currently available, as "new to the world" options tend to distort pictures of the current market.
Add-on cards - We practitioners all know too well that sometimes we try to hit two or more birds with one stone. For example, it's not uncommon for your clients to come to you for two things at the same time: bundling the best attributes together for an optimal design, and figuring out potential sources of volume after market introduction. In an ideal world, this case requires two studies or two modules: a conjoint exercise focusing on the optimal design, and a DCM predicting sources of volume. However, time and budget constraints are not on your side and you have to come up with a "conditional" or "constraint" optimal research design. Monadic choice cards may prove useful here.
Unlike a full-fledged DCM, respondents do not go through 10 or 20 choice cards. Instead, a couple of monadic cards featuring the low and high prices are presented, for example. Unlike conjoint cards, which focus on a single product or model or brand, monadic cards list all current or potential competitors on each card, so the respondents won't be misled into assuming the test product is the only game in town. Combining monadic and conjoint cards, you should be able to tell your client a story both about the source of volumes (from the monadic cards) and about the best bundling strategy (from a conjoint exercise) - without breaking the bank.
Replacement cards - This is a problematic usage of monadic cards. In all situations discussed above, monadic cards are supplementary to either regular choice cards or conjoint cards. Here however monadic cards are used solo, in place of a full-fledged DCM. To see why we cannot mix the two, we move to a discussion of problems and limits with monadic cards.
Weaknesses of monadic choice cards
Just because monadic cards are designed to replicate market scenarios does not automatically guarantee a reading of true share of preference. In fact, because only one scenario is presented, one risks over-generalization of a chance response or a random pick out of low involvement, low motivation, ill-preparation, or even bias towards a respondent's last shopping experience, whichever brands or models he or she happened to pick. It is in this sense that we discourage "standalone" or solo use of monadic cards. Unless circumstances rule out other options, projects that totally rely on monadic cards should not be viewed as viable.
Although one may argue, as we did above, that monadic cards typically receive more respondent attention than some of regular choice cards towards the end of a DCM exercise, the early position of monadic cards in the survey flow may also invite problems. For example, some practitioners have been heeding the academic advice to add one or two "warm-up" cards in places where a monadic card is expected, in order to prepare respondents for the task of making hypothetical choices. Those warm-up cards are not analyzed in models due to the concern they may contain more noise than data. Although evidence suggests that usage of warm-up cards has never been a mainstay, given the time and budget constraints of real-life projects, it does underscore the concern that all choice cards are not equal: responses to the first few cards may result in garbage inputs. This is exactly where a process of information acceleration is called upon, as discussed later.
As a final caution, your clients may have placed too much emphasis on the monadic card results, sometimes simply because they are as intuitive as any survey items, while regular DCM results are less transparent. Emotions may run high because these scenarios mirror clients' strongest belief as to how the current or future markets will look. It is the analyst's responsibility to educate clients that the objective of DCM exercises is to generate utilities - which are then used to estimate shares of preferences to be used for forecasting consumer demand - not to bid on any single choice card exclusively. Our hope is to work with multiple choice cards to arrive at reliable and accurate utility estimates. Once we have utilities, we can easily come up with various simulations, including those that are believed to be most likely scenarios.
On a more general note, DCM analyses typically are based on three aggregations - aggregating across respondents (that is, we obtain utilities for the entire sample or segments of sample, not for individual respondents) aggregating over attributes (that is, at the end of the analysis, we often come to a conclusion about which models or brands take on how many respondents, not about which attribute levels [e.g., a specific price or a brand name] appeal most to people, although the latter is an important intermittent result and can be used to address separate concerns if needed), and aggregating over scenarios or cards (that is, we care less about how respondents react to a specific card than about how alternatives are preferred overall, across all cards).
Ways of utilizing monadic choice data
Perhaps the simplest way of utilizing monadic cards is to record proportions of picks for each alternative. For example, from a monadic card 15 percent of the sample picked Brand A, 45 percent Brand B, 30 percent Brand C and 10 percent none. These observed proportions are then used directly in gauging market demands and calibrating the forecasted figures. Using observed proportions of picks from monadic cards is especially appropriate for a holdout function. It has the advantage of simplicity and is analytically friendly.
The best practice in utilizing monadic cards in forecasts should include two features. First, concept demonstrations of new products should be presented prior to monadic cards to better prepare respondents to the trade-off task. This is part of what Urban & Hauser (1983) called "information acceleration" processes. Second, since observed picks contain random errors, analytically it makes sense to estimate utilities from monadic data just like we do with regular choice scenarios. By subjecting monadic choice data to the scrutiny of statistical models, one obtains utilities - which are similar to the predicted values in a regression model - of each attribute and each model/brand, and puts monadic data on a par with the rest of choice data, rendering more reliable benchmarks information for forecasting.
Most trade-off analysts are familiar with modeling multiple choice cards. This practice is so prevalent that multi-card modeling may have been mistakenly viewed as equivalent to DCM. However, suffice it to mention that economists have been using single observed choice data to generate utilities all the time. In fact, we have witnessed a long history of DCMs with revealed preferences. (e.g., Ben-Akiva & Lerman, 1985). We will present a real-life example showing how to estimate utilities from monadic cards. However, some general discussion of issues with using monadic choice cards is due first.
Analyzing monadic choice data: what is at stake?
Analyzing monadic choice data requires some customization. As pointed out earlier, monadic cards are typically not part of random designs. We thus do not have the luxury of packaged procedures to work with, and have to take manual and customized steps.
The major steps involved are to 1) translate monadic cards into an array of attributes, 2) set up a design using these attributes, 3) read in the monadic responses, 4) merge design variables with responses or picks to a dataset ready for analysis, and finally 5) estimate utilities. You may opt to add an extra step for checking goodness of fit of the monadic models. The pivotal part of this process is to set up a post hoc experiment design file as if the monadic cards were generated from such a design.
As far as software is concerned for analyzing regular and monadic choice data, our favorite is SAS, which has powerful procedures like PROC FACTEX, PROC PLAN, and PROC OPTEX that address your design needs well and create efficient designs. For analytic purposes, SAS uses two procedures: PROC TRANSREG sets up data and PROC PHREG estimates utilities. In the sample analysis below, we present SAS codes for completing an analysis from start to finish.
A real-life example
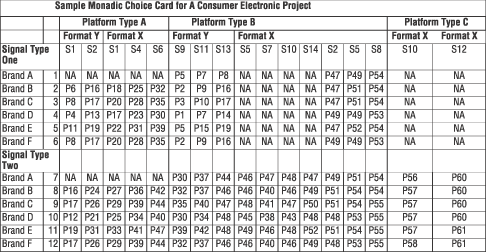
The card and the design. Table 1 shows a monadic card for jumbo TV sets. The card itself is "jumbo" in the number of possible choices. Each cell in the grid denotes a unique choice for respondents to pick, and there are 12 rows and 17 columns, making a total of 12 x 17 = 204 possible cells, of which 46 were marked "N/A" due to unavailability of certain brands at certain sizes (e.g., Brand A for all PLATFORM As; all brands for Screen Format X with Signal Type I,) thus reducing the number of non-missing cells to 158.
 |
Eyeballing of the card points to five experimental factors: technological platforms (Platforms A, B, and C), screen formats (Formats X and Y), signal types (Signals 1 and 2), brands (with faceless names from Brand A to Brand F for client confidentiality), and screen sizes (ranging from S1 to S14).
The following codes are written with the above monadic card in mind:
- proc format;
value signalf 1="Signal 1" 2="Signal 2";
value platformf 1="A" 2="B" 3="C";
value scrnformf 1="Y" 2="X";
value sizef 1="S1" 2="S2" 3="S3" 4="S4" 5="S5" 6="S6" 7="S7" 8="S8" 9="S9" 10="S10"11="S11" 12="S12" 13="S13" 14="S14";
value brandsf 1="BRAND A" 2="BRAND B" 3="BRAND C" 4="BRAND D" 5="BRAND E" 6="BRAND F";
run;
*--step 1: generate all possible combinations of 5 factors--;
proc plan ordered;
factors platform=3 scrnform=2 signal=2 brands=6 sizes=14;
output out=CAND1;
run;
PROC PLAN is good for generating full factorial experimental designs, which in this case amount to 3 x 2 x 2 x 6 x 14 = 1,008 unique combinations of five attributes.
A portion of the output data, CAND1, is shown in a condensed format in Table 2.
 |
We have a total of 3 x 2 x 2 x 6 = 72 lines with the last SIZES factor folding up its 14 levels to a single line. When you expand SIZES into different lines or rows, you obtain the full design with 72 x 14 = 1,008 cases.
The fact that we started with a full factorial design marks the first difference between monadic and regular choice cards. For the latter of the same size as the monadic card shown above, we would often use a fractional factorial design generated by PROC FACTEX because we want to let randomization play its role to generate the best combinations of attributes or factors across multiple cards. Monadic cards, however, contain pre-determined attribute levels; there is thus no place for randomization. We are merely using PROC PLAN to generate an exhaustive list of all possible combinations of numbers to be trimmed down to what is actually shown on the monadic cards. The vast majority in CAND1 will have to go away as they do not resemble what the respondents actually have been exposed to.
Our next step is to cut down 1,008 values to 158:
- *--step 2: matching the number of cells on monadic card--;
data CAND2;
set CAND1;
if (platform=1 and scrnform=1 and sizes in(2,4) and brands ne 1) or
(platform=1 and scrnform=2 and sizes in(1,3,6) and brands ne 1) or
(platform=2 and scrnform=1 and sizes in(9,11,13)) or
(platform=2 and scrnform=2 and signal=2 and sizes in(5,7,10,14)) or
(platform=3 and scrnform=2 and signal=1 and sizes in(2,5,8)) or
(platform=3 and scrnform=2 and signal=2 and sizes in(2,5,8,10,12));
run;
The IF statement with a list of target conditions selects the combinations consistent with the monadic card. The CAND2 dataset now has 158 cases. We list the first 10 observations in Table 3.
 |
One key element missing from CAND2 is prices. All cells in Table 1 are filled with a price. We need to do the same for our post hoc design file. While there are many ways to enter the prices, we chose to enter them all into a spreadsheet file in a comma-separated format ("MONADIC PRICES.CSV") in the order listed on the monadic card, and then merge them into the design file.
- *--step 3: read in price variable from excel--;
data PRICES;
infile 'monadic prices.csv';
input prices;
run;
*--step 4: add prices to design matrix--;
data DES_PRI;
merge CAND2 PRICES;
price_sq=prices*prices;
size=input(put(sizes,sizef.),6.0);
size_sq=size*size;
drop sizes;
run;
Dataset DES_PRI generated in Step 4 also contains price-squared and size-squared in case they may be needed to help fit the monadic data better.
The first five observations of the design file are shown in Table 4.
 |
Frequencies of monadic picks. With the design file in place, we now switch to the responses (i.e., picks) on the monadic card, which were stored in a previously created SAS file, DCM_RESPONSE.
- *--step 5:responses or picks from monadic card--;
data MONADIC;
set DCM_RESPONSE;
*--code the screen size variable--;
*--"A_X_S1" means Platform A, Screen format X, and Screen size S1; refer to Figure One for the choices--;
if A_X_S1 ne . then sizes=1;
if A_Y_S1 ne . or C_X_S1 ne . then sizes=2;
if A_X_S4 ne . then sizes=3;
if A_Y_S2 ne . then sizes=4;
if B_X_S5 ne . or C_X_S5 ne . then sizes=5;
if A_X_S6 ne . then sizes=6;
if B_X_S7 ne . then sizes=7;
if C_X_S8 ne . then sizes=8;
if B_Y_S9 ne . then sizes=9;
if B_X_S10 ne . or C_X_S10 ne . then sizes=10;
if B_Y_S11 ne . then sizes=11;
if C_X_S12 ne . then sizes=12;
if B_Y_S13 ne . then sizes=13;
if B_X_S14 ne . then sizes=14;
*--array for coding screen formats--;
array scrnf(*) A_Y_S1 A_Y_S2 B_Y_S9 B_Y_S11 B_Y_S13 A_X_S1 A_X_S4 A_X_S6 B_X_S5 B_X_S7 B_X_S10 B_X_S14 C_X_S1 C_X_S5 C_X_S8 C_X_S10 C_X_S12;
*--create screen format variable--;
do i=1 to 5;
if scrnf(i) ne . then scrnform=1; /*Screen format "Y"*/
end;
do i=6 to 17;
if scrnf(i) ne . then scrnform=2; /*Screen format "X"*/
end;
*--array for coding tech platforms, signal types, and brands--;
array rinits(*) A_Y_S1 A_Y_S2 A_X_S1 A_X_S4 A_X_S6 B_Y_S9 B_Y_S11 B_Y_S13 B_X_S5 B_X_S7 B_X_S10 B_X_S14 C_X_S1 C_X_S5 C_X_S8 C_X_S10 C_X_S12;
*--create the tech platform variable--;
do i=1 to 5;
if rinits(i) ne . then platform=1; /*Tech Platform "A"*/
end;
do i=6 to 12;
if rinits(i) ne . then platform=2; /*Tech Platform "B"*/
end;
do i=13 to 17;
if rinits(i) ne . then platform=3; /*Tech Platform "C"*/
end;
*--code signal type variable--;
do i=1 to dim(rinits);
if rinits(i) in(7,8,9,0,11,12) then signal=2; /*Signal Type 2*/
else if rinits(i) in(1,2,3,4,5,6) then signal=1; /*Signal Type 1*/
end;
*--code brands variable--;
do i=1 to dim(rinits);
if rinits(i) in(1,7) then brands=1;
else if rinits(i) in(2,8) then brands=2;
else if rinits(i) in(3,9) then brands=3;
else if rinits(i) in(4,0) then brands=4;
else if rinits(i) in(5,11) then brands=5;
else if rinits(i) in(6,12) then brands=6;
end;
drop i;
format A_Y_S1 A_Y_S2 A_XS1 A_X_S4 A_X_S6 B_Y_S9 B_Y_S11 B_Y_S13 B_X_S5 B_X_S7 B_X_S10 B_X_S14 C_X_S1 C_X_S5 C_X_S8 C_X_S10 C_X_S12 dcpick.
brands brandsf. platform platformf. sizes sizef. scrnform scrnformf. signal signalf.;
run;
Our goal is to align monadic responses (i.e., the picks) with the design file. That is, dataset MONADIC created above contains all variables (PLATFORM SIZES SCRNFORM SIGNAL BRANDS) in the design file except prices. But why do we need duplicated variables in both response dataset (i.e., MONADIC) and the design dataset (i.e., DES_PRI)? The answer is, we don't. The only reason we have them there in MONADIC is that so we can create frequencies of picks for all cells on the monadic card, which is derived from jointing those five design variables.
The following PROC FREQ counts how many respondents picked which options out of the monadic card:
- *--step 6: get freq for each alternative in monadic card--;
proc freq data=MONADIC noprint;
tables platform*scrnform*signal*brands*sizes /out=CC(drop=percent);
run;
The output dataset CC contains frequencies falling into the "N/A" cells on the monadic card, where there should be none. We run another data step to clean up the data.
- *--step 7: delete illegal responses--;
data NCC;
set CC;
*--delete responses that are not part of design--;
if platform=2 and scrnform=2 and signal=1 then delete;
*--delete aggregated frequency--;
if platform=. and scrnform=. and signal=. and brands=. and sizes=. then delete;
run;
The first 10 observations of NCC are listed in Table 5. There were, for example, eight respondents picking the first non-missing cell, and five for the next cell.
 |
Merging design with monadic responses. This is one of the key steps: merging the frequencies of picks with the design file:
- *--step 8: merge response with design--;
data READY;
merge DES_PRI NCC;
by platform scrnform signal brands size; /*merge by all five factors to ensure exact match*/
*--two lines output for each case in NCC, creating a censoring variable required by PROC PHREG--;
freq=count;
c=1; /*censoring variable*/
output;
freq=752-freq;
*--if no price listed frequency is 0--;
if prices=0 and freq=752 then freq=0;
c=2; /*censoring variable*/
output;
drop count;
run;
PROC PHREG, which we use to analyze monadic choices, requires a censoring factor (called "C" in our code above) with a value of "1" denoting frequencies of picks and "2" for non picks (PHREG was originally designed for survival analysis, in which censored variables play a crucial role in models). Thus for the first non-missing cell, the eight respondents falling into this specific cell have a value of "1" on variable C, while 752 - 8 = 744 cases have a value of "2" for not picking this specific choice (the total sample size for this study was 752). This step doubles the number of observations in dataset READY shown in Table 6 for the first six cases.
 |
Coding main and interaction effects for the model. Dataset READY is in a shape ready for PROC TRANSREG, which creates all main effects, all linear effects, and interaction or cross effects between PLATFORM, SCRNFORM and prices.
- *--step 9: set up data for PHREG, adding cross effects--;
proc transreg data=ready design=2000 noz nor;
model class(brands platform scrnform signal /zero=none)
identity(size size_sq prices)
class(platform scrnform /zero=none)*identity(prices)/lprefix=0;
output out=CODED(drop=_type_ _name_ intercept);
id c freq;
label prices='Prices' platform='Platform' scrnform='Screen format' signal='Signal Type'
size='Screen size' size_sq='Size Squared';
run;
With PROC TRANSREG, linear effects are created with an IDENTITY statement, while the ANOVA-type main effects are coded with a CLASS statement for classification factors (the option "ZERO=NONE" in the CLASS statement asks for no explicit zeros, thus the last level of each factor will act as the reference level, with a "0" value of estimated parameter). To find out whether different platforms and screen formats have different price elasticities, the statement:
- CLASS(Platform Scrnform /Zero=None)*IDENTITY(PRICES)
creates an interaction between the two CLASS variables, PLATFORM and SCRNFORM, and prices.
Modeling monadic picks. The total number of variables in the output dataset CODED from PROC TRANSREG is now 27 instead of 10 as in dataset READY. Most of them have a binary coding with values of "1" and "0", suiting the need for PROC PHREG.
- *--step 10: analyze the model--;
proc phreg data=coded outest=betas nosummary;
model c*c(2)= &_trgind /ties=breslow;
freq freq;
title "DCM for Monadic Data";
run;
PROC TRANSREG saves much time on coding model effects. Once you have run it, your code for PROC PHREG will be quite succinct. For example, instead of citing all the effects on the right hand of the MODEL statement, you simply put "&_trgind" there, which is a macro variable containing all coded effects, both main and interactions4.
After submitting the above code, we obtain the output shown in Table 7.
 |
We see that Brand E is the most preferred brand, followed by A, B, F, D, and C. For platforms, C is the most preferred one, followed by A then B. For screen formats, Y is preferred to X. For signal types, Signal 2 is preferred to Signal 1. Further, larger screen sizes and lower prices are preferred. Looking at the interactions, we observe that although Platform C had an edge over Platforms A and B, the latter two had a positive price interaction, implying that respondents may have used price as a quality proxy and thus as the price moves up, we may see more picks of those platforms. This is true especially for Platform B, whose price interaction was significant. On the other hand, of the two screen formats, Y had a positive main effect compared to X, but its price interaction was significantly negative, meaning that consumers may not tolerate a high price tag for Screen Format Y. Setting too high a price would hurt its share. Finally, we see that Platform A's price interaction was not significant (Pr>0.606). At this point we may opt to delete that specific effect and re-fit the model.
Assessing goodness of fit. Having just one card makes it easier to compare the expected and the observed picks to assess goodness of model fit5. The following steps are taken to achieve that goal.
First we need to multiply multinomial logit model parameters with design values to produce predicted values. Although there are many ways of doing it, the most elegant and yet convenient is to use SAS PROC SCORE, which yields a new variable we call "XB",
Ÿ = ∑i ∑j Xij1 ßj
where "i" denotes respondents and "j" design factors.
As the model parameters are on a log scale, XB really denotes log predicted values, which are then anti-log transformed through another data step.
- *--step 11: log utilities--;
proc score data=coded(drop=c) score=betas type=parms
out=p(keep=platform scrnform signal size size_sq prices brands freq c rename=(c=xb));
var &_trgind;
run;
Dataset CODED was created from PROC TRANSREG and used in PROC PHREG. It is used again as input for PROC SCORE. Because of its origin from PROC TRANSREG, the automatic macro variable &_TRGIND is still active to be used here in PROC SCORE.
The first 10 cases from output dataset P are shown in Table 8.
 |
All attributes from the design file are listed first, followed by XB. At this step, we have not deleted duplicated values due to the censoring variable C having two values. Therefore, each unique combination of attributes is repeated twice. This problem is fixed next.
- *--step 12: removing duplicated utilities, computing exponential utilities--;
data p2;
set p;
if mod(_n_,2) ne 0; /*cut off duplicated utilities caused by censoring variable C*/
exb= exp(xb); /*exponential utilities*/
run;
Using predicted values we next compute shares of preference for each cell on the monadic card. First we obtain the total utility across all attributes, which is to be used as the denominator for computing expected picks.
- *--step 13: sum of exp utilities--;
proc means data=p2 noprint;
output out=S sum(exb) = t_exb;
run;
Dataset S contains just one line of data - the sum of exponential utilities. Next we compute share of preferences for all combinations of design factors (i.e., all 158 choices listed on the monadic card).
- *--step 14: share of preferences--;
data p3;
if _n_=1 then set s;
set p2;
e_sop=exb/t_exb; /*expected share of preference*/
exp_freq=e_sop*752; /*expected picks*/
run;
Table 9 shows the first 10 cells on the monadic card showing both observed picks (FREQ) and that based on model utilities (EXP_FREQ).
 |
With expected and observed picks, we run a simple linear regression model using observed picks as dependent and expected picks as independent variables.
- proc reg data=p3;
model freq=exp_freq;
run;
The ANOVA result is shown in Table 10.
 |
The model has successfully explained almost 80 percent (77 percent) of the observed picks.
Conclusion
This article discussed usage of monadic cards in forecasting consumer demands and consumer preferences. It demonstrated one way of analyzing monadic data to estimate utilities, using a real-life forecasting project in consumer electronics. We showed that even large monadic cards with about 160 valid cells can be analyzed successfully.
NOTES
1 Most DCM projects in marketing research handle stated preferences: we put respondents in hypothetical yet realistic shopping situations and they state which models, brands, or products they prefer most in each situation. Economists often conduct studies for revealed preference, in which people's behaviors are observed in a field setting rather than asked and stated. This latter type does not require repeated measures from the same individual. We focus on stated preferences in this article.
2 Monadic cards with a different set of alternatives from regular cards, however, may render the two less comparable. If the purpose of monadic cards is to provide benchmarks to help calibrate trade-off results, one should reduce the dissimilarity with regular choice scenarios to the extent possible. Of course, extracting utilities from monadic cards - as this article is focused on - should enhance comparability with regular choice scenarios.
3 Multiple monadic cards are needed when multi-year forecasts are desired (e.g., forecasting sales in the years of 2003, 2005, and 2010). Either a between- or a within-subject design is feasible, depending on sample sizes, design sizes (i.e., how many regular choice cards for each year to be forecasted), and length of survey. A between-subject design amounts to dividing the sample into cells or groups, with different cells viewing different monadic cards for different years. A within-subject design calls for each respondent to view several monadic cards, and to make a pick from within each scenario.
4 If some cross effects turn out insignificant, you can use the following trick: add a line "%put &_trgind;" immediately after PROC TRANSREG, which puts all the model effects to the LOG window. You can then cut and paste those effects to be part of PROC PHREG code, replacing MODEL C*C(2)=&_TRGIND with a long list of effects.
5 Although technically feasible, the author is not aware of any goodness of fit diagnosis for regular choice data. Again, this is at least partly due to the fact that our focus is not on any single card of data, but the pattern of responses across several cards.
References for further reading
Ben-Akiva, M. and Lerman, S. R., Discrete Choice Analysis: Theory and Application to Travel Demand, The MIT Press, 1985
Johnson, R. M. and Orme, B. K., "How Many Questions Should You Ask In Choice-Based Conjoint Studies?" ART Forum, Beaver Creek, 1996
Louviere, J. J., Anderson, D., White, J. B., and Eagle, T. C., "Predicting Preferences for New Product Configurations: A High Tech Example", in Carnevale, M, Lucertini, M. and Nicosia, S (Ed.) Modeling the Innovation (North Holland, 1990)
Louviere, J. J. and Woodworth, G., "Design and analysis of simulated consumer choice or allocation experiments: an approach based on aggregated data," Journal of Marketing Research 20(1983) 350-367
Urban, G. L. and Hauser, J., Design and Marketing of New Products, Prentice Hall, 1993