Editor’s note: Thomas Murphy is senior consultant, advanced analytics, at the Minneapolis office of San Francisco research firm MarketTools Inc.
As part of the process of planning product improvements or introducing new products, marketers often consider long lists of features for inclusion. As researchers, we regularly get requests, particularly by marketers in the technology sector, for lists of product features ranked in descending order of customer preference. Our clients also want to know the relative strength of features and like to see a “strength score” for each. Quite often our clients have extensive lists, numbering 70 features or more.
In the past we have provided results in descending order of preference so that product development teams can set their product requirements, feature lists and release plans. Alternative analyses may be rejected because product managers and developers like to have lists sorted by priority.
Most often a Bradley-Terry analysis would fit their needs, giving them a list of 70 scores corresponding to the features’ relative strength. The client could then sort product features from high to low. It is a seemingly simple approach, except that ranking 70 items can cause respondent fatigue and result in data-quality concerns. Also, 70 items can make the implementation of a Bradley-Terry analysis problematic. This article explores different ways of implementing Bradley-Terry for large lists and proposes an optimal solution.
A Bradley-Terry analysis uses ranking data to assign each feature a score, known as the BT score. These scores can then be scaled so that they add up to 100 for ease of use. In addition, the scores represent probability, so one can determine how often one feature is preferred over another.
This analysis is an often-used technique because it is relatively simple (and therefore inexpensive) to create a list of items with a relative-strength score attached. These lists can be used in many different ways.
For example, say the client wishes to rank five features of a software product to determine which features to add in what order: scalability, strong life cycle support, delivers good return on investment, multimodality and strong self-service capabilities.
The respondents are asked to rank the features by importance from 1 to 5, and a Bradley-Terry analysis is run. Say the results are as follows:
Feature BT Score
Scalability 50
Strong life cycle support 20
Delivers good ROI 15
Multimodality 10
Strong self-service capabilities 5
This gives a descending list of preferences with a relative strength attached. The scores represent probabilities with which one can determine how often one feature would be picked in relation to another. For example, out of 70 respondents in this case, 50 would rank scalability over strong life cycle support. The probability that one feature outranks another is found by dividing a score by the sum of two scores of the benefits being considered. For scalability versus strong life cycle support, the probability that scalability is preferred is 50 / (50 + 20), which is about 71 percent.
Statistical significance is difficult to determine, as it is in derived weights. A good rule of thumb is that when one item has a probability of 60 percent of being preferred over another item, it is starting to become strong. “Delivers good ROI,” with a Bradley-Terry score of 15, and multimodality at 10 is an example of this 60 percent: 15 / (15 + 10) = 0.60, so “delivers good ROI” meets this criterion over multimodality.
A Bradley-Terry analysis can be run on various software platforms. It’s simple enough that the analysis can be done using Excel. There are two steps: 1) create a win/loss matrix in which items are the rows and the columns and each cell of the matrix represents how often (percentage) the column item outranks the row; 2) project a two-dimensional matrix down to one dimension giving the BT scores.
Some effort
Despite its usefulness, the main issue with implementing Bradley-Terry analysis is that it requires some effort by the respondent. Bradley-Terry forces the respondent to rank items, a potentially strenuous task. Moreover, if the number of items to be ranked is large, it could be a nearly impossible task.
Another issue is the number of items that a respondent can accurately rank. Can a respondent accurately rank 20 or 30 items? Or is 10 a better number? The top end and the bottom end will, most likely, be pretty accurate, but what about the middle? What if there are 30 items?
A common way of dealing with this is to have the respondent rank the top several of a long list, such as the top eight in a list of 30 items, leaving the rest blank. In terms of analysis, these blanks are considered to have a rank of nine, so they are outranked by items one through eight and tied with the others with a rank of nine (the other blanks). This isn’t a true Bradley-Terry, as all items should be ranked, but it is probably more accurate than asking the respondent to rank all 30 items and is a common technique.
This approach becomes more problematic as the number of items increases. What if there are 70 items? Asking the respondent to rank the top 10 of 70 means he or she is ranking only one-seventh of the items and must pore over a list of 70 - a strenuous (or most likely impossible) task. For both these reasons, the resulting BT scores are suspect. One could try to mitigate this by doing the bottom 10 as well as the top 10.
Another technique is to have the respondent rank a random 10. (Bradley-Terry handles missing values.) This method requires only one ranking of 10 items and theoretically should work well. Unlike the previously discussed methods, however, respondents tend to rank many items in the middle of the list and will most likely have more issues with this as opposed to ranking items on the top or bottom of the list or picking the most-liked or -disliked from a list. In addition, the data are missing, which could prove problematic in subanalyses. Also, some clients are suspicious of this method; they do not like the idea of respondents randomly evaluating a subset of the attributes.
Smaller subsets
Given the facts that respondents will generally rank smaller lists of items more accurately than larger lists and that BT scores from larger lists are not truly Bradley-Terry in that respondents do not rank all the items but only the top 10 or so, an alternative is to ask respondents to rank smaller subsets of the list. These subsets should be determined randomly for each respondent.
For example, say you have a list of 70 items. Instead of having the respondent rank the top 10 of 70, pose the question like this:
Which one of the following would you rank the highest in terms of xxxxx? Which one would you rank the lowest?
Item 4
Item 26
Item 12
Item 44
Item 62
Item 23
Item 43
Now, of the following list, which would you rank the highest in terms of xxxxx? Which one would you rank the lowest?
Item 51
Item 65
Item 2
Item 61
Item 37
Item 36
Item 16
Do this eight more times so that all 70 items are reviewed. Once the respondent has ranked his or her top choice for each of the subgroups, the top-ranked choices are fed into a single ranking exercise. In the preceding example, the respondent is asked to rank these top 10 “winners.” The same is done for the bottom 10.
The data are converted to BT scores by doing the analysis on the final ranking exercise, with the items not winning in their respective subgroup given a lower ranking of 11. The bottom 10 features are coded 12 to 21.
Could be tempted
Having a respondent rank all 70 is nearly impossible. The respondent could be tempted to straightline to get through the list and/or drop out of the survey or fill it out randomly after a start. Even if the respondent were motivated and took the time, the results would probably not be very accurate, particularly the middle-ranked items. How does one judge whether one truly likes a feature as 45th or 46th?
To test various methods, 70 random numbers were generated for each respondent to represent his or her preference. In reality some items will be more popular than others, so the random numbers were generated in Excel from 0 to 35 plus 1 for item number 1, plus 2 for item number 2, plus 3 for item number 3, up to plus 70 for item number 70. This means that the later the number was randomly generated, the lower in rank it would tend to be. There is still a large variability among respondents, however. These scores are then ranked from 1 to 70, with 1 being the highest rank and 70 being the lowest. This means the “true” ranking will be close to the item number, although there will be great differences per respondent. Five hundred responses were generated.
Note that this is artificial in that there is no way to truly collect this ranking (a nearly impossible task with 70 items being ranked). Using this data, however, allows testing of various methods to see how well they do relative to the “true” ranking.
Top 10
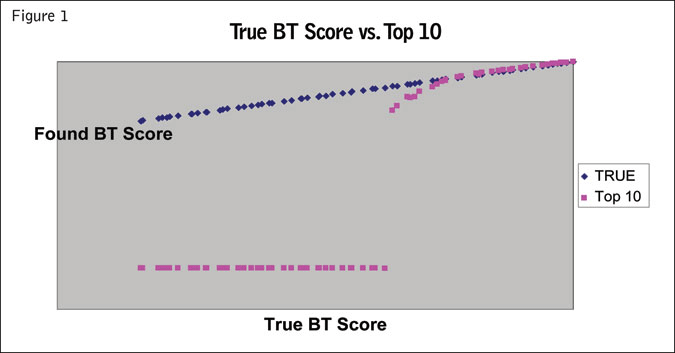
The first analysis tested is a commonly-seen top 10 approach. This is where the respondent is shown the entire list and is asked to rank the top 10. An issue here is that the list is of 70 items. As noted before, it would be difficult and taxing for the respondent to go through the list of 70. Assuming one could, however, how well would it do on the test data?
Figure 1 shows the “true” BT scores with the top 10 BT scores. Note that the 20 or so top 10 BT scores are pretty close. After that the next several start to drop. Finally, there reaches a point where the scores abruptly hit bottom. Now, for 70 items, most researchers would not do only the top 10 but also the top 20 or so. Ranking 20 is difficult on the respondent, however, so there will be some distortion. It also shows that there is a point in the middle where the scores seem to be fine (if one doesn’t have the “true” scores to compare) but actually underestimate. From this example alone, one should be concerned about using this method unless at least half the total items are ranked.
Top 10/Bottom 10
This analysis takes the foregoing top 10 analysis and combines it with a bottom 10 as well. Figure 2 shows the results. As you can see, this is a truly unacceptable method. The two analyses do not combine well. What makes this particularly problematic is that at first look the method seems logical.
Random 10
This analysis, as stated above, has the respondent rank a random 10 (of 70) items. The result is shown in Figure 3. Random 10 is very close. It should be, logically, because the data made for this exercise are considered accurate and this method picks a random 10 of them. In reality, the random 10 method has some issues, such as the respondent’s being able to accurately rank the 10 items: the respondent could be given all or most of the random 10 that would be in the middle of his or her preference, making it more difficult to accurately rank. Also, because the data have missing elements (not everyone saw everything), it is difficult to run other analyses such as factor and cluster. In addition, there could be client acceptance issues, although the method seems very sound overall.

Alternative
Figure 4 shows the alternative method mentioned previously, in which shorter, separate lists are evaluated by respondents. This is also very close. The method seems very sound. It is equivalent to the random 10 method but does not have missing data, so other analyses like factor and cluster could be done on the data.
Stronger results
If you typically use Bradley-Terry analysis to prioritize a large list of items, we recommend the random 10 or alternative method for much stronger results. We recommend these because of minimal respondent fatigue and also because they will go a lot further in guiding marketers to make successful product development decisions. The random 10 method may present issues in terms of respondents’ ability to accurately rank choices, client acceptance and the fact that not all respondents see all items (as they do with the alternative method). If these issues are of concern, the alternative method would be the better approach for researchers to employ.